最长平衡子数组 II
前置知识
该方法假定读者已经熟练掌握前缀和与线段树的相关知识与应用。
方法一:前缀和 + 线段树
本题的关键突破口是将题意中的“奇数元素种类”和“偶数元素种类”以一种量化的方式转换为数据结构可以处理的问题,具体而言,我们可以设出现一种奇数元素记为 $-1$,出现一种偶数元素记为 $1$,子数组平衡的条件即为转换后所有元素之和为 $0$。
这样转换后,易观察出我们其实得到了一个差分数组,只不过将奇数元素记为 $-1$,偶元素记为 $1$。因此对其计算前缀和,前缀和为 $0$ 时说明对应前缀子数组是平衡的。因此在固定左边界的情况下,最长的平衡子数组的右边界即为该前缀和中最后一个 $0$ 所在的位置。
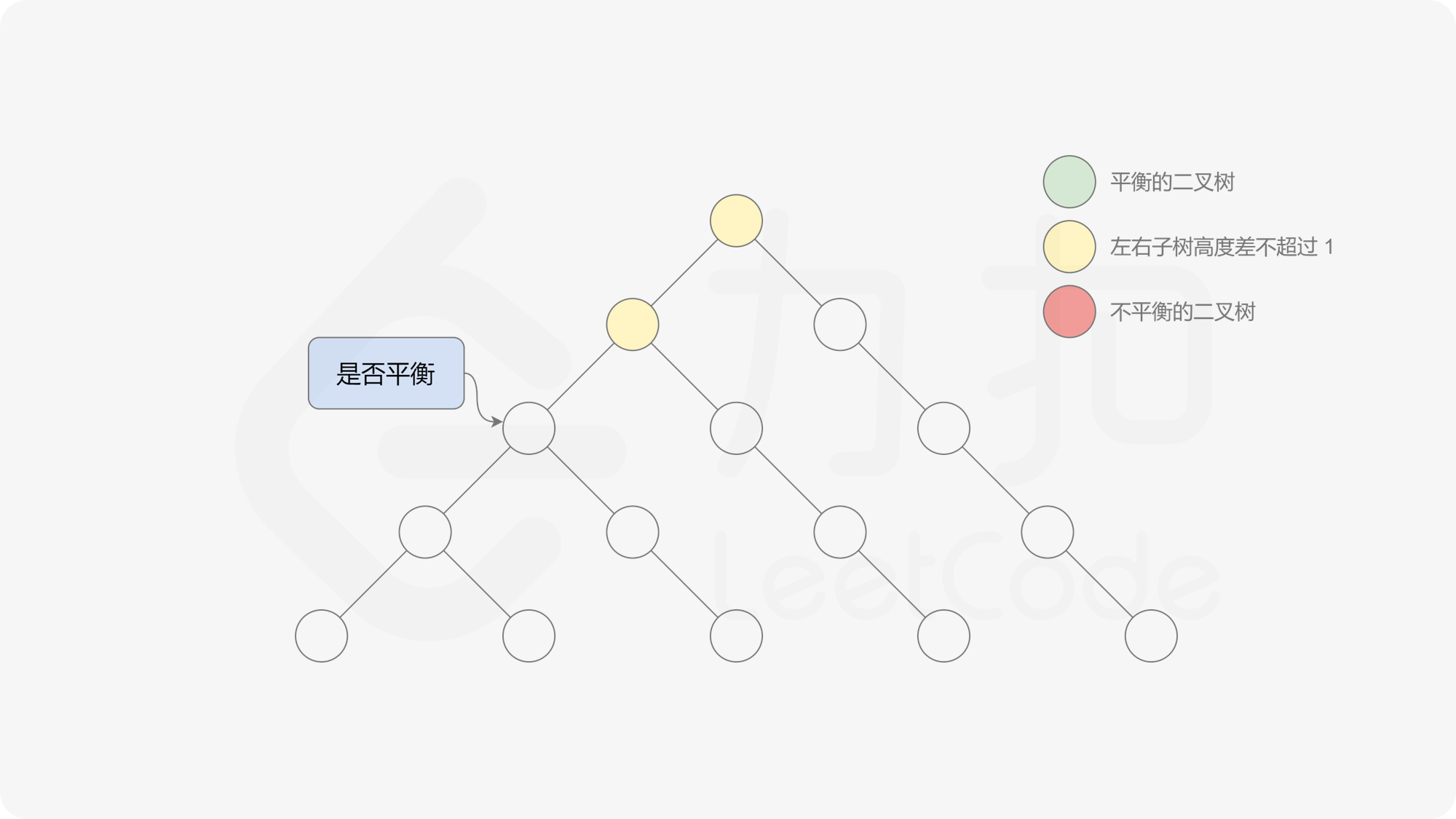
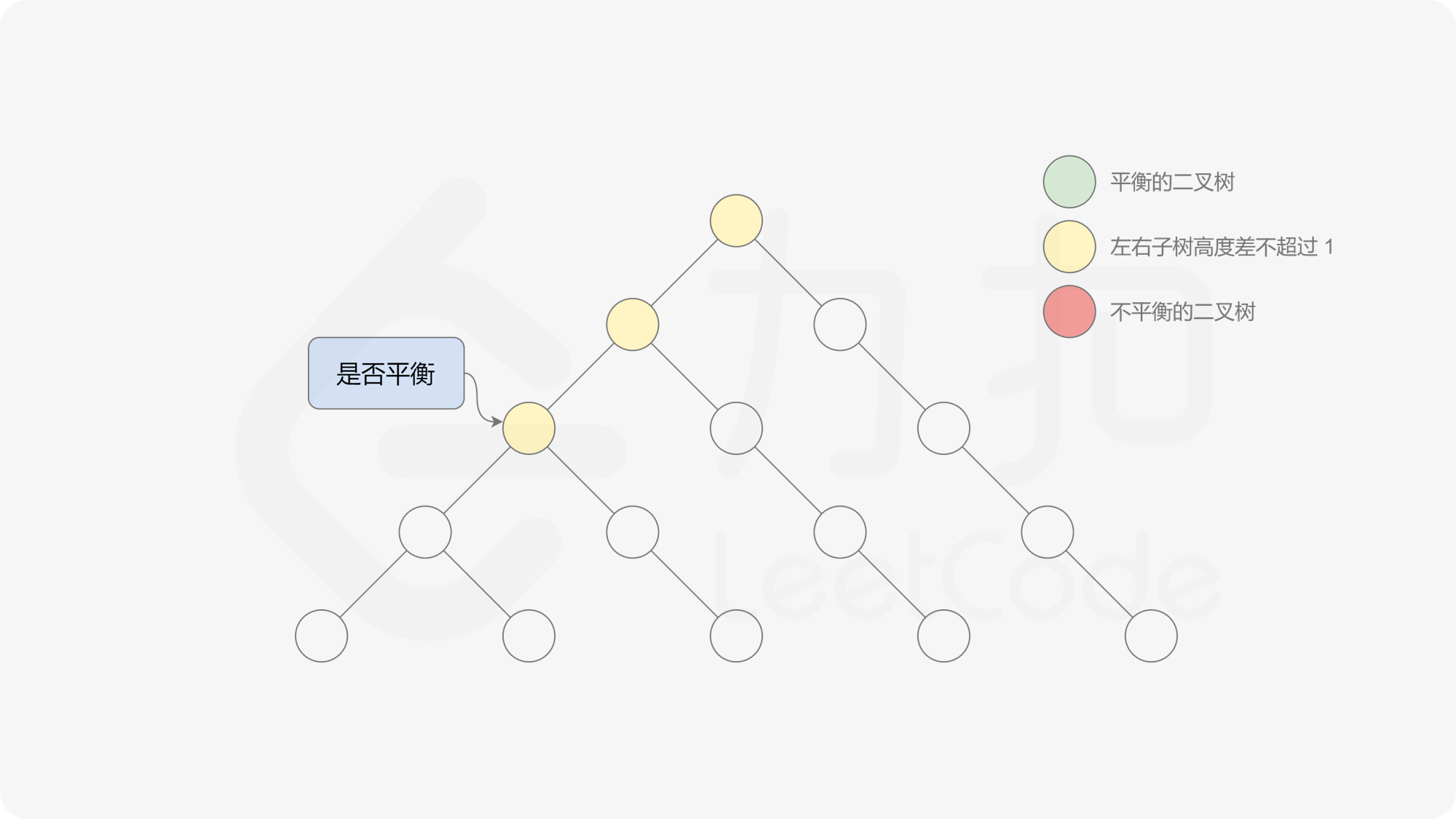
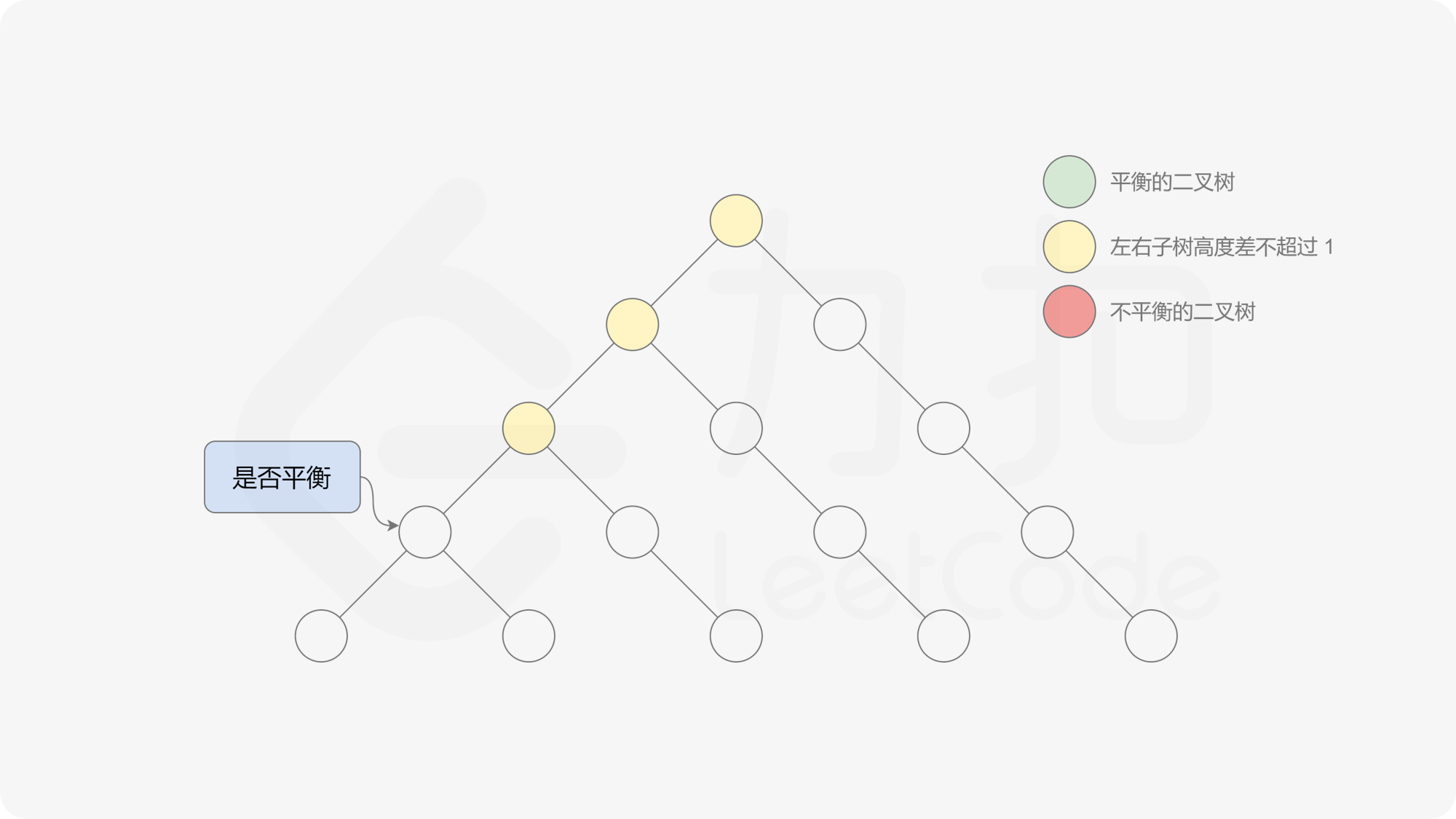
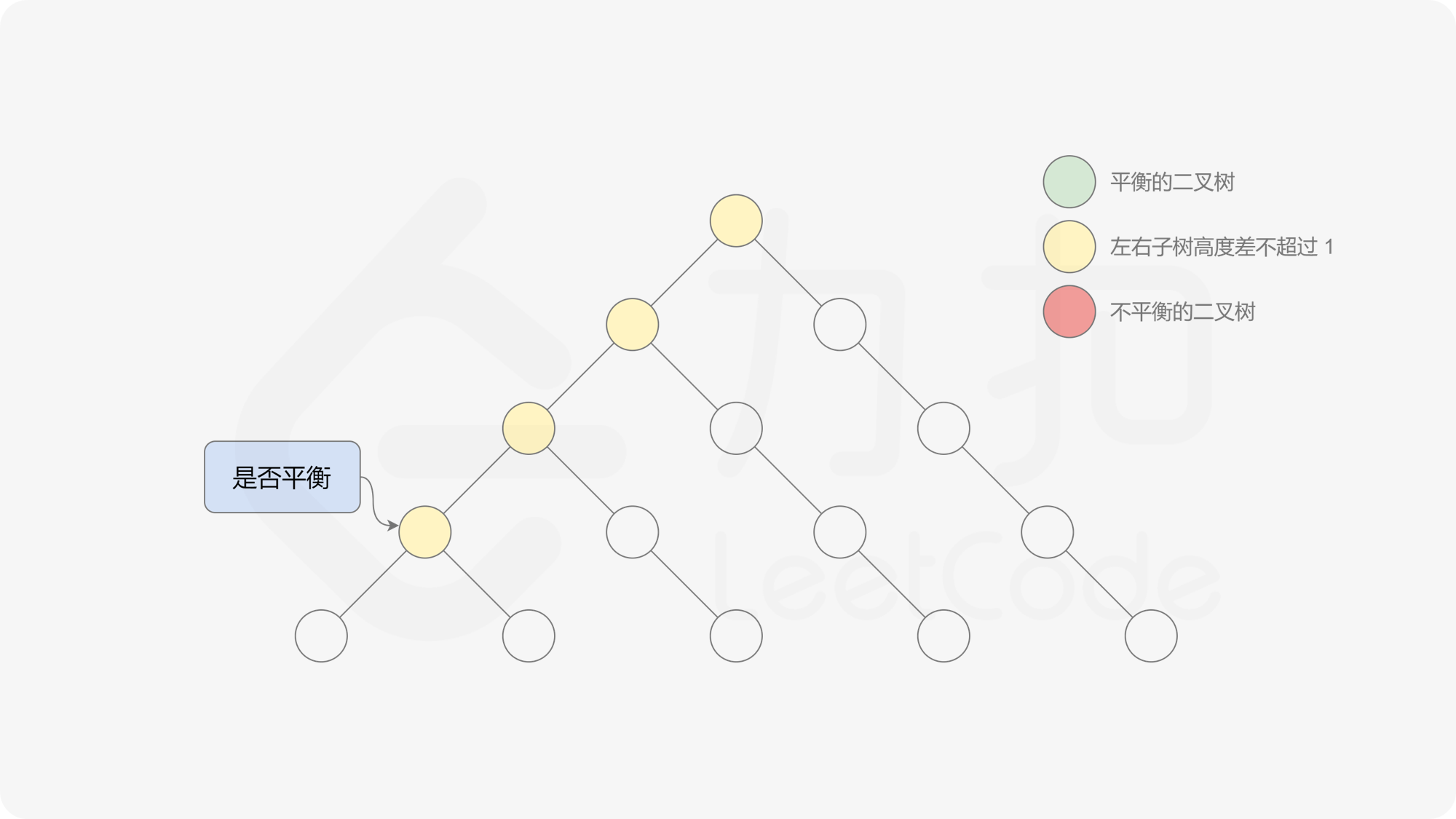
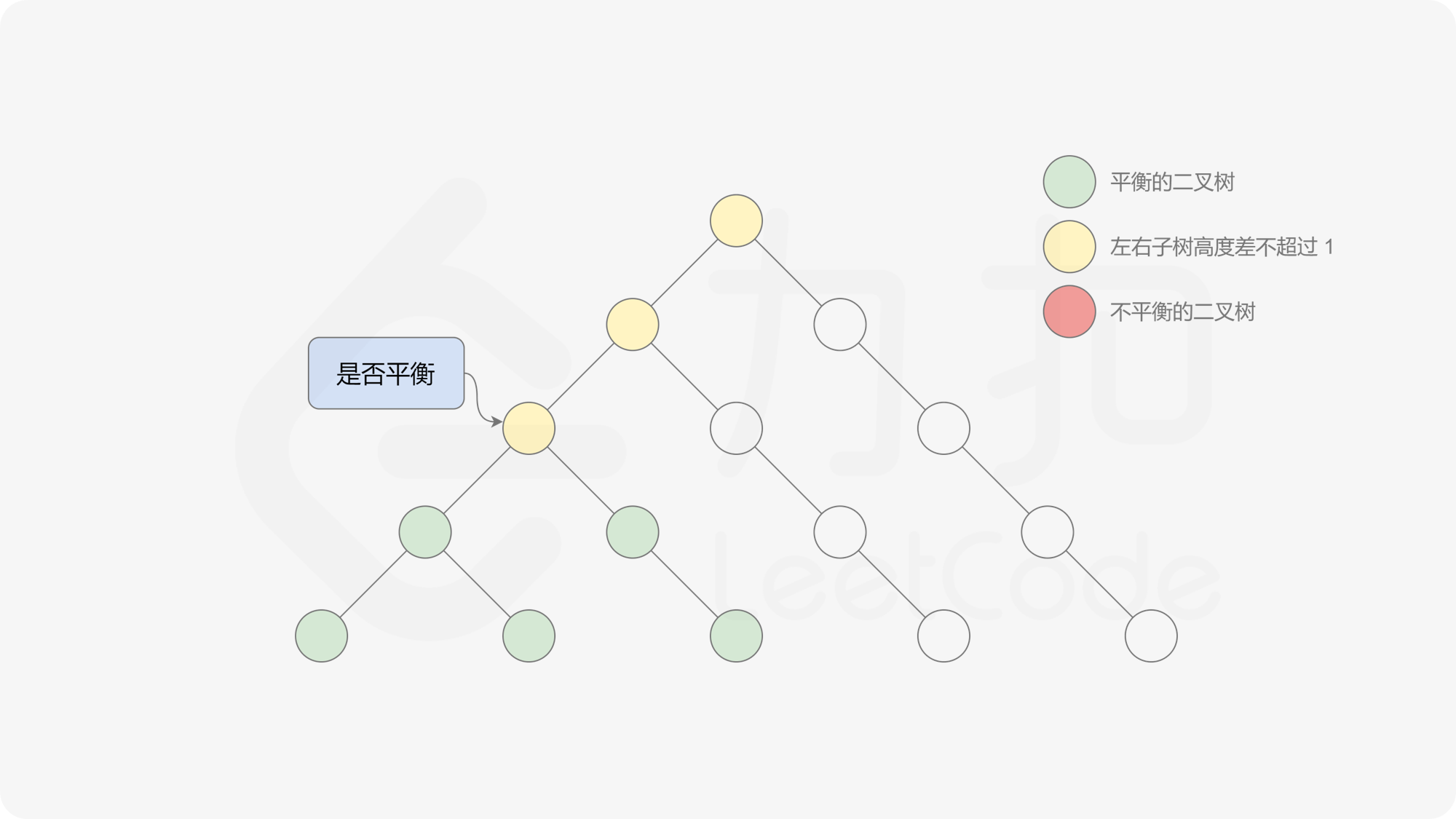
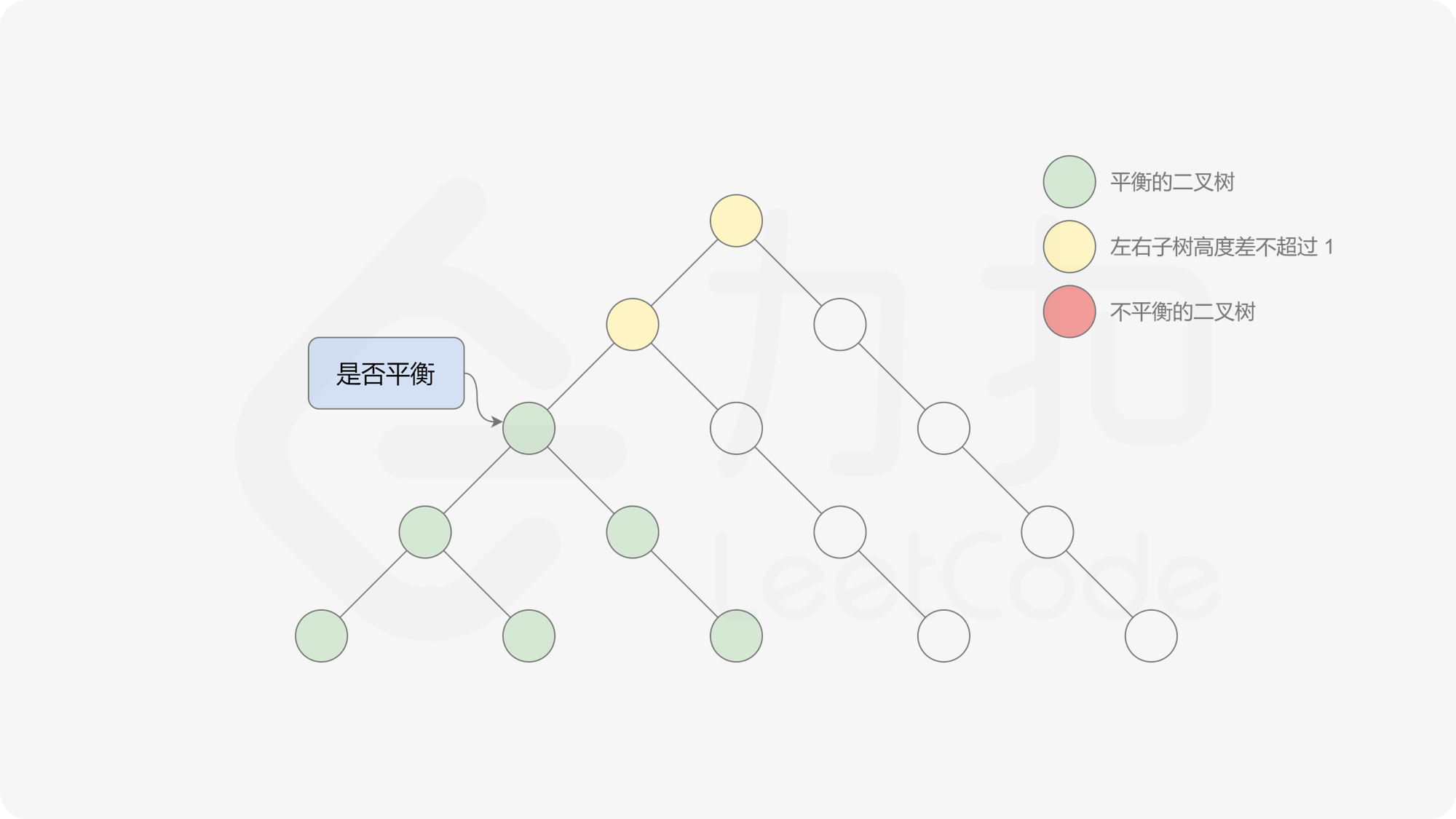
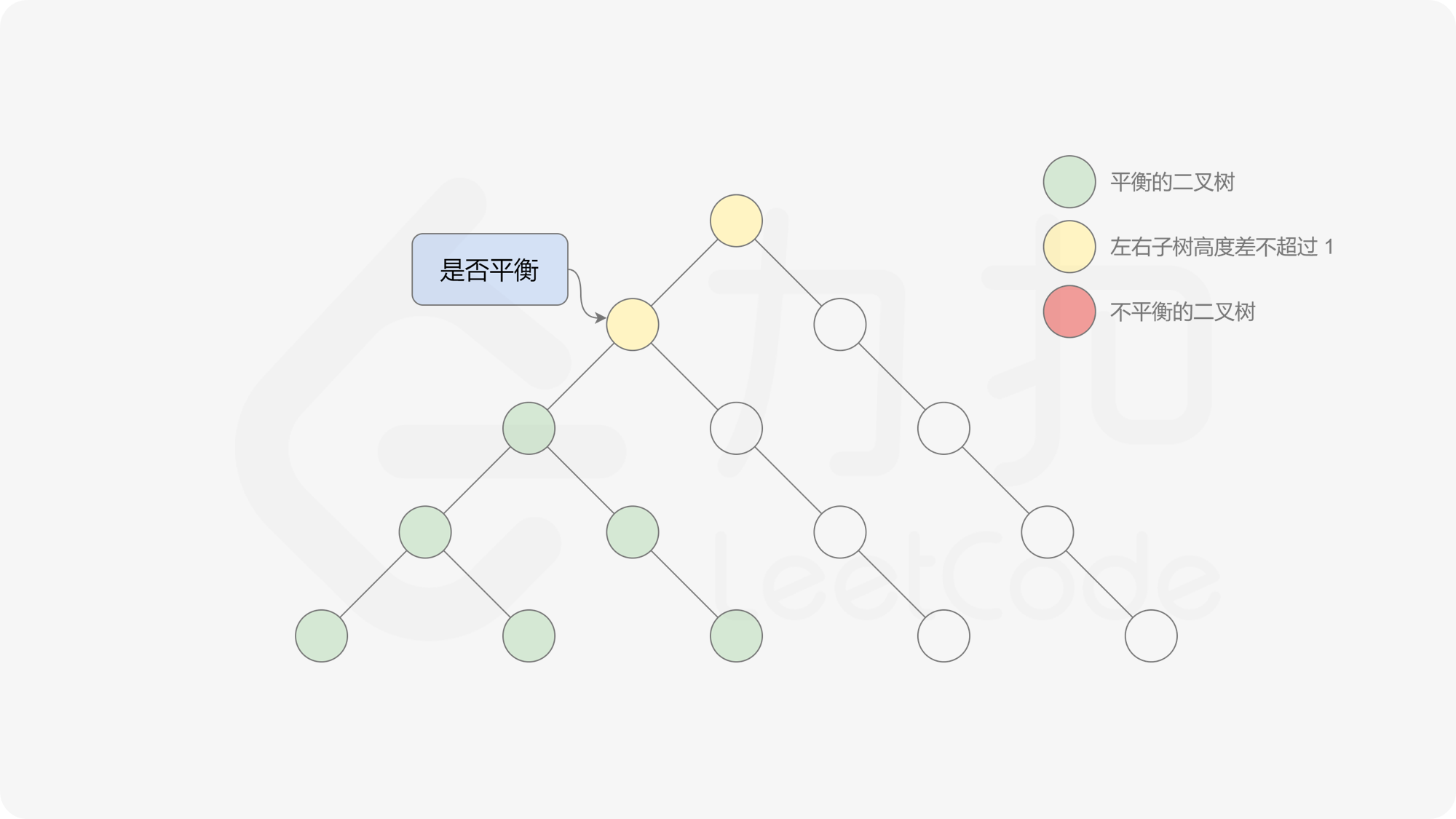
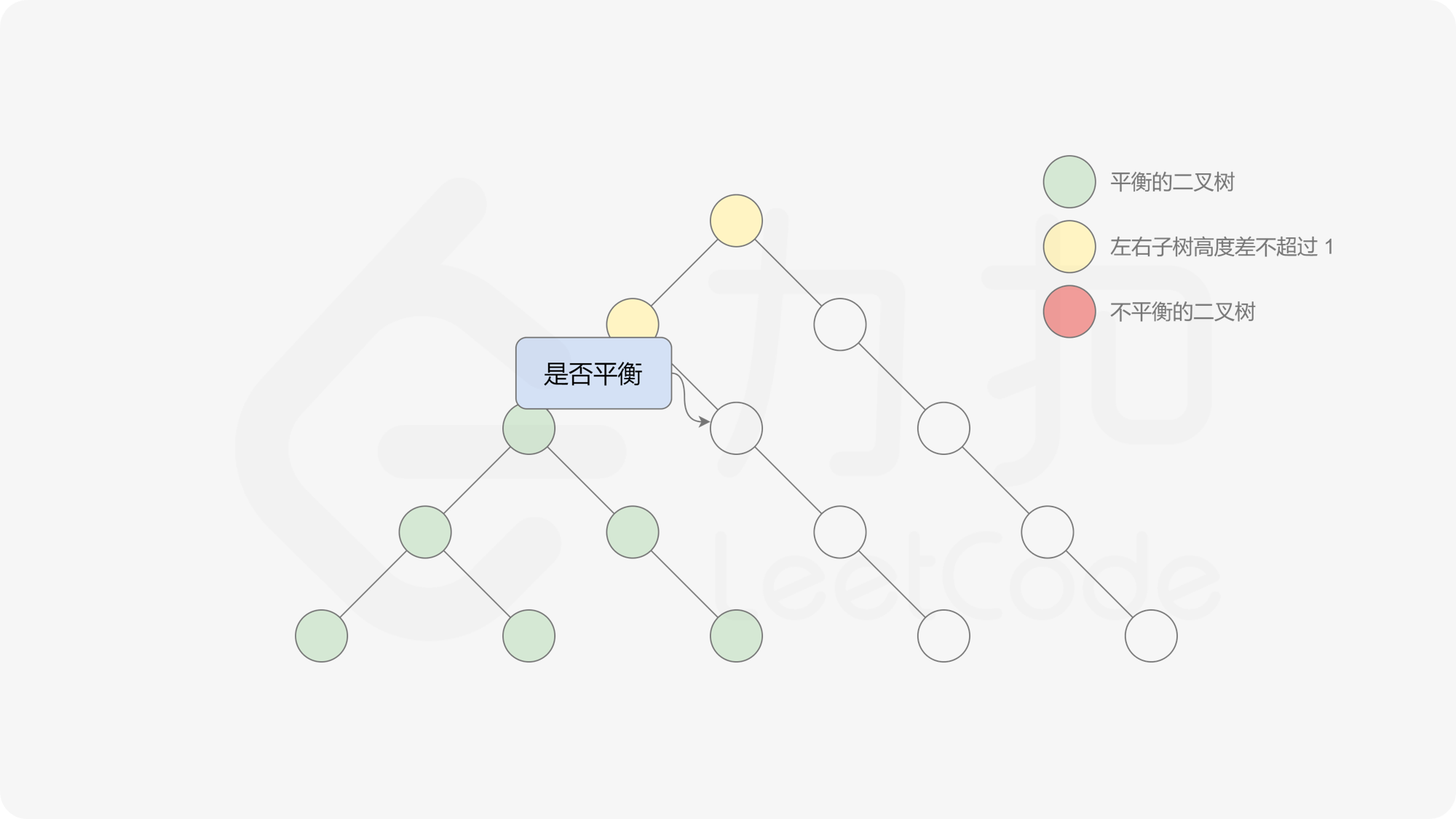
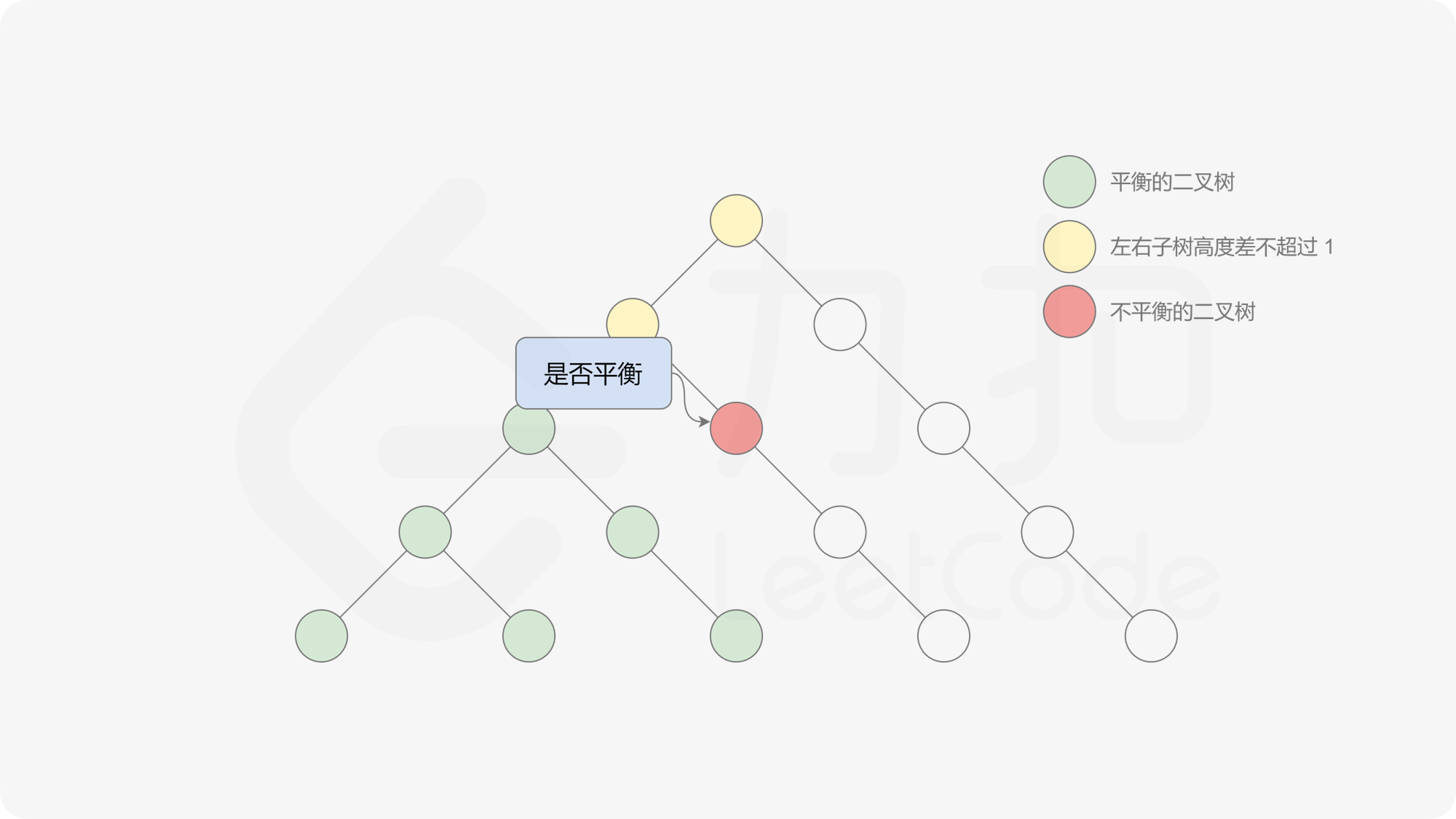
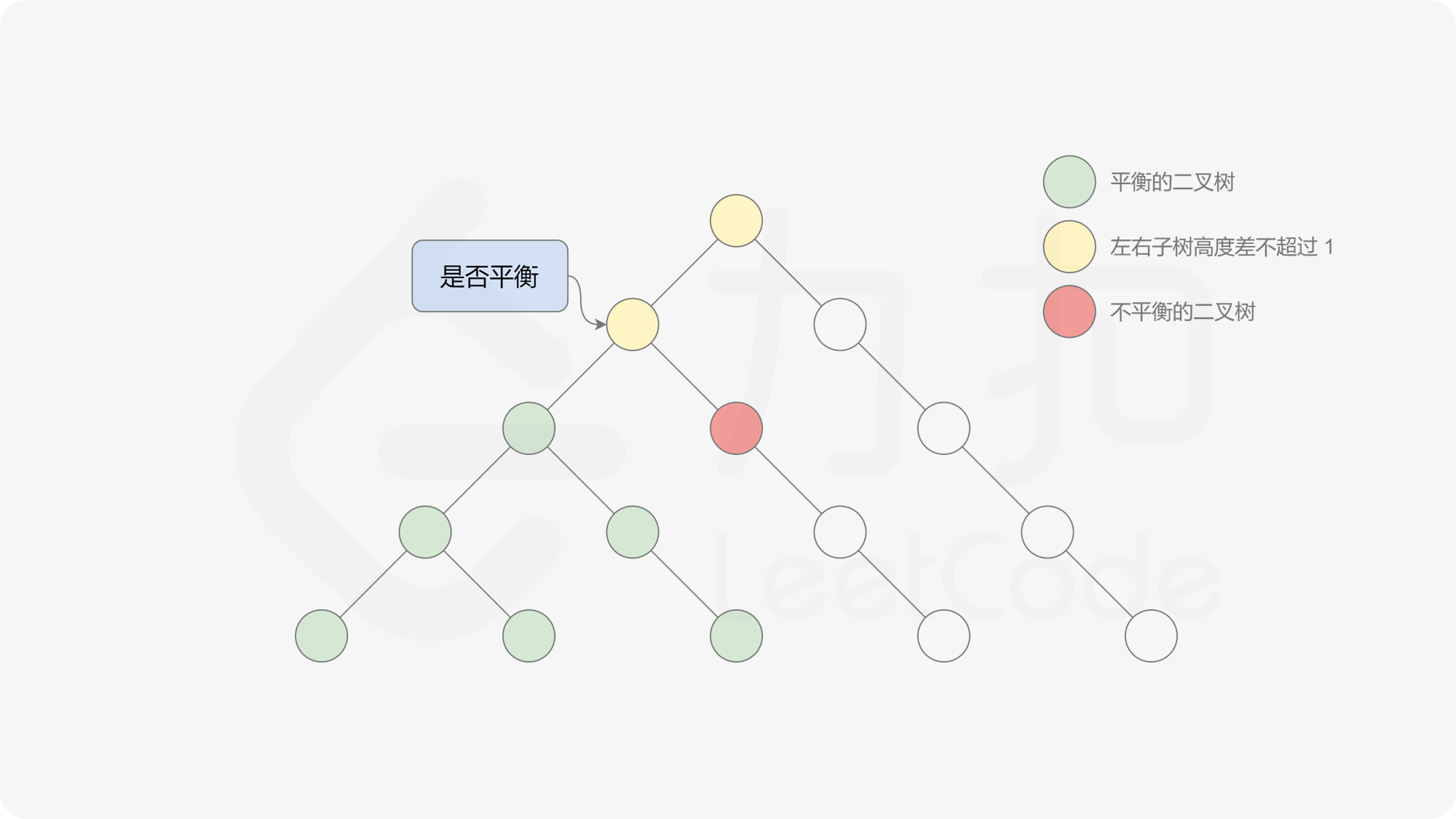
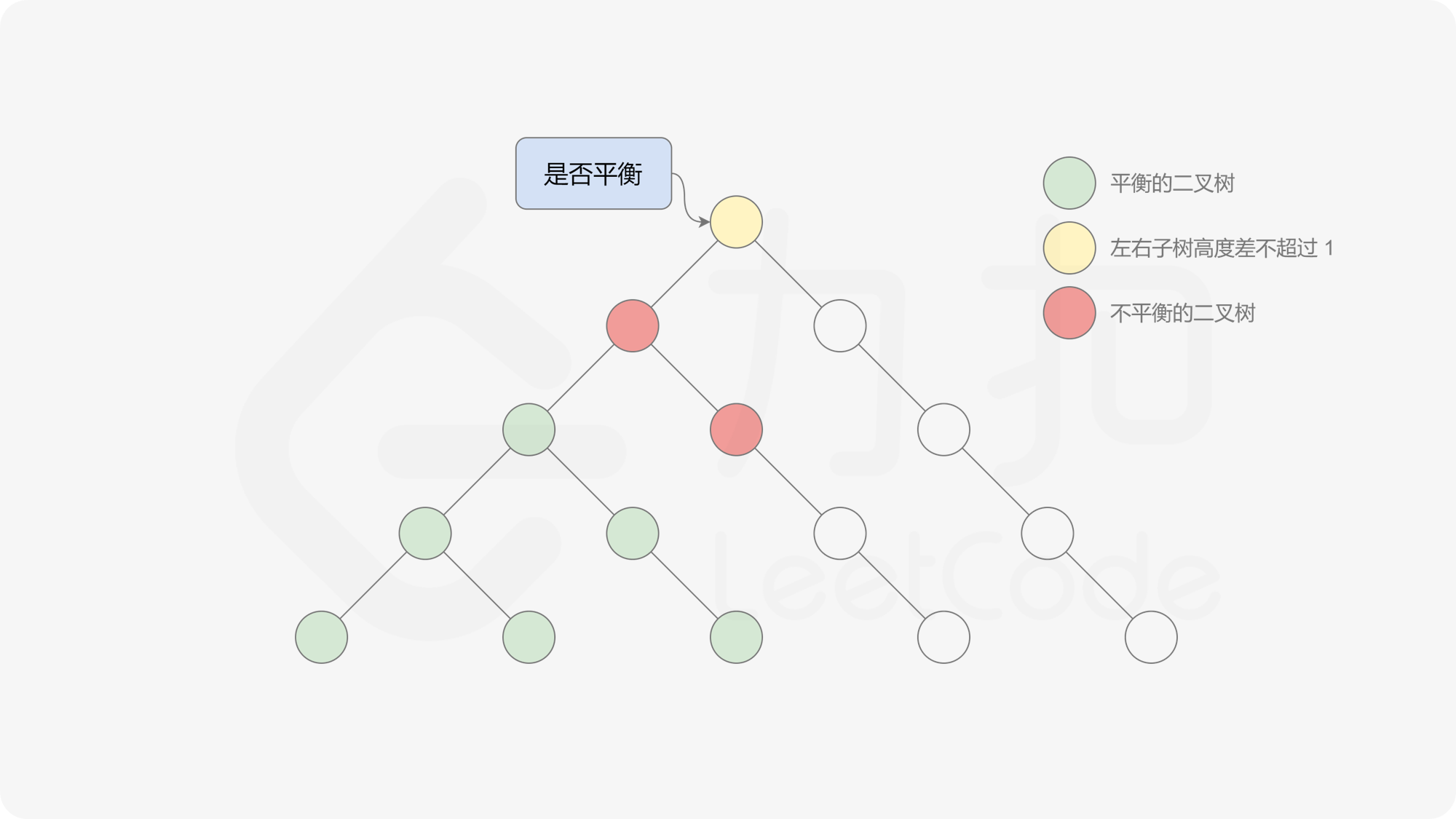
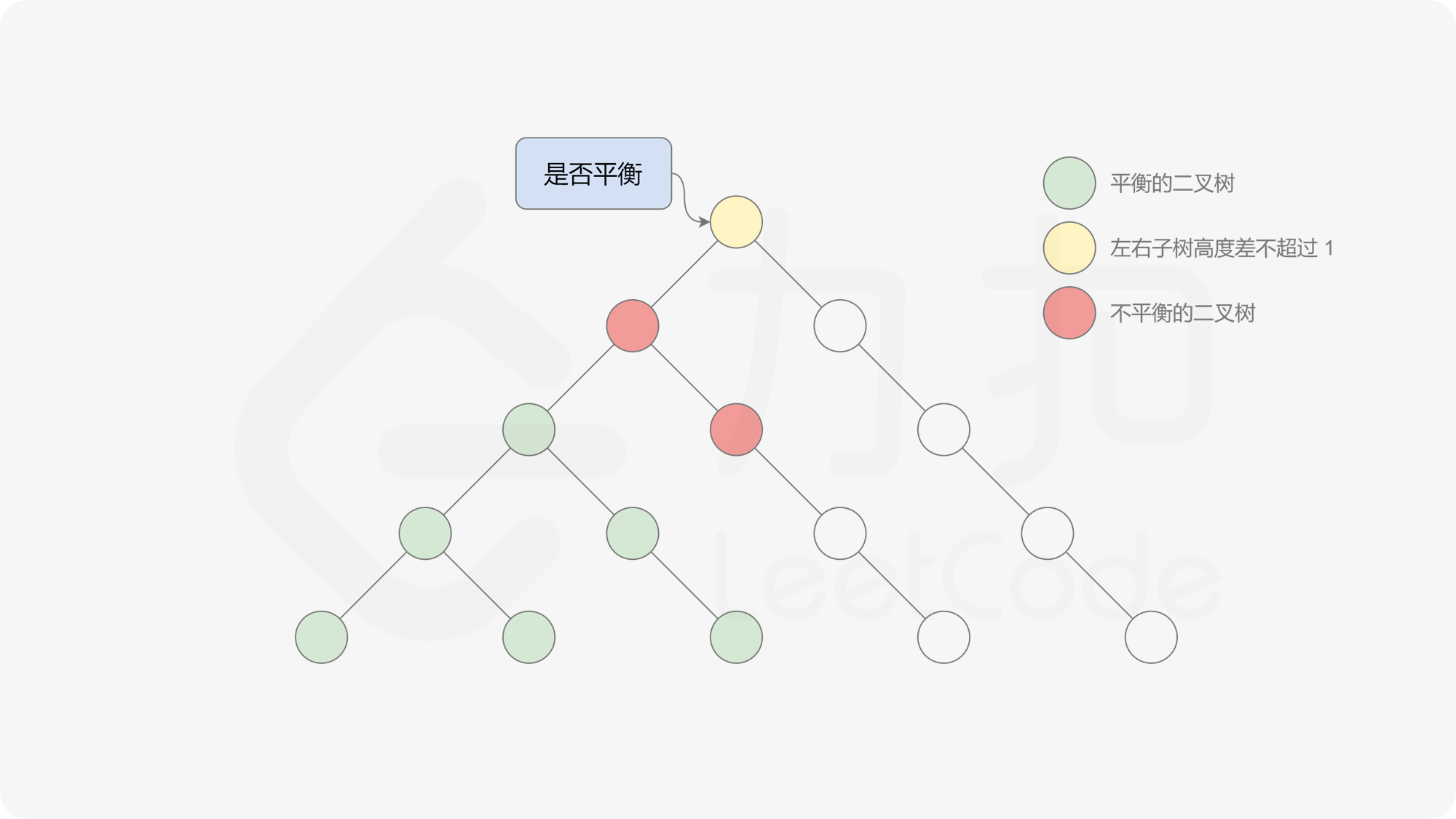
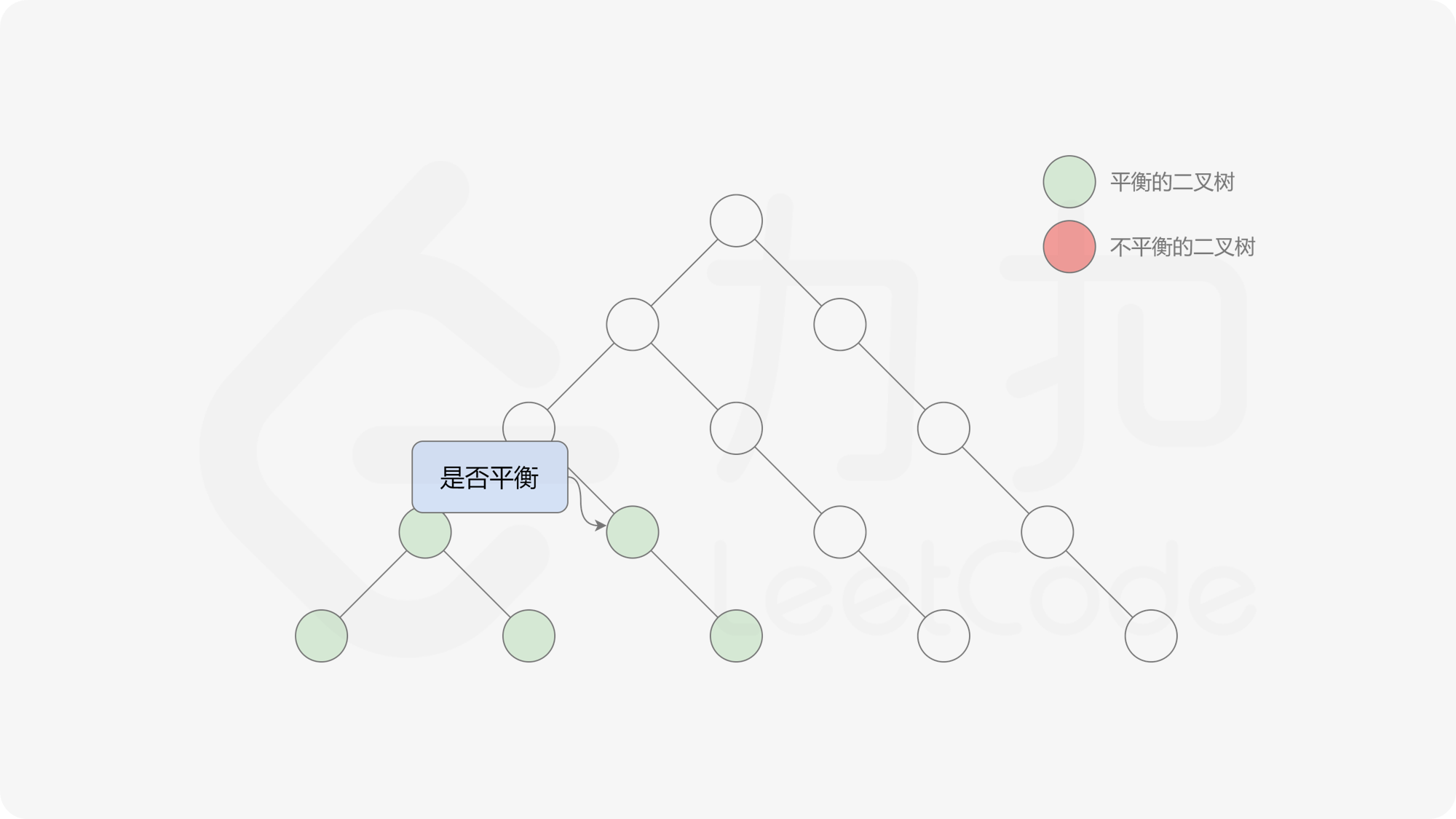
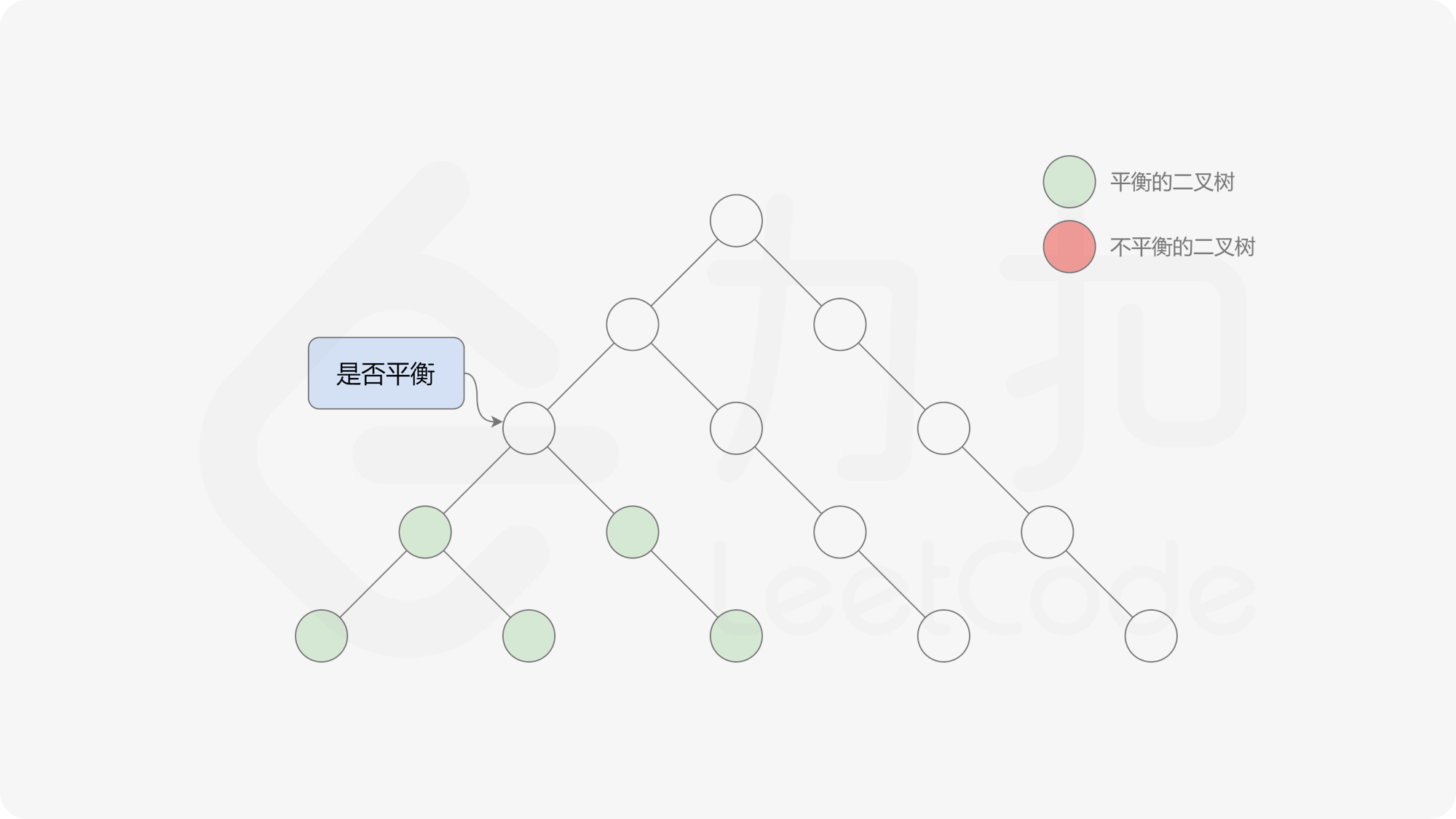
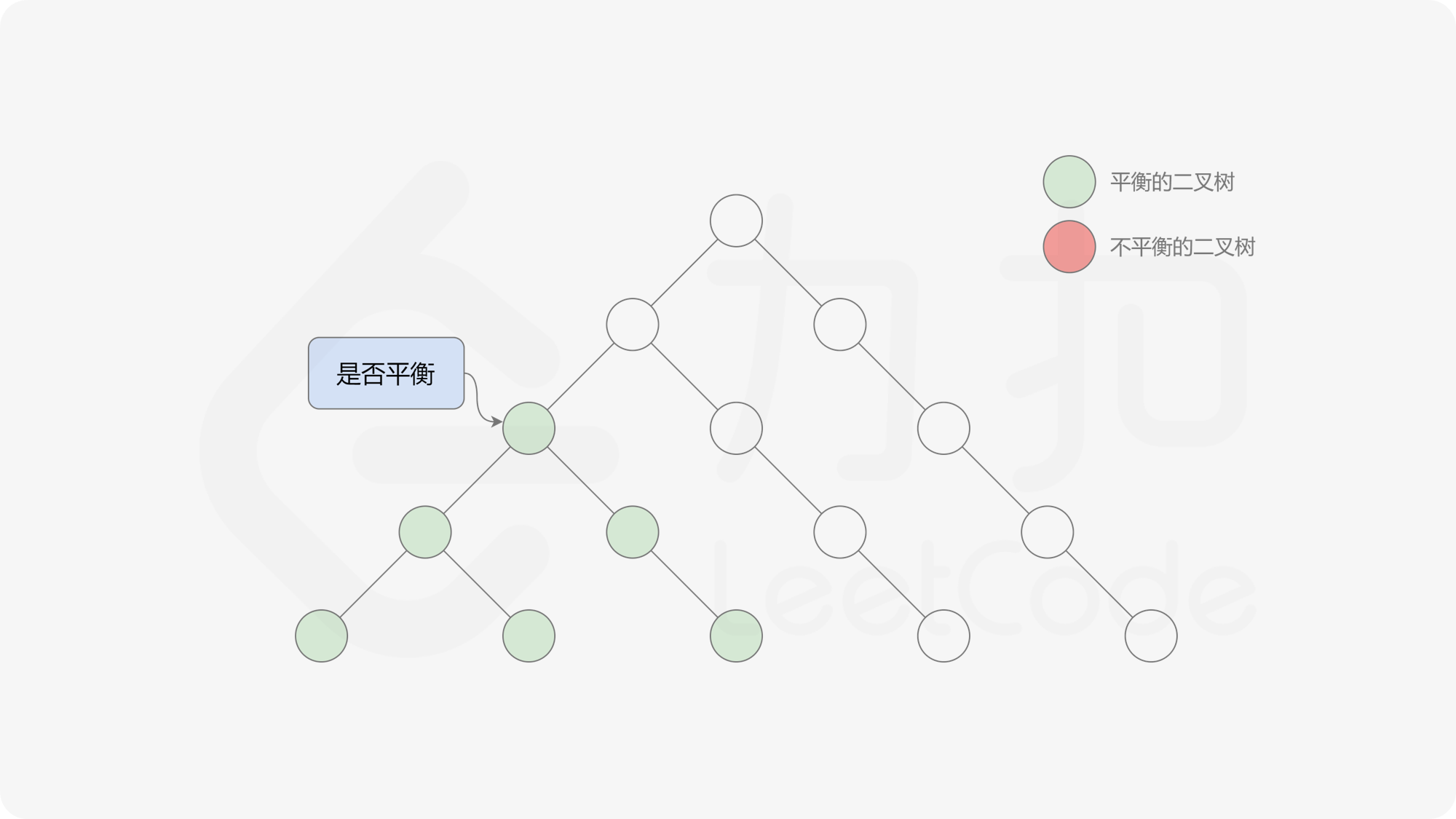
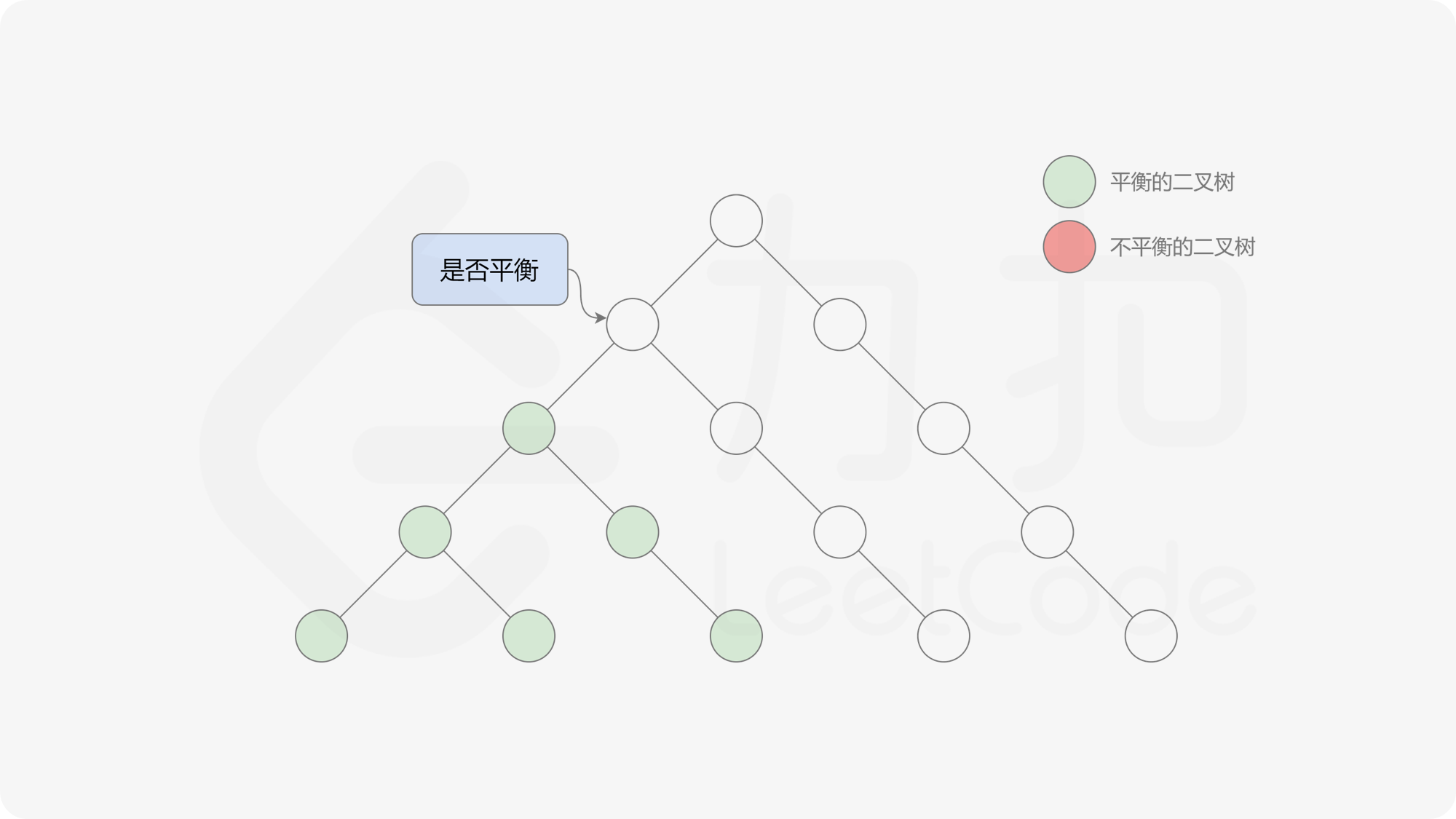
由于该差分数组的变化量绝对值不超过 $1$,因此前缀和满足离散条件下的介值定理,可以使用线段树寻找最右边的 $0$,具体计算方式如下:
- 同时维护区间最大值和最小值。
- 判断 $0$ 是否存在于右区间(位于最大值最小值构成的区间内),若存在则只搜索右区间。
- 否则,搜索左区间。
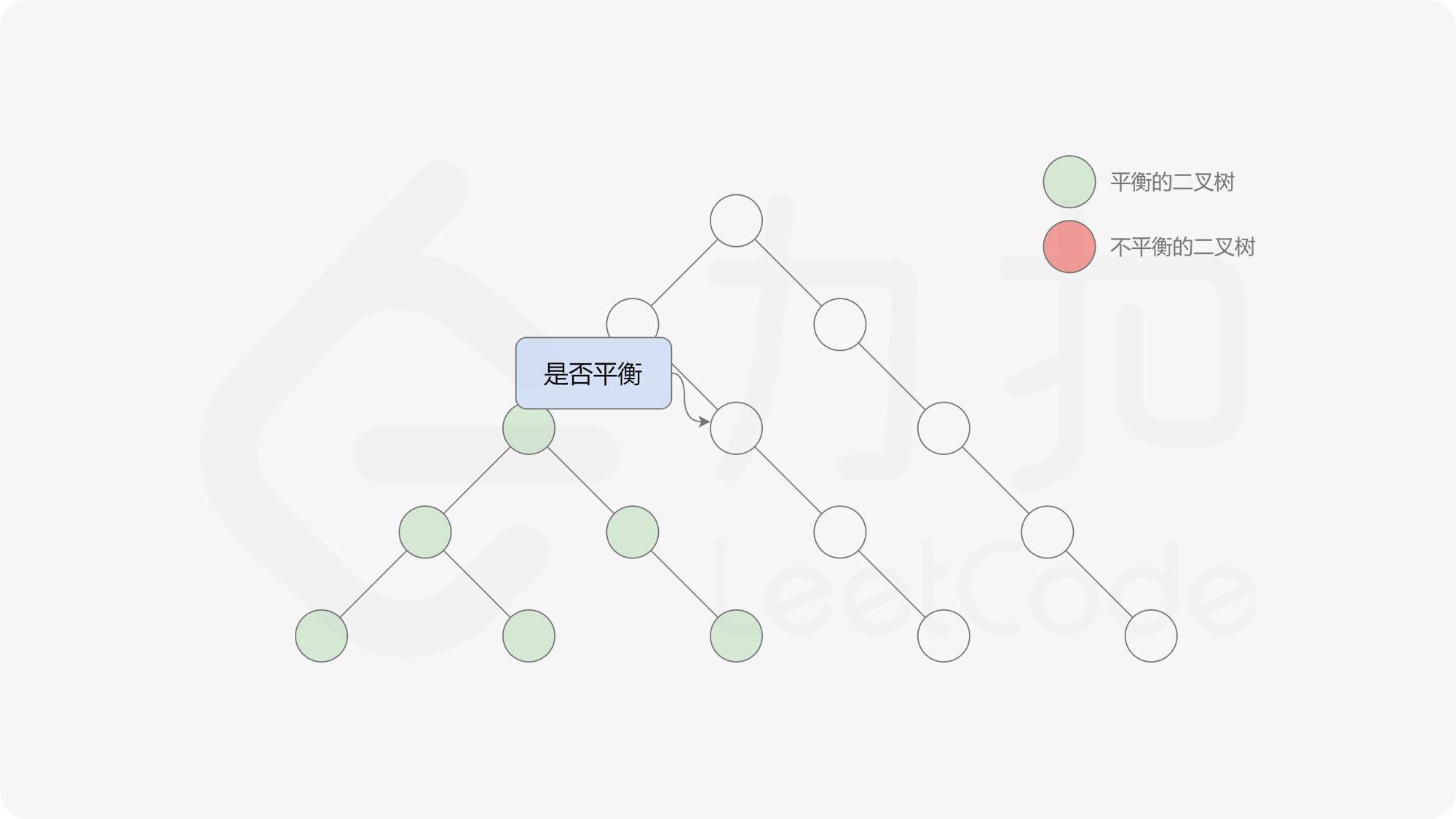
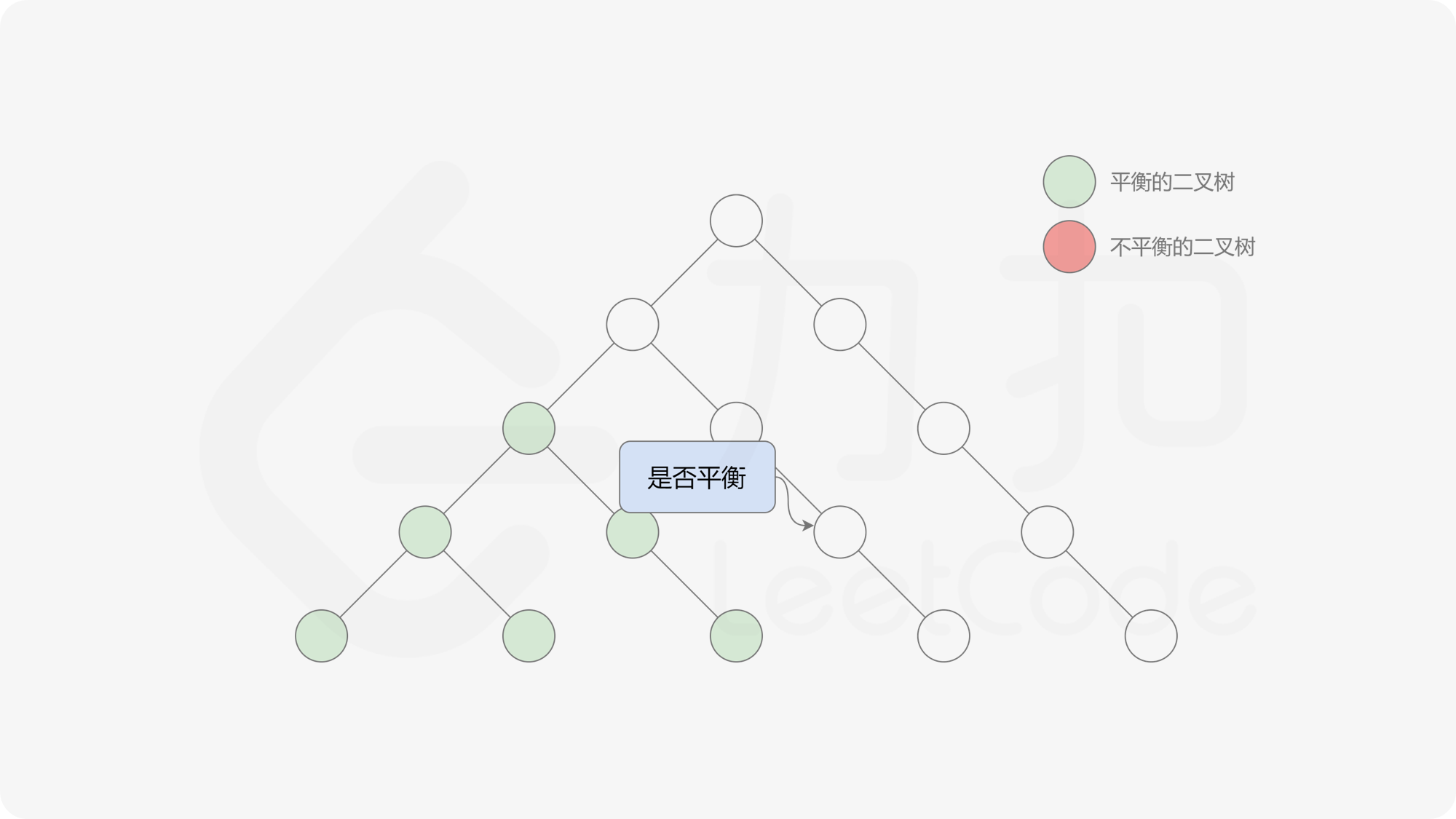
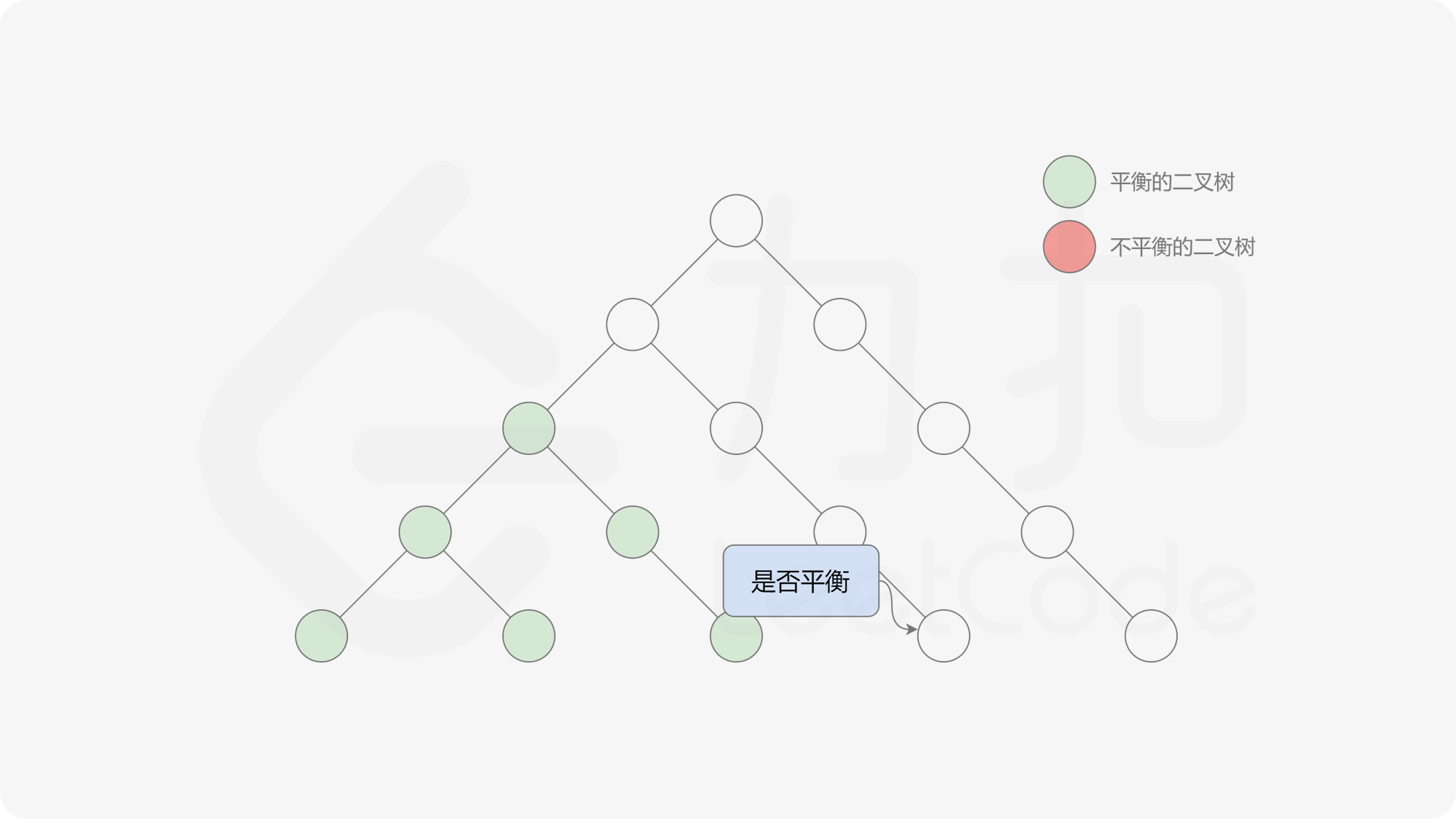
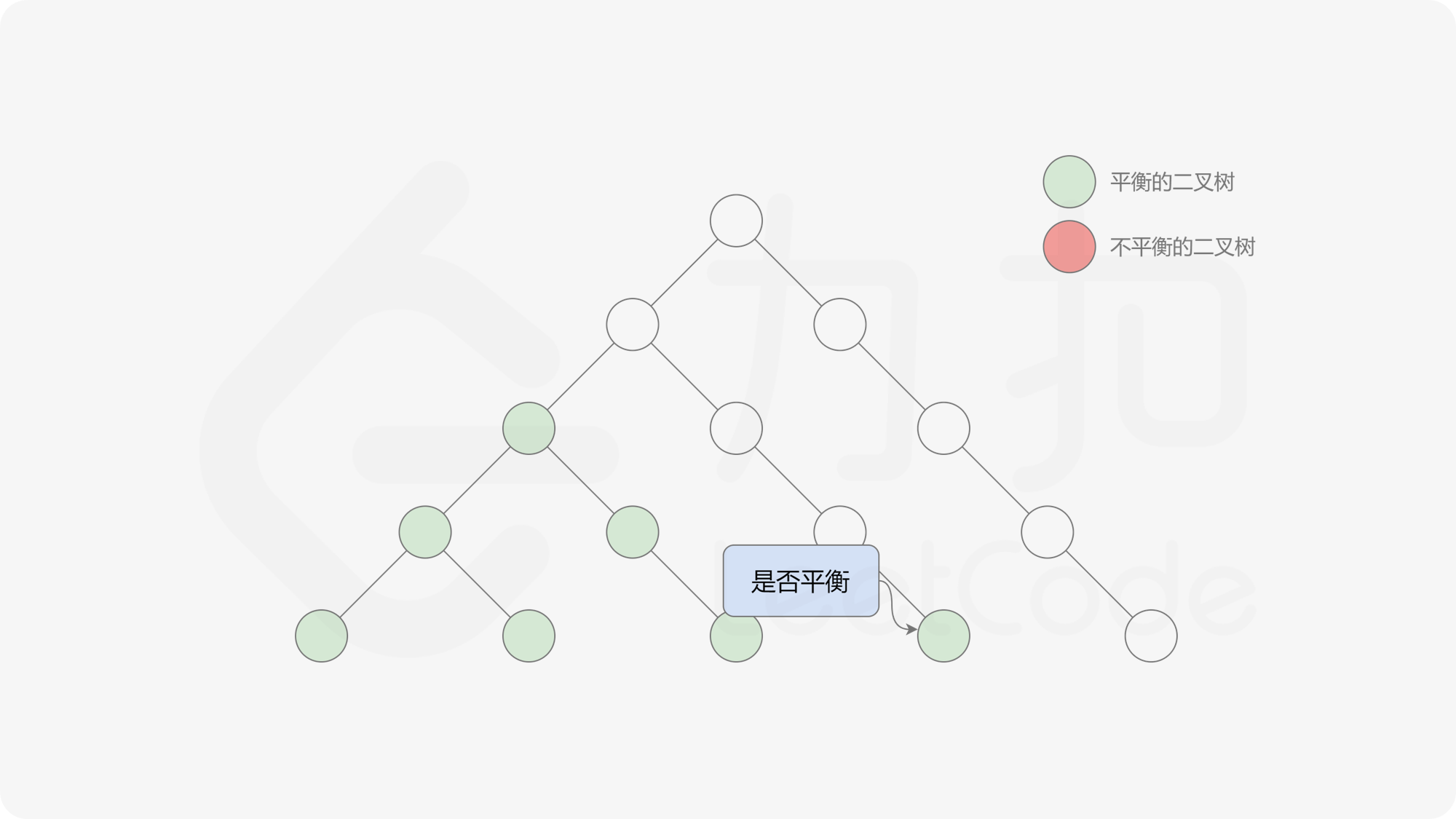
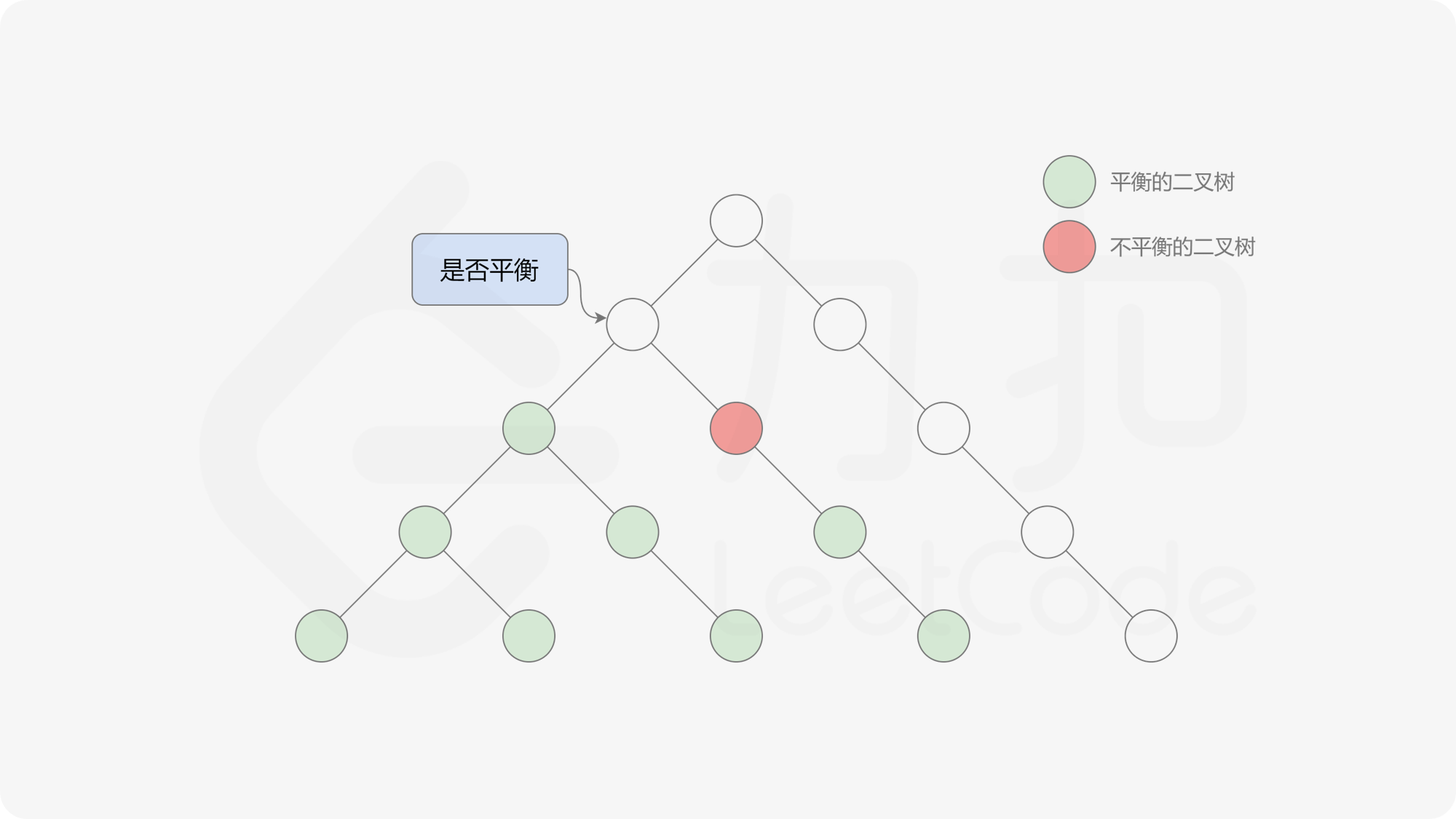
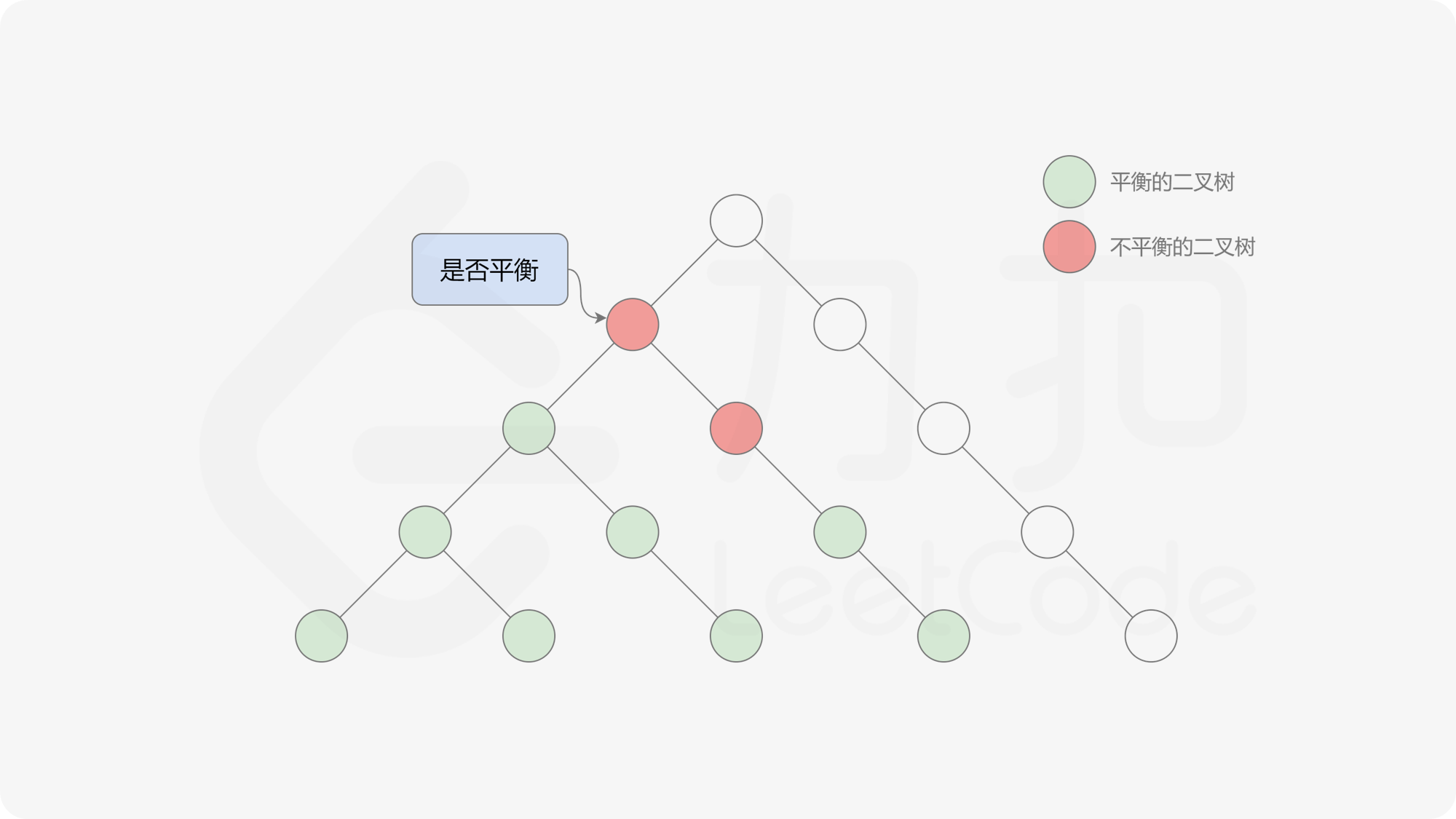
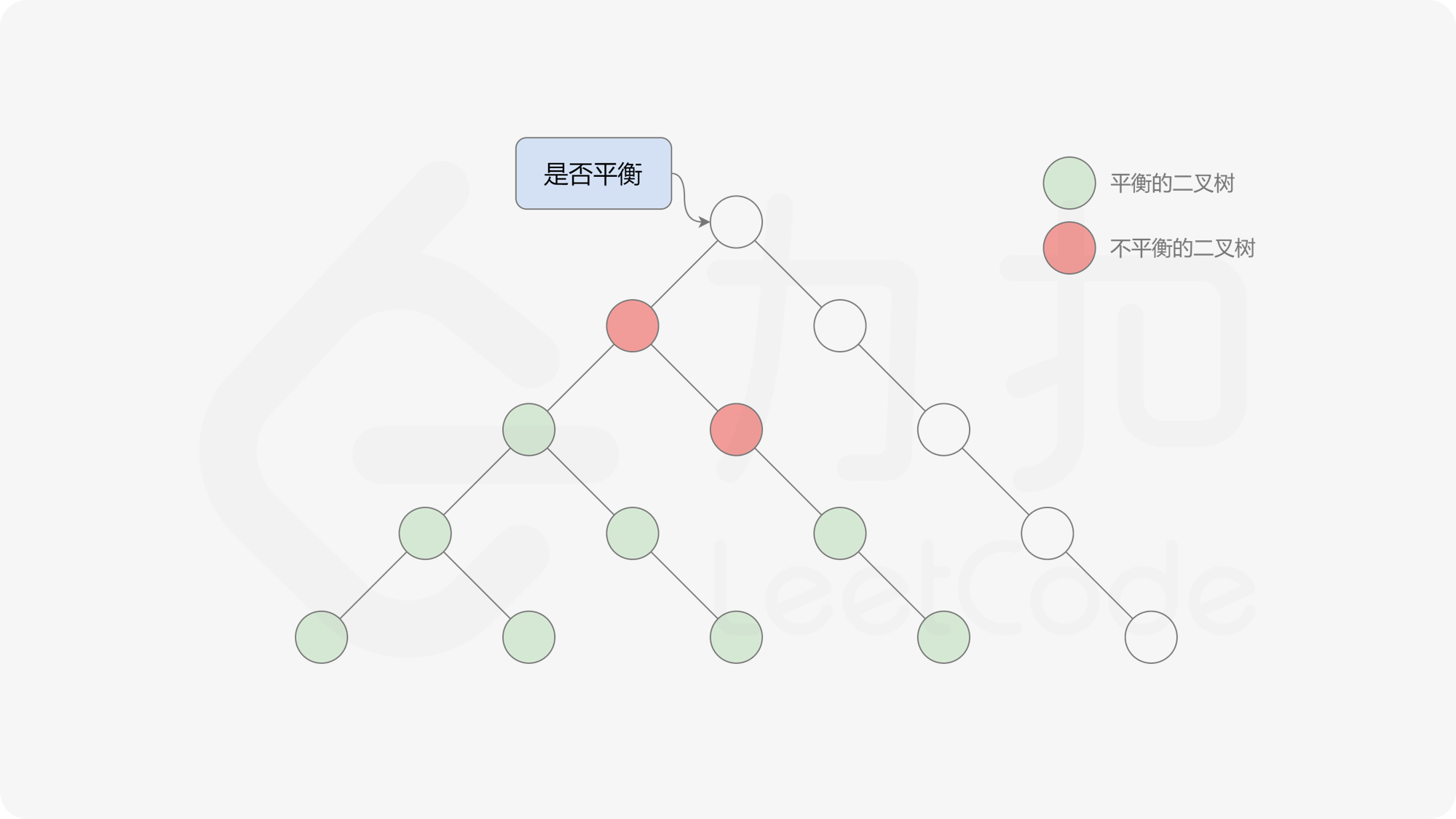
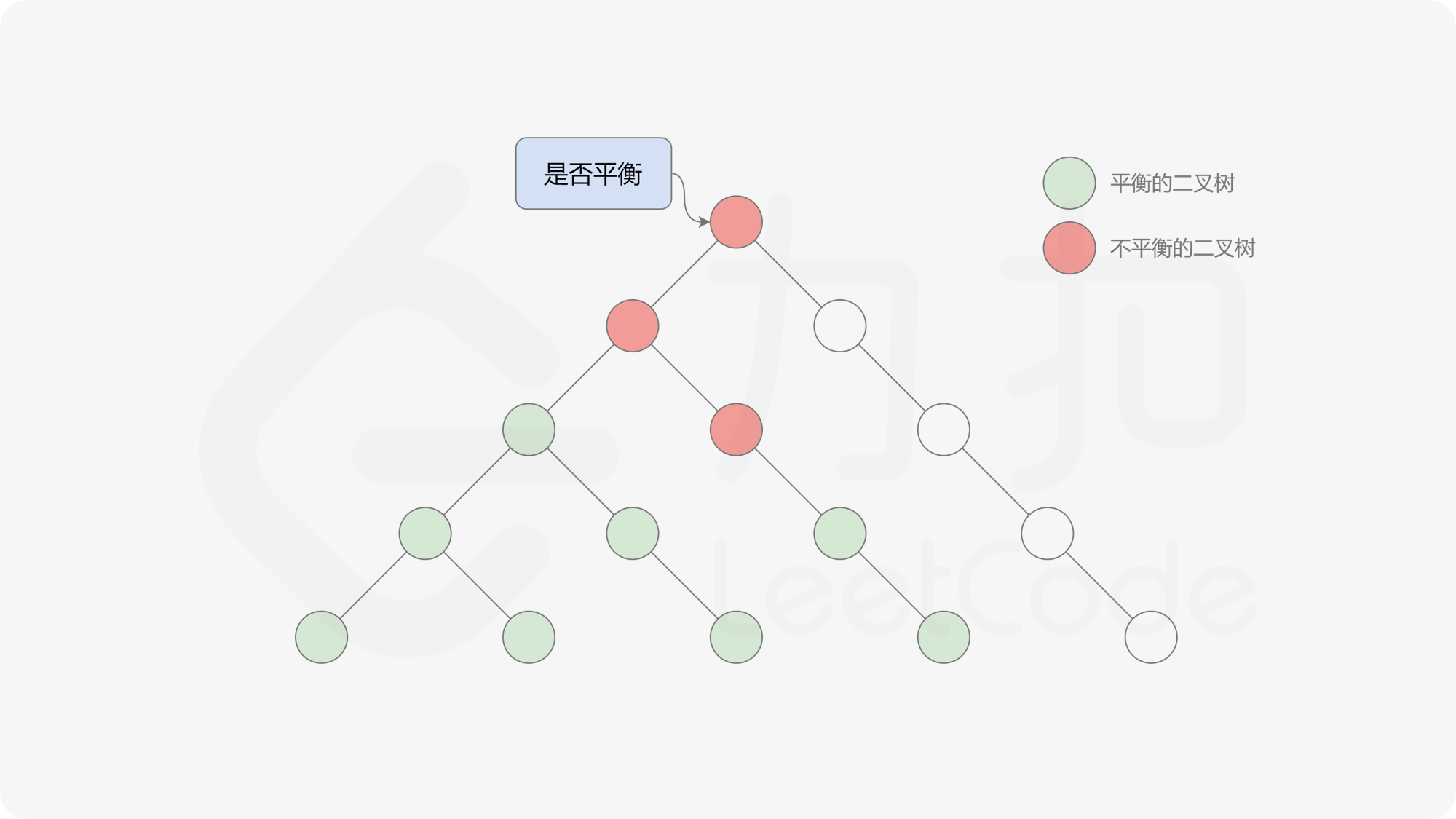
由于满足离散条件下的介值定理,故可以直接通过最大值和最小值判断目标值 $0$ 是否在待搜索区间内,因此也能在 $O(\log n)$ 的时间内搜索完毕。
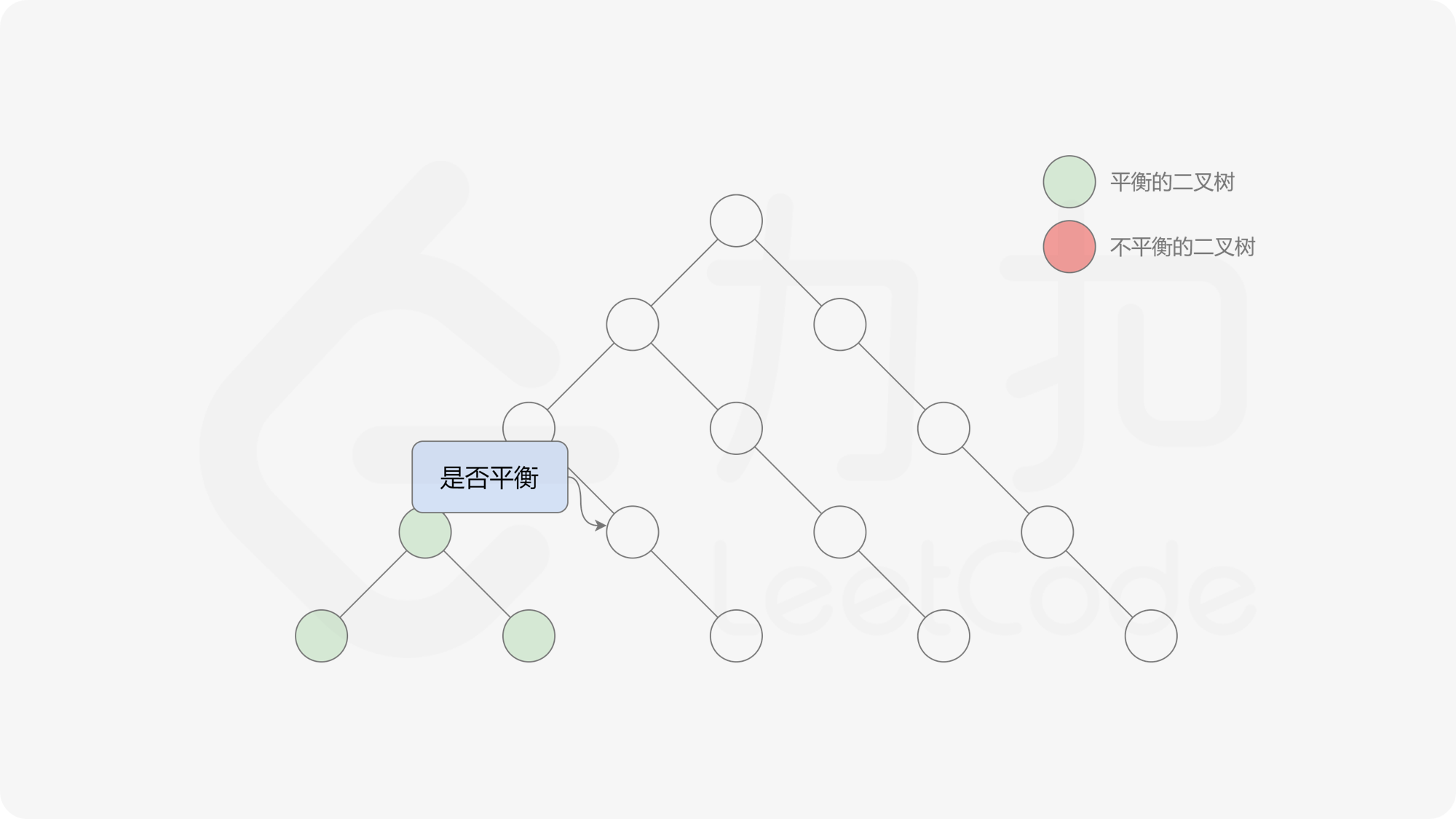
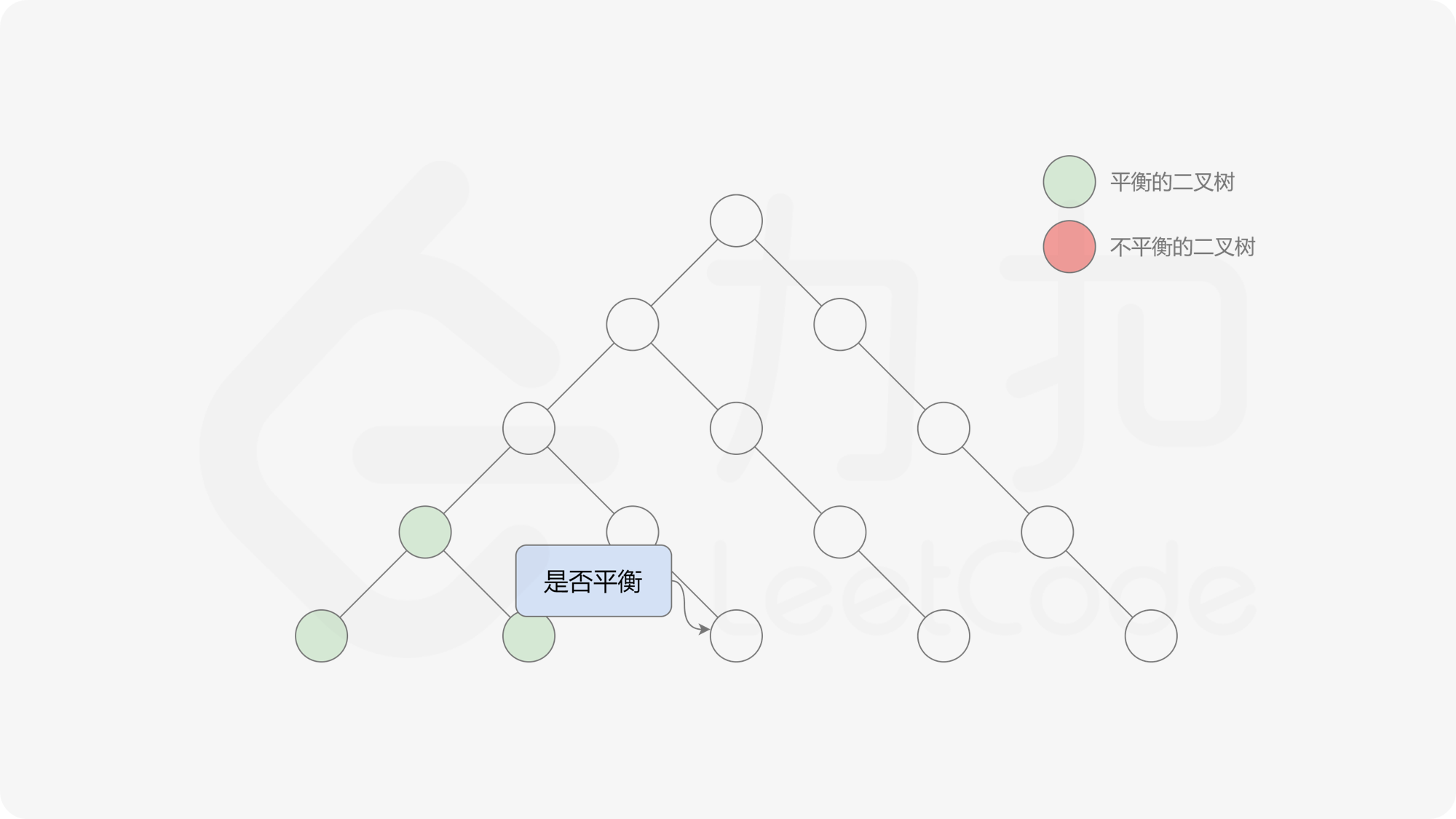
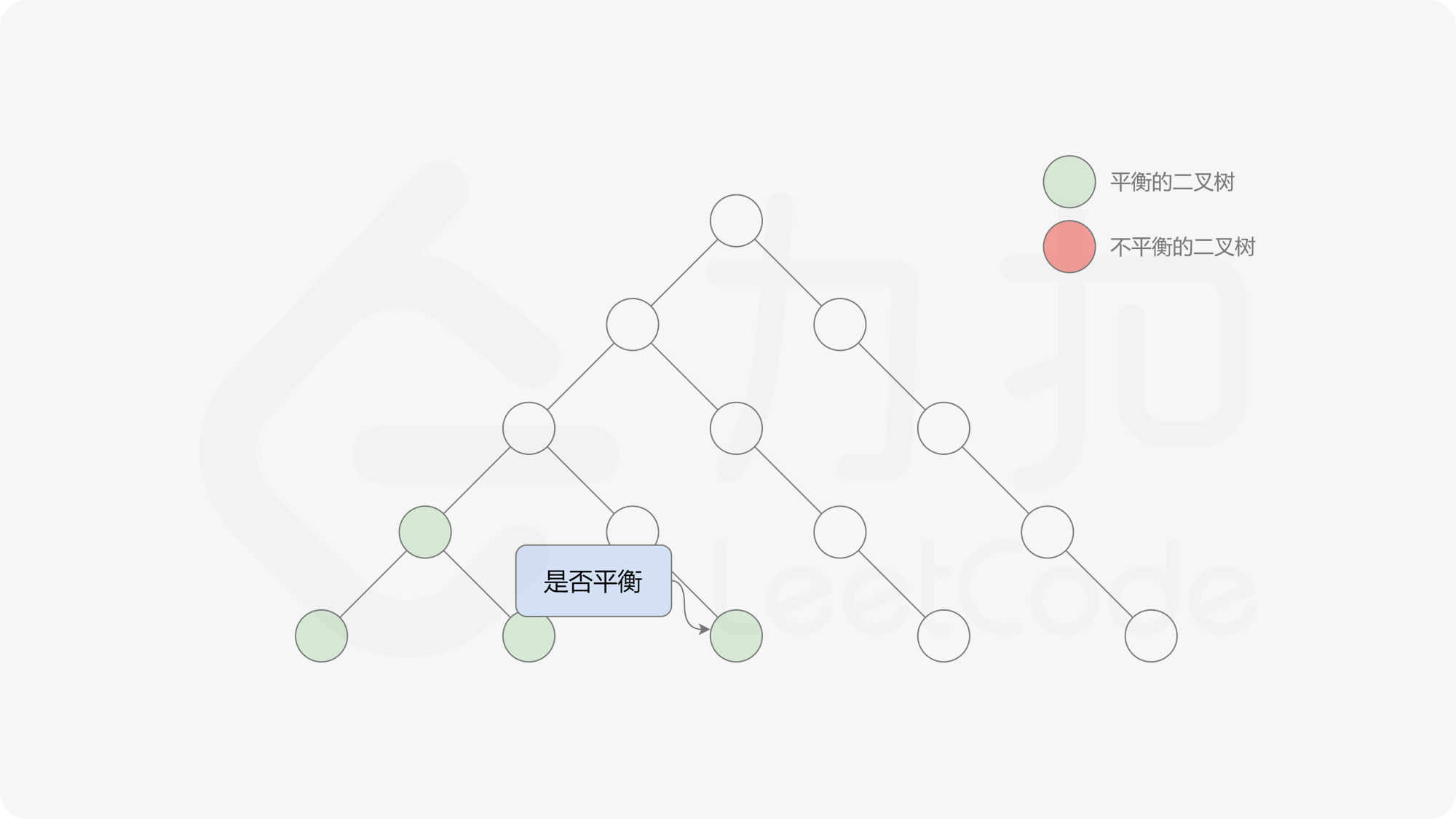
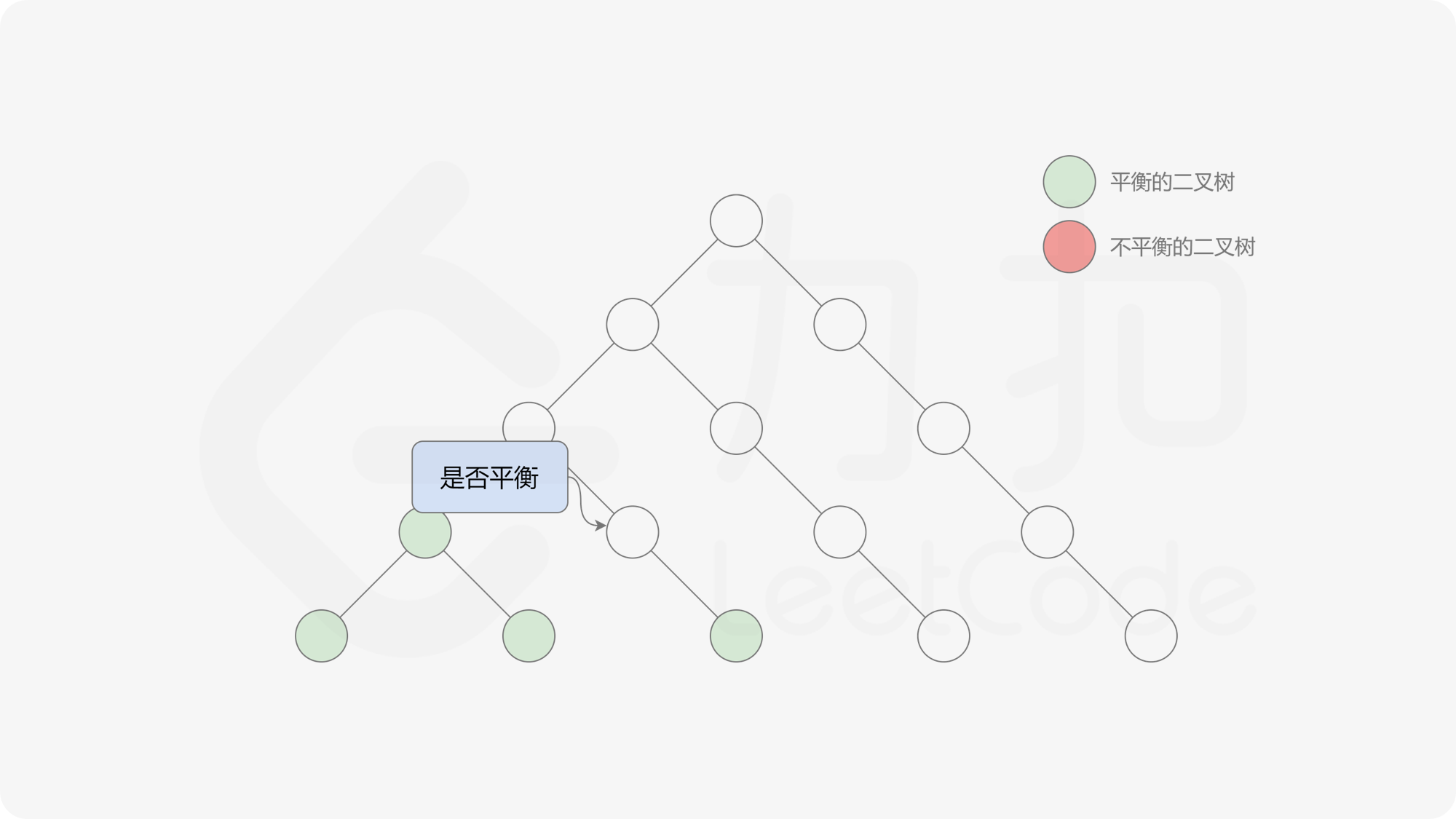
接下来的思路就是遍历左端点,寻找前缀和对应的最右侧的 $0$ 所在位置,得到最长平衡子数组的长度。设当前左边界下标是 $i$,当前最长平衡子数组长度是 $l$,有一个小优化是搜索的起点可以从 $i + l$ 开始,因为更近的结果即便找到也不能更新答案。
最后一个问题是向右移动左端点的过程中,如何撤销前一个位置的元素对前缀和的贡献。
先让我们从差分与前缀和的定义开始理解:差分数组中某位置 $i$ 的非零值 $v_i$,会累加到该位置及其之后的所有前缀和中。例如,若位置 $1$ 的差分贡献为 $-1$,则它会让 $S_1, S_2, \dots, S_N$ 的值都减小 $1$;再比如,若元素 $x$ 先后出现在位置 $p_1$ 和 $p_2$,我们可以认为位置 $p_1$ 处的 $x$ 负责区间 $[p_1, p_2 - 1]$ 上的贡献,而位置 $p_2$ 处的 $x$ 则负责 $[p_2, \dots]$ 上的贡献。
$$
[ \dots, 0, \underbrace{1, 1, \dots, 1}{\text{由第 1 个 x 贡献}}, \underbrace{1, 1, \dots, 1}{\text{由第 2 个 x 贡献}}, \dots ]
$$
因此,我们可以将每种元素出现的所有位置记录到各自的队列中,在更新左边界时,得到要撤销贡献的元素在前缀和中的贡献区间,然后在该区间上减去它的贡献即可。显然,这样区间加法操作也可以使用线段树完成。
基于以上算法,我们先统计前缀和以及元素出现的次数,然后不断更新左端点,使用线段树维护前缀和,寻找最右侧的 $0$,并更新全局最优解即可。
代码
###C++
struct LazyTag {
int to_add = 0;
LazyTag& operator+=(const LazyTag& other) {
this->to_add += other.to_add;
return *this;
}
bool has_tag() const { return to_add != 0; }
void clear() { to_add = 0; }
};
struct SegmentTreeNode {
int min_value = 0;
int max_value = 0;
// int data = 0; // 只有叶子节点使用, 本题不需要
LazyTag lazy_tag;
};
class SegmentTree {
public:
int n;
vector<SegmentTreeNode> tree;
SegmentTree(const vector<int>& data) : n(data.size()) {
tree.resize(n * 4 + 1);
build(data, 1, n, 1);
}
void add(int l, int r, int val) {
LazyTag tag{val};
update(l, r, tag, 1, n, 1);
}
int find_last(int start, int val) {
if (start > n) {
return -1;
}
return find(start, n, val, 1, n, 1);
}
private:
inline void apply_tag(int i, const LazyTag& tag) {
tree[i].min_value += tag.to_add;
tree[i].max_value += tag.to_add;
tree[i].lazy_tag += tag;
}
inline void pushdown(int i) {
if (tree[i].lazy_tag.has_tag()) {
LazyTag tag = tree[i].lazy_tag;
apply_tag(i << 1, tag);
apply_tag(i << 1 | 1, tag);
tree[i].lazy_tag.clear();
}
}
inline void pushup(int i) {
tree[i].min_value =
std::min(tree[i << 1].min_value, tree[i << 1 | 1].min_value);
tree[i].max_value =
std::max(tree[i << 1].max_value, tree[i << 1 | 1].max_value);
}
void build(const vector<int>& data, int l, int r, int i) {
if (l == r) {
tree[i].min_value = tree[i].max_value = data[l - 1];
return;
}
int mid = l + ((r - l) >> 1);
build(data, l, mid, i << 1);
build(data, mid + 1, r, i << 1 | 1);
pushup(i);
}
void update(int target_l, int target_r, const LazyTag& tag, int l, int r,
int i) {
if (target_l <= l && r <= target_r) {
apply_tag(i, tag);
return;
}
pushdown(i);
int mid = l + ((r - l) >> 1);
if (target_l <= mid)
update(target_l, target_r, tag, l, mid, i << 1);
if (target_r > mid)
update(target_l, target_r, tag, mid + 1, r, i << 1 | 1);
pushup(i);
}
int find(int target_l, int target_r, int val, int l, int r, int i) {
if (tree[i].min_value > val || tree[i].max_value < val) {
return -1;
}
// 根据介值定理,此时区间内必然存在解
if (l == r) {
return l;
}
pushdown(i);
int mid = l + ((r - l) >> 1);
// target_l 一定小于等于 r(=n)
if (target_r >= mid + 1) {
int res = find(target_l, target_r, val, mid + 1, r, i << 1 | 1);
if (res != -1)
return res;
}
if (l <= target_r && mid >= target_l) {
return find(target_l, target_r, val, l, mid, i << 1);
}
return -1;
}
};
class Solution {
public:
int longestBalanced(vector<int>& nums) {
map<int, queue<int>> occurrences;
auto sgn = [](int x) { return (x % 2) == 0 ? 1 : -1; };
int len = 0;
vector<int> prefix_sum(nums.size(), 0);
prefix_sum[0] = sgn(nums[0]);
occurrences[nums[0]].push(1);
for (int i = 1; i < nums.size(); i++) {
prefix_sum[i] = prefix_sum[i - 1];
auto& occ = occurrences[nums[i]];
if (occ.empty()) {
prefix_sum[i] += sgn(nums[i]);
}
occ.push(i + 1);
}
SegmentTree seg(prefix_sum);
for (int i = 0; i < nums.size(); i++) {
len = std::max(len, seg.find_last(i + len, 0) - i);
auto next_pos = nums.size() + 1;
occurrences[nums[i]].pop();
if (!occurrences[nums[i]].empty()) {
next_pos = occurrences[nums[i]].front();
}
seg.add(i + 1, next_pos - 1, -sgn(nums[i]));
}
return len;
}
};
###JavaScript
class LazyTag {
constructor() {
this.toAdd = 0;
}
add(other) {
this.toAdd += other.toAdd;
return this;
}
hasTag() {
return this.toAdd !== 0;
}
clear() {
this.toAdd = 0;
}
}
class SegmentTreeNode {
constructor() {
this.minValue = 0;
this.maxValue = 0;
// int data = 0; // 只有叶子节点使用, 本题不需要
this.lazyTag = new LazyTag();
}
}
class SegmentTree {
constructor(data) {
this.n = data.length;
this.tree = new Array(this.n * 4 + 1).fill(null).map(() => new SegmentTreeNode());
this.build(data, 1, this.n, 1);
}
add(l, r, val) {
const tag = new LazyTag();
tag.toAdd = val;
this.update(l, r, tag, 1, this.n, 1);
}
findLast(start, val) {
if (start > this.n) {
return -1;
}
return this.find(start, this.n, val, 1, this.n, 1);
}
applyTag(i, tag) {
this.tree[i].minValue += tag.toAdd;
this.tree[i].maxValue += tag.toAdd;
this.tree[i].lazyTag.add(tag);
}
pushdown(i) {
if (this.tree[i].lazyTag.hasTag()) {
const tag = new LazyTag();
tag.toAdd = this.tree[i].lazyTag.toAdd;
this.applyTag(i << 1, tag);
this.applyTag((i << 1) | 1, tag);
this.tree[i].lazyTag.clear();
}
}
pushup(i) {
this.tree[i].minValue = Math.min(this.tree[i << 1].minValue, this.tree[(i << 1) | 1].minValue);
this.tree[i].maxValue = Math.max(this.tree[i << 1].maxValue, this.tree[(i << 1) | 1].maxValue);
}
build(data, l, r, i) {
if (l == r) {
this.tree[i].minValue = this.tree[i].maxValue = data[l - 1];
return;
}
const mid = l + ((r - l) >> 1);
this.build(data, l, mid, i << 1);
this.build(data, mid + 1, r, (i << 1) | 1);
this.pushup(i);
}
update(targetL, targetR, tag, l, r, i) {
if (targetL <= l && r <= targetR) {
this.applyTag(i, tag);
return;
}
this.pushdown(i);
const mid = l + ((r - l) >> 1);
if (targetL <= mid)
this.update(targetL, targetR, tag, l, mid, i << 1);
if (targetR > mid)
this.update(targetL, targetR, tag, mid + 1, r, (i << 1) | 1);
this.pushup(i);
}
find(targetL, targetR, val, l, r, i) {
if (this.tree[i].minValue > val || this.tree[i].maxValue < val) {
return -1;
}
// 根据介值定理,此时区间内必然存在解
if (l == r) {
return l;
}
this.pushdown(i);
const mid = l + ((r - l) >> 1);
// targetL 一定小于等于 r(=n)
if (targetR >= mid + 1) {
const res = this.find(targetL, targetR, val, mid + 1, r, (i << 1) | 1);
if (res != -1)
return res;
}
if (l <= targetR && mid >= targetL) {
return this.find(targetL, targetR, val, l, mid, i << 1);
}
return -1;
}
}
var longestBalanced = function(nums) {
const occurrences = new Map();
const sgn = (x) => (x % 2 == 0 ? 1 : -1);
let len = 0;
const prefixSum = new Array(nums.length).fill(0);
prefixSum[0] = sgn(nums[0]);
if (!occurrences.has(nums[0])) occurrences.set(nums[0], new Queue());
occurrences.get(nums[0]).push(1);
for (let i = 1; i < nums.length; i++) {
prefixSum[i] = prefixSum[i - 1];
if (!occurrences.has(nums[i]))
occurrences.set(nums[i], new Queue());
const occ = occurrences.get(nums[i]);
if (occ.size() === 0) {
prefixSum[i] += sgn(nums[i]);
}
occ.push(i + 1);
}
const seg = new SegmentTree(prefixSum);
for (let i = 0; i < nums.length; i++) {
len = Math.max(len, seg.findLast(i + len, 0) - i);
let nextPos = nums.length + 1;
const occ = occurrences.get(nums[i]);
occ.pop();
if (occ.size() > 0) {
nextPos = occ.front();
}
seg.add(i + 1, nextPos - 1, -sgn(nums[i]));
}
return len;
}
###TypeScript
class LazyTag {
toAdd: number = 0;
add(other: LazyTag): LazyTag {
this.toAdd += other.toAdd;
return this;
}
hasTag(): boolean {
return this.toAdd !== 0;
}
clear(): void {
this.toAdd = 0;
}
}
class SegmentTreeNode {
minValue: number = 0;
maxValue: number = 0;
// int data = 0; // 只有叶子节点使用, 本题不需要
lazyTag: LazyTag = new LazyTag();
}
class SegmentTree {
n: number;
tree: SegmentTreeNode[];
constructor(data: number[]) {
this.n = data.length;
this.tree = new Array(this.n * 4 + 1).fill(null).map(() => new SegmentTreeNode());
this.build(data, 1, this.n, 1);
}
add(l: number, r: number, val: number): void {
const tag = new LazyTag();
tag.toAdd = val;
this.update(l, r, tag, 1, this.n, 1);
}
findLast(start: number, val: number): number {
if (start > this.n) {
return -1;
}
return this.find(start, this.n, val, 1, this.n, 1);
}
private applyTag(i: number, tag: LazyTag): void {
this.tree[i].minValue += tag.toAdd;
this.tree[i].maxValue += tag.toAdd;
this.tree[i].lazyTag.add(tag);
}
private pushdown(i: number): void {
if (this.tree[i].lazyTag.hasTag()) {
const tag = new LazyTag();
tag.toAdd = this.tree[i].lazyTag.toAdd;
this.applyTag(i << 1, tag);
this.applyTag((i << 1) | 1, tag);
this.tree[i].lazyTag.clear();
}
}
private pushup(i: number): void {
this.tree[i].minValue = Math.min(
this.tree[i << 1].minValue,
this.tree[(i << 1) | 1].minValue,
);
this.tree[i].maxValue = Math.max(
this.tree[i << 1].maxValue,
this.tree[(i << 1) | 1].maxValue,
);
}
private build(data: number[], l: number, r: number, i: number): void {
if (l == r) {
this.tree[i].minValue = this.tree[i].maxValue = data[l - 1];
return;
}
const mid = l + ((r - l) >> 1);
this.build(data, l, mid, i << 1);
this.build(data, mid + 1, r, (i << 1) | 1);
this.pushup(i);
}
private update(
targetL: number,
targetR: number,
tag: LazyTag,
l: number,
r: number,
i: number,
): void {
if (targetL <= l && r <= targetR) {
this.applyTag(i, tag);
return;
}
this.pushdown(i);
const mid = l + ((r - l) >> 1);
if (targetL <= mid) this.update(targetL, targetR, tag, l, mid, i << 1);
if (targetR > mid) this.update(targetL, targetR, tag, mid + 1, r, (i << 1) | 1);
this.pushup(i);
}
private find(
targetL: number,
targetR: number,
val: number,
l: number,
r: number,
i: number,
): number {
if (this.tree[i].minValue > val || this.tree[i].maxValue < val) {
return -1;
}
// 根据介值定理,此时区间内必然存在解
if (l == r) {
return l;
}
this.pushdown(i);
const mid = l + ((r - l) >> 1);
// targetL 一定小于等于 r(=n)
if (targetR >= mid + 1) {
const res = this.find(targetL, targetR, val, mid + 1, r, (i << 1) | 1);
if (res != -1) return res;
}
if (l <= targetR && mid >= targetL) {
return this.find(targetL, targetR, val, l, mid, i << 1);
}
return -1;
}
}
function longestBalanced(nums: number[]): number {
const occurrences = new Map<number, Queue<number>>();
const sgn = (x: number) => (x % 2 == 0 ? 1 : -1);
let len = 0;
const prefixSum: number[] = new Array(nums.length).fill(0);
prefixSum[0] = sgn(nums[0]);
if (!occurrences.has(nums[0])) occurrences.set(nums[0], new Queue());
occurrences.get(nums[0])!.push(1);
for (let i = 1; i < nums.length; i++) {
prefixSum[i] = prefixSum[i - 1];
if (!occurrences.has(nums[i])) occurrences.set(nums[i], new Queue());
const occ = occurrences.get(nums[i])!;
if (occ.size() === 0) {
prefixSum[i] += sgn(nums[i]);
}
occ.push(i + 1);
}
const seg = new SegmentTree(prefixSum);
for (let i = 0; i < nums.length; i++) {
len = Math.max(len, seg.findLast(i + len, 0) - i);
let nextPos = nums.length + 1;
const occ = occurrences.get(nums[i])!;
occ.pop();
if (occ.size() > 0) {
nextPos = occ.front();
}
seg.add(i + 1, nextPos - 1, -sgn(nums[i]));
}
return len;
}
###Java
class LazyTag {
int toAdd;
LazyTag() {
this.toAdd = 0;
}
LazyTag add(LazyTag other) {
this.toAdd += other.toAdd;
return this;
}
boolean hasTag() {
return this.toAdd != 0;
}
void clear() {
this.toAdd = 0;
}
}
class SegmentTreeNode {
int minValue;
int maxValue;
LazyTag lazyTag;
SegmentTreeNode() {
this.minValue = 0;
this.maxValue = 0;
this.lazyTag = new LazyTag();
}
}
class SegmentTree {
private int n;
private SegmentTreeNode[] tree;
SegmentTree(int[] data) {
this.n = data.length;
this.tree = new SegmentTreeNode[this.n * 4 + 1];
for (int i = 0; i < tree.length; i++) {
tree[i] = new SegmentTreeNode();
}
build(data, 1, this.n, 1);
}
void add(int l, int r, int val) {
LazyTag tag = new LazyTag();
tag.toAdd = val;
update(l, r, tag, 1, this.n, 1);
}
int findLast(int start, int val) {
if (start > this.n) {
return -1;
}
return find(start, this.n, val, 1, this.n, 1);
}
private void applyTag(int i, LazyTag tag) {
tree[i].minValue += tag.toAdd;
tree[i].maxValue += tag.toAdd;
tree[i].lazyTag.add(tag);
}
private void pushdown(int i) {
if (tree[i].lazyTag.hasTag()) {
LazyTag tag = new LazyTag();
tag.toAdd = tree[i].lazyTag.toAdd;
applyTag(i << 1, tag);
applyTag((i << 1) | 1, tag);
tree[i].lazyTag.clear();
}
}
private void pushup(int i) {
tree[i].minValue = Math.min(tree[i << 1].minValue, tree[(i << 1) | 1].minValue);
tree[i].maxValue = Math.max(tree[i << 1].maxValue, tree[(i << 1) | 1].maxValue);
}
private void build(int[] data, int l, int r, int i) {
if (l == r) {
tree[i].minValue = tree[i].maxValue = data[l - 1];
return;
}
int mid = l + ((r - l) >> 1);
build(data, l, mid, i << 1);
build(data, mid + 1, r, (i << 1) | 1);
pushup(i);
}
private void update(int targetL, int targetR, LazyTag tag, int l, int r, int i) {
if (targetL <= l && r <= targetR) {
applyTag(i, tag);
return;
}
pushdown(i);
int mid = l + ((r - l) >> 1);
if (targetL <= mid)
update(targetL, targetR, tag, l, mid, i << 1);
if (targetR > mid)
update(targetL, targetR, tag, mid + 1, r, (i << 1) | 1);
pushup(i);
}
private int find(int targetL, int targetR, int val, int l, int r, int i) {
if (tree[i].minValue > val || tree[i].maxValue < val) {
return -1;
}
if (l == r) {
return l;
}
pushdown(i);
int mid = l + ((r - l) >> 1);
if (targetR >= mid + 1) {
int res = find(targetL, targetR, val, mid + 1, r, (i << 1) | 1);
if (res != -1)
return res;
}
if (l <= targetR && mid >= targetL) {
return find(targetL, targetR, val, l, mid, i << 1);
}
return -1;
}
}
class Solution {
public int longestBalanced(int[] nums) {
Map<Integer, Queue<Integer>> occurrences = new HashMap<>();
int len = 0;
int[] prefixSum = new int[nums.length];
prefixSum[0] = sgn(nums[0]);
occurrences.computeIfAbsent(nums[0], k -> new LinkedList<>()).add(1);
for (int i = 1; i < nums.length; i++) {
prefixSum[i] = prefixSum[i - 1];
Queue<Integer> occ = occurrences.computeIfAbsent(nums[i], k -> new LinkedList<>());
if (occ.isEmpty()) {
prefixSum[i] += sgn(nums[i]);
}
occ.add(i + 1);
}
SegmentTree seg = new SegmentTree(prefixSum);
for (int i = 0; i < nums.length; i++) {
len = Math.max(len, seg.findLast(i + len, 0) - i);
int nextPos = nums.length + 1;
occurrences.get(nums[i]).poll();
if (!occurrences.get(nums[i]).isEmpty()) {
nextPos = occurrences.get(nums[i]).peek();
}
seg.add(i + 1, nextPos - 1, -sgn(nums[i]));
}
return len;
}
private int sgn(int x) {
return (x % 2) == 0 ? 1 : -1;
}
}
###C#
public class LazyTag {
public int toAdd;
public LazyTag() {
this.toAdd = 0;
}
public LazyTag Add(LazyTag other) {
this.toAdd += other.toAdd;
return this;
}
public bool HasTag() {
return this.toAdd != 0;
}
public void Clear() {
this.toAdd = 0;
}
}
public class SegmentTreeNode {
public int minValue;
public int maxValue;
public LazyTag lazyTag;
public SegmentTreeNode() {
this.minValue = 0;
this.maxValue = 0;
this.lazyTag = new LazyTag();
}
}
public class SegmentTree {
private int n;
private SegmentTreeNode[] tree;
public SegmentTree(int[] data) {
this.n = data.Length;
this.tree = new SegmentTreeNode[this.n * 4 + 1];
for (int i = 0; i < tree.Length; i++) {
tree[i] = new SegmentTreeNode();
}
Build(data, 1, this.n, 1);
}
public void Add(int l, int r, int val) {
LazyTag tag = new LazyTag();
tag.toAdd = val;
Update(l, r, tag, 1, this.n, 1);
}
public int FindLast(int start, int val) {
if (start > this.n) {
return -1;
}
return Find(start, this.n, val, 1, this.n, 1);
}
private void ApplyTag(int i, LazyTag tag) {
tree[i].minValue += tag.toAdd;
tree[i].maxValue += tag.toAdd;
tree[i].lazyTag.Add(tag);
}
private void Pushdown(int i) {
if (tree[i].lazyTag.HasTag()) {
LazyTag tag = new LazyTag();
tag.toAdd = tree[i].lazyTag.toAdd;
ApplyTag(i << 1, tag);
ApplyTag((i << 1) | 1, tag);
tree[i].lazyTag.Clear();
}
}
private void Pushup(int i) {
tree[i].minValue = Math.Min(tree[i << 1].minValue, tree[(i << 1) | 1].minValue);
tree[i].maxValue = Math.Max(tree[i << 1].maxValue, tree[(i << 1) | 1].maxValue);
}
private void Build(int[] data, int l, int r, int i) {
if (l == r) {
tree[i].minValue = tree[i].maxValue = data[l - 1];
return;
}
int mid = l + ((r - l) >> 1);
Build(data, l, mid, i << 1);
Build(data, mid + 1, r, (i << 1) | 1);
Pushup(i);
}
private void Update(int targetL, int targetR, LazyTag tag, int l, int r, int i) {
if (targetL <= l && r <= targetR) {
ApplyTag(i, tag);
return;
}
Pushdown(i);
int mid = l + ((r - l) >> 1);
if (targetL <= mid)
Update(targetL, targetR, tag, l, mid, i << 1);
if (targetR > mid)
Update(targetL, targetR, tag, mid + 1, r, (i << 1) | 1);
Pushup(i);
}
private int Find(int targetL, int targetR, int val, int l, int r, int i) {
if (tree[i].minValue > val || tree[i].maxValue < val) {
return -1;
}
if (l == r) {
return l;
}
Pushdown(i);
int mid = l + ((r - l) >> 1);
if (targetR >= mid + 1) {
int res = Find(targetL, targetR, val, mid + 1, r, (i << 1) | 1);
if (res != -1)
return res;
}
if (l <= targetR && mid >= targetL) {
return Find(targetL, targetR, val, l, mid, i << 1);
}
return -1;
}
}
public class Solution {
public int LongestBalanced(int[] nums) {
var occurrences = new Dictionary<int, Queue<int>>();
int len = 0;
int[] prefixSum = new int[nums.Length];
prefixSum[0] = Sgn(nums[0]);
if (!occurrences.ContainsKey(nums[0])) {
occurrences[nums[0]] = new Queue<int>();
}
occurrences[nums[0]].Enqueue(1);
for (int i = 1; i < nums.Length; i++) {
prefixSum[i] = prefixSum[i - 1];
if (!occurrences.ContainsKey(nums[i])) {
occurrences[nums[i]] = new Queue<int>();
}
var occ = occurrences[nums[i]];
if (occ.Count == 0) {
prefixSum[i] += Sgn(nums[i]);
}
occ.Enqueue(i + 1);
}
var seg = new SegmentTree(prefixSum);
for (int i = 0; i < nums.Length; i++) {
len = Math.Max(len, seg.FindLast(i + len, 0) - i);
int nextPos = nums.Length + 1;
occurrences[nums[i]].Dequeue();
if (occurrences[nums[i]].Count > 0) {
nextPos = occurrences[nums[i]].Peek();
}
seg.Add(i + 1, nextPos - 1, -Sgn(nums[i]));
}
return len;
}
private int Sgn(int x) {
return (x % 2) == 0 ? 1 : -1;
}
}
###Python
class LazyTag:
def __init__(self):
self.to_add = 0
def add(self, other):
self.to_add += other.to_add
return self
def has_tag(self):
return self.to_add != 0
def clear(self):
self.to_add = 0
class SegmentTreeNode:
def __init__(self):
self.min_value = 0
self.max_value = 0
self.lazy_tag = LazyTag()
class SegmentTree:
def __init__(self, data):
self.n = len(data)
self.tree = [SegmentTreeNode() for _ in range(self.n * 4 + 1)]
self._build(data, 1, self.n, 1)
def add(self, l, r, val):
tag = LazyTag()
tag.to_add = val
self._update(l, r, tag, 1, self.n, 1)
def find_last(self, start, val):
if start > self.n:
return -1
return self._find(start, self.n, val, 1, self.n, 1)
def _apply_tag(self, i, tag):
self.tree[i].min_value += tag.to_add
self.tree[i].max_value += tag.to_add
self.tree[i].lazy_tag.add(tag)
def _pushdown(self, i):
if self.tree[i].lazy_tag.has_tag():
tag = LazyTag()
tag.to_add = self.tree[i].lazy_tag.to_add
self._apply_tag(i << 1, tag)
self._apply_tag((i << 1) | 1, tag)
self.tree[i].lazy_tag.clear()
def _pushup(self, i):
self.tree[i].min_value = min(self.tree[i << 1].min_value,
self.tree[(i << 1) | 1].min_value)
self.tree[i].max_value = max(self.tree[i << 1].max_value,
self.tree[(i << 1) | 1].max_value)
def _build(self, data, l, r, i):
if l == r:
self.tree[i].min_value = data[l - 1]
self.tree[i].max_value = data[l - 1]
return
mid = l + ((r - l) >> 1)
self._build(data, l, mid, i << 1)
self._build(data, mid + 1, r, (i << 1) | 1)
self._pushup(i)
def _update(self, target_l, target_r, tag, l, r, i):
if target_l <= l and r <= target_r:
self._apply_tag(i, tag)
return
self._pushdown(i)
mid = l + ((r - l) >> 1)
if target_l <= mid:
self._update(target_l, target_r, tag, l, mid, i << 1)
if target_r > mid:
self._update(target_l, target_r, tag, mid + 1, r, (i << 1) | 1)
self._pushup(i)
def _find(self, target_l, target_r, val, l, r, i):
if self.tree[i].min_value > val or self.tree[i].max_value < val:
return -1
if l == r:
return l
self._pushdown(i)
mid = l + ((r - l) >> 1)
if target_r >= mid + 1:
res = self._find(target_l, target_r, val, mid + 1, r, (i << 1) | 1)
if res != -1:
return res
if l <= target_r and mid >= target_l:
return self._find(target_l, target_r, val, l, mid, i << 1)
return -1
class Solution:
def longestBalanced(self, nums: List[int]) -> int:
occurrences = defaultdict(deque)
def sgn(x):
return 1 if x % 2 == 0 else -1
length = 0
prefix_sum = [0] * len(nums)
prefix_sum[0] = sgn(nums[0])
occurrences[nums[0]].append(1)
for i in range(1, len(nums)):
prefix_sum[i] = prefix_sum[i - 1]
occ = occurrences[nums[i]]
if not occ:
prefix_sum[i] += sgn(nums[i])
occ.append(i + 1)
seg = SegmentTree(prefix_sum)
for i in range(len(nums)):
length = max(length, seg.find_last(i + length, 0) - i)
next_pos = len(nums) + 1
occurrences[nums[i]].popleft()
if occurrences[nums[i]]:
next_pos = occurrences[nums[i]][0]
seg.add(i + 1, next_pos - 1, -sgn(nums[i]))
return length
###Go
type LazyTag struct {
toAdd int
}
func (l *LazyTag) Add(other *LazyTag) *LazyTag {
l.toAdd += other.toAdd
return l
}
func (l *LazyTag) HasTag() bool {
return l.toAdd != 0
}
func (l *LazyTag) Clear() {
l.toAdd = 0
}
type SegmentTreeNode struct {
minValue int
maxValue int
lazyTag *LazyTag
}
func NewSegmentTreeNode() *SegmentTreeNode {
return &SegmentTreeNode{
minValue: 0,
maxValue: 0,
lazyTag: &LazyTag{},
}
}
type SegmentTree struct {
n int
tree []*SegmentTreeNode
}
func NewSegmentTree(data []int) *SegmentTree {
n := len(data)
tree := make([]*SegmentTreeNode, n*4+1)
for i := range tree {
tree[i] = NewSegmentTreeNode()
}
seg := &SegmentTree{n: n, tree: tree}
seg.build(data, 1, n, 1)
return seg
}
func (seg *SegmentTree) Add(l, r, val int) {
tag := &LazyTag{toAdd: val}
seg.update(l, r, tag, 1, seg.n, 1)
}
func (seg *SegmentTree) FindLast(start, val int) int {
if start > seg.n {
return -1
}
return seg.find(start, seg.n, val, 1, seg.n, 1)
}
func (seg *SegmentTree) applyTag(i int, tag *LazyTag) {
seg.tree[i].minValue += tag.toAdd
seg.tree[i].maxValue += tag.toAdd
seg.tree[i].lazyTag.Add(tag)
}
func (seg *SegmentTree) pushdown(i int) {
if seg.tree[i].lazyTag.HasTag() {
tag := &LazyTag{toAdd: seg.tree[i].lazyTag.toAdd}
seg.applyTag(i<<1, tag)
seg.applyTag((i<<1)|1, tag)
seg.tree[i].lazyTag.Clear()
}
}
func (seg *SegmentTree) pushup(i int) {
left := seg.tree[i<<1]
right := seg.tree[(i<<1)|1]
seg.tree[i].minValue = min(left.minValue, right.minValue)
seg.tree[i].maxValue = max(left.maxValue, right.maxValue)
}
func (seg *SegmentTree) build(data []int, l, r, i int) {
if l == r {
seg.tree[i].minValue = data[l-1]
seg.tree[i].maxValue = data[l-1]
return
}
mid := l + ((r - l) >> 1)
seg.build(data, l, mid, i<<1)
seg.build(data, mid+1, r, (i<<1)|1)
seg.pushup(i)
}
func (seg *SegmentTree) update(targetL, targetR int, tag *LazyTag, l, r, i int) {
if targetL <= l && r <= targetR {
seg.applyTag(i, tag)
return
}
seg.pushdown(i)
mid := l + ((r - l) >> 1)
if targetL <= mid {
seg.update(targetL, targetR, tag, l, mid, i<<1)
}
if targetR > mid {
seg.update(targetL, targetR, tag, mid+1, r, (i<<1)|1)
}
seg.pushup(i)
}
func (seg *SegmentTree) find(targetL, targetR, val, l, r, i int) int {
if seg.tree[i].minValue > val || seg.tree[i].maxValue < val {
return -1
}
if l == r {
return l
}
seg.pushdown(i)
mid := l + ((r - l) >> 1)
if targetR >= mid+1 {
res := seg.find(targetL, targetR, val, mid+1, r, (i<<1)|1)
if res != -1 {
return res
}
}
if l <= targetR && mid >= targetL {
return seg.find(targetL, targetR, val, l, mid, i<<1)
}
return -1
}
func longestBalanced(nums []int) int {
occurrences := make(map[int][]int)
sgn := func(x int) int {
if x%2 == 0 {
return 1
}
return -1
}
length := 0
prefixSum := make([]int, len(nums))
prefixSum[0] = sgn(nums[0])
occurrences[nums[0]] = append(occurrences[nums[0]], 1)
for i := 1; i < len(nums); i++ {
prefixSum[i] = prefixSum[i-1]
occ := occurrences[nums[i]]
if len(occ) == 0 {
prefixSum[i] += sgn(nums[i])
}
occurrences[nums[i]] = append(occ, i+1)
}
seg := NewSegmentTree(prefixSum)
for i := 0; i < len(nums); i++ {
length = max(length, seg.FindLast(i+length, 0)-i)
nextPos := len(nums) + 1
occurrences[nums[i]] = occurrences[nums[i]][1:]
if len(occurrences[nums[i]]) > 0 {
nextPos = occurrences[nums[i]][0]
}
seg.Add(i+1, nextPos-1, -sgn(nums[i]))
}
return length
}
###C
typedef struct ListNode ListNode;
typedef struct {
ListNode *head;
int size;
} List;
typedef struct {
int key;
List *val;
UT_hash_handle hh;
} HashItem;
List* listCreate() {
List *list = (List*)malloc(sizeof(List));
list->head = NULL;
list->size = 0;
return list;
}
void listPush(List *list, int val) {
ListNode *node = (ListNode*)malloc(sizeof(ListNode));
node->val = val;
node->next = list->head;
list->head = node;
list->size++;
}
void listPop(List *list) {
if (list->head == NULL) return;
ListNode *temp = list->head;
list->head = list->head->next;
free(temp);
list->size--;
}
int listAt(List *list, int index) {
ListNode *cur = list->head;
for (int i = 0; i < index && cur != NULL; i++) {
cur = cur->next;
}
return cur ? cur->val : -1;
}
void listReverse(List *list) {
ListNode *prev = NULL;
ListNode *cur = list->head;
ListNode *next = NULL;
while (cur != NULL) {
next = cur->next;
cur->next = prev;
prev = cur;
cur = next;
}
list->head = prev;
}
void listFree(List *list) {
while (list->head != NULL) {
listPop(list);
}
free(list);
}
HashItem* hashFindItem(HashItem **obj, int key) {
HashItem *pEntry = NULL;
HASH_FIND_INT(*obj, &key, pEntry);
return pEntry;
}
bool hashAddItem(HashItem **obj, int key, List *val) {
if (hashFindItem(obj, key)) {
return false;
}
HashItem *pEntry = (HashItem*)malloc(sizeof(HashItem));
pEntry->key = key;
pEntry->val = val;
HASH_ADD_INT(*obj, key, pEntry);
return true;
}
List* hashGetItem(HashItem **obj, int key) {
HashItem *pEntry = hashFindItem(obj, key);
if (!pEntry) {
List *newList = listCreate();
hashAddItem(obj, key, newList);
return newList;
}
return pEntry->val;
}
void hashFree(HashItem **obj) {
HashItem *curr = NULL, *tmp = NULL;
HASH_ITER(hh, *obj, curr, tmp) {
HASH_DEL(*obj, curr);
listFree(curr->val);
free(curr);
}
}
void hashIterate(HashItem **obj, void (*callback)(HashItem *item)) {
HashItem *curr = NULL, *tmp = NULL;
HASH_ITER(hh, *obj, curr, tmp) {
callback(curr);
}
}
typedef struct {
int toAdd;
} LazyTag;
void lazyTagAdd(LazyTag *tag, LazyTag *other) {
tag->toAdd += other->toAdd;
}
bool lazyTagHasTag(LazyTag *tag) {
return tag->toAdd != 0;
}
void lazyTagClear(LazyTag *tag) {
tag->toAdd = 0;
}
typedef struct {
int minValue;
int maxValue;
LazyTag lazyTag;
} SegmentTreeNode;
typedef struct {
int n;
SegmentTreeNode *tree;
} SegmentTree;
void segmentTreeApplyTag(SegmentTree *seg, int i, LazyTag *tag) {
seg->tree[i].minValue += tag->toAdd;
seg->tree[i].maxValue += tag->toAdd;
lazyTagAdd(&seg->tree[i].lazyTag, tag);
}
void segmentTreePushdown(SegmentTree *seg, int i) {
if (lazyTagHasTag(&seg->tree[i].lazyTag)) {
LazyTag tag = {seg->tree[i].lazyTag.toAdd};
segmentTreeApplyTag(seg, i << 1, &tag);
segmentTreeApplyTag(seg, (i << 1) | 1, &tag);
lazyTagClear(&seg->tree[i].lazyTag);
}
}
void segmentTreePushup(SegmentTree *seg, int i) {
seg->tree[i].minValue = fmin(seg->tree[i << 1].minValue, seg->tree[(i << 1) | 1].minValue);
seg->tree[i].maxValue = fmax(seg->tree[i << 1].maxValue, seg->tree[(i << 1) | 1].maxValue);
}
void segmentTreeBuild(SegmentTree *seg, int *data, int l, int r, int i) {
if (l == r) {
seg->tree[i].minValue = seg->tree[i].maxValue = data[l - 1];
return;
}
int mid = l + ((r - l) >> 1);
segmentTreeBuild(seg, data, l, mid, i << 1);
segmentTreeBuild(seg, data, mid + 1, r, (i << 1) | 1);
segmentTreePushup(seg, i);
}
void segmentTreeUpdate(SegmentTree *seg, int targetL, int targetR, LazyTag *tag,
int l, int r, int i) {
if (targetL <= l && r <= targetR) {
segmentTreeApplyTag(seg, i, tag);
return;
}
segmentTreePushdown(seg, i);
int mid = l + ((r - l) >> 1);
if (targetL <= mid) {
segmentTreeUpdate(seg, targetL, targetR, tag, l, mid, i << 1);
}
if (targetR > mid) {
segmentTreeUpdate(seg, targetL, targetR, tag, mid + 1, r, (i << 1) | 1);
}
segmentTreePushup(seg, i);
}
int segmentTreeFind(SegmentTree *seg, int targetL, int targetR, int val,
int l, int r, int i) {
if (seg->tree[i].minValue > val || seg->tree[i].maxValue < val) {
return -1;
}
if (l == r) {
return l;
}
segmentTreePushdown(seg, i);
int mid = l + ((r - l) >> 1);
if (targetR >= mid + 1) {
int res = segmentTreeFind(seg, targetL, targetR, val, mid + 1, r, (i << 1) | 1);
if (res != -1) {
return res;
}
}
if (targetL <= mid) {
return segmentTreeFind(seg, targetL, targetR, val, l, mid, i << 1);
}
return -1;
}
SegmentTree* segmentTreeCreate(int *data, int n) {
SegmentTree *seg = (SegmentTree*)malloc(sizeof(SegmentTree));
seg->n = n;
seg->tree = (SegmentTreeNode*)calloc(n * 4 + 1, sizeof(SegmentTreeNode));
segmentTreeBuild(seg, data, 1, n, 1);
return seg;
}
void segmentTreeAdd(SegmentTree *seg, int l, int r, int val) {
LazyTag tag = {val};
segmentTreeUpdate(seg, l, r, &tag, 1, seg->n, 1);
}
int segmentTreeFindLast(SegmentTree *seg, int start, int val) {
if (start > seg->n) {
return -1;
}
return segmentTreeFind(seg, start, seg->n, val, 1, seg->n, 1);
}
void segmentTreeFree(SegmentTree *seg) {
free(seg->tree);
free(seg);
}
int sgn(int x) {
return (x % 2 == 0) ? 1 : -1;
}
void reverseList(HashItem *item) {
listReverse(item->val);
}
int longestBalanced(int* nums, int numsSize) {
HashItem *occurrences = NULL;
int len = 0;
int *prefixSum = (int*)calloc(numsSize, sizeof(int));
prefixSum[0] = sgn(nums[0]);
List *list0 = hashGetItem(&occurrences, nums[0]);
listPush(list0, 1);
for (int i = 1; i < numsSize; i++) {
prefixSum[i] = prefixSum[i - 1];
List *occ = hashGetItem(&occurrences, nums[i]);
if (occ->size == 0) {
prefixSum[i] += sgn(nums[i]);
}
listPush(occ, i + 1);
}
hashIterate(&occurrences, reverseList);
SegmentTree *seg = segmentTreeCreate(prefixSum, numsSize);
for (int i = 0; i < numsSize; i++) {
int findResult = segmentTreeFindLast(seg, i + len, 0);
int newLen = findResult - i;
if (newLen > len) {
len = newLen;
}
int nextPos = numsSize + 1;
List *occ = hashGetItem(&occurrences, nums[i]);
listPop(occ);
if (occ->size > 0) {
nextPos = listAt(occ, 0);
}
segmentTreeAdd(seg, i + 1, nextPos - 1, -sgn(nums[i]));
}
segmentTreeFree(seg);
free(prefixSum);
hashFree(&occurrences);
return len;
}
###Rust
use std::collections::{HashMap, VecDeque};
use std::cmp::max;
#[derive(Debug, Clone, Copy)]
struct LazyTag {
add: i32,
}
impl LazyTag {
fn new() -> Self {
LazyTag { add: 0 }
}
fn is_empty(&self) -> bool {
self.add == 0
}
fn combine(&mut self, other: &LazyTag) {
self.add += other.add;
}
fn clear(&mut self) {
self.add = 0;
}
}
#[derive(Debug, Clone)]
struct Node {
min_val: i32,
max_val: i32,
lazy: LazyTag,
}
impl Node {
fn new() -> Self {
Node {
min_val: 0,
max_val: 0,
lazy: LazyTag::new(),
}
}
}
struct SegmentTree {
n: usize,
tree: Vec<Node>,
}
impl SegmentTree {
fn new(data: &[i32]) -> Self {
let n = data.len();
let mut tree = vec![Node::new(); 4 * n];
let mut seg = SegmentTree { n, tree };
seg.build(data, 1, n, 1);
seg
}
fn build(&mut self, data: &[i32], l: usize, r: usize, idx: usize) {
if l == r {
self.tree[idx].min_val = data[l - 1];
self.tree[idx].max_val = data[l - 1];
return;
}
let mid = (l + r) / 2;
self.build(data, l, mid, idx * 2);
self.build(data, mid + 1, r, idx * 2 + 1);
self.push_up(idx);
}
fn push_up(&mut self, idx: usize) {
let left_min = self.tree[idx * 2].min_val;
let left_max = self.tree[idx * 2].max_val;
let right_min = self.tree[idx * 2 + 1].min_val;
let right_max = self.tree[idx * 2 + 1].max_val;
self.tree[idx].min_val = left_min.min(right_min);
self.tree[idx].max_val = left_max.max(right_max);
}
fn apply(&mut self, idx: usize, tag: &LazyTag) {
self.tree[idx].min_val += tag.add;
self.tree[idx].max_val += tag.add;
self.tree[idx].lazy.combine(tag);
}
fn push_down(&mut self, idx: usize) {
if self.tree[idx].lazy.is_empty() {
return;
}
let tag = self.tree[idx].lazy;
self.apply(idx * 2, &tag);
self.apply(idx * 2 + 1, &tag);
self.tree[idx].lazy.clear();
}
fn range_add(&mut self, l: usize, r: usize, val: i32) {
if l > r || l > self.n || r < 1 {
return;
}
let tag = LazyTag { add: val };
self._update(l, r, &tag, 1, self.n, 1);
}
fn _update(&mut self, ql: usize, qr: usize, tag: &LazyTag,
l: usize, r: usize, idx: usize) {
if ql > r || qr < l {
return;
}
if ql <= l && r <= qr {
self.apply(idx, tag);
return;
}
self.push_down(idx);
let mid = (l + r) / 2;
if ql <= mid {
self._update(ql, qr, tag, l, mid, idx * 2);
}
if qr > mid {
self._update(ql, qr, tag, mid + 1, r, idx * 2 + 1);
}
self.push_up(idx);
}
fn find_last_zero(&mut self, start: usize, val: i32) -> i32 {
if start > self.n {
return -1;
}
self._find(start, self.n, val, 1, self.n, 1)
}
fn _find(&mut self, ql: usize, qr: usize, val: i32,
l: usize, r: usize, idx: usize) -> i32 {
if l > qr || r < ql || self.tree[idx].min_val > val || self.tree[idx].max_val < val {
return -1;
}
if l == r {
return l as i32;
}
self.push_down(idx);
let mid = (l + r) / 2;
let right_res = self._find(ql, qr, val, mid + 1, r, idx * 2 + 1);
if right_res != -1 {
return right_res;
}
self._find(ql, qr, val, l, mid, idx * 2)
}
fn query_min(&self, l: usize, r: usize) -> i32 {
self._query_min(l, r, 1, self.n, 1)
}
fn _query_min(&self, ql: usize, qr: usize, l: usize, r: usize, idx: usize) -> i32 {
if ql > r || qr < l {
return i32::MAX;
}
if ql <= l && r <= qr {
return self.tree[idx].min_val;
}
let mid = (l + r) / 2;
let left_min = self._query_min(ql, qr, l, mid, idx * 2);
let right_min = self._query_min(ql, qr, mid + 1, r, idx * 2 + 1);
left_min.min(right_min)
}
}
impl Solution {
pub fn longest_balanced(nums: Vec<i32>) -> i32 {
let n = nums.len();
if n == 0 {
return 0;
}
fn sign(x: i32) -> i32 {
if x % 2 == 0 { 1 } else { -1 }
}
let mut prefix_sum = vec![0; n];
prefix_sum[0] = sign(nums[0]);
let mut pos_map: HashMap<i32, VecDeque<usize>> = HashMap::new();
pos_map.entry(nums[0]).or_insert_with(VecDeque::new).push_back(1);
for i in 1..n {
prefix_sum[i] = prefix_sum[i - 1];
let positions = pos_map.entry(nums[i]).or_insert_with(VecDeque::new);
if positions.is_empty() {
prefix_sum[i] += sign(nums[i]);
}
positions.push_back(i + 1);
}
let mut seg_tree = SegmentTree::new(&prefix_sum);
let mut max_len = 0;
for i in 0..n {
let start_idx = i + max_len as usize;
if start_idx < n {
let last_pos = seg_tree.find_last_zero(start_idx + 1, 0);
if last_pos != -1 {
max_len = max(max_len, last_pos - i as i32);
}
}
let num = nums[i];
let next_pos = pos_map.get_mut(&num)
.and_then(|positions| {
positions.pop_front();
positions.front().copied()
})
.unwrap_or(n + 2);
let delta = -sign(num);
if i + 1 <= next_pos - 1 {
seg_tree.range_add(i + 1, next_pos - 1, delta);
}
}
max_len
}
}
复杂度分析
-
时间复杂度:$O(n \log n)$,其中 $n$ 是 $\textit{nums}$ 的长度。预处理元素出现下标以及前缀和需要 $O(n \log n)$,线段树建树需要 $O(n \log n)$,后续遍历寻找合法区间需要 $O(n)$,循环内读取映射集需要 $O(\log n)$,使用线段树进行上界查找和区间加都需要 $O(\log n)$,故主循环需要 $O(n \log n)$。最后总时间复杂度为 $O(n \log n)$。
-
空间复杂度:$O(n)$。线段树需要 $O(n)$ 的空间,队列和映射集总计需要 $O(n)$ 的空间。
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
> ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>