《黑神话》中画质,1080P 分辨率,插帧帧率 90 上下。
能跑出这样的表现,你或许会觉得,高低也得是张 RTX 3060 显卡吧?
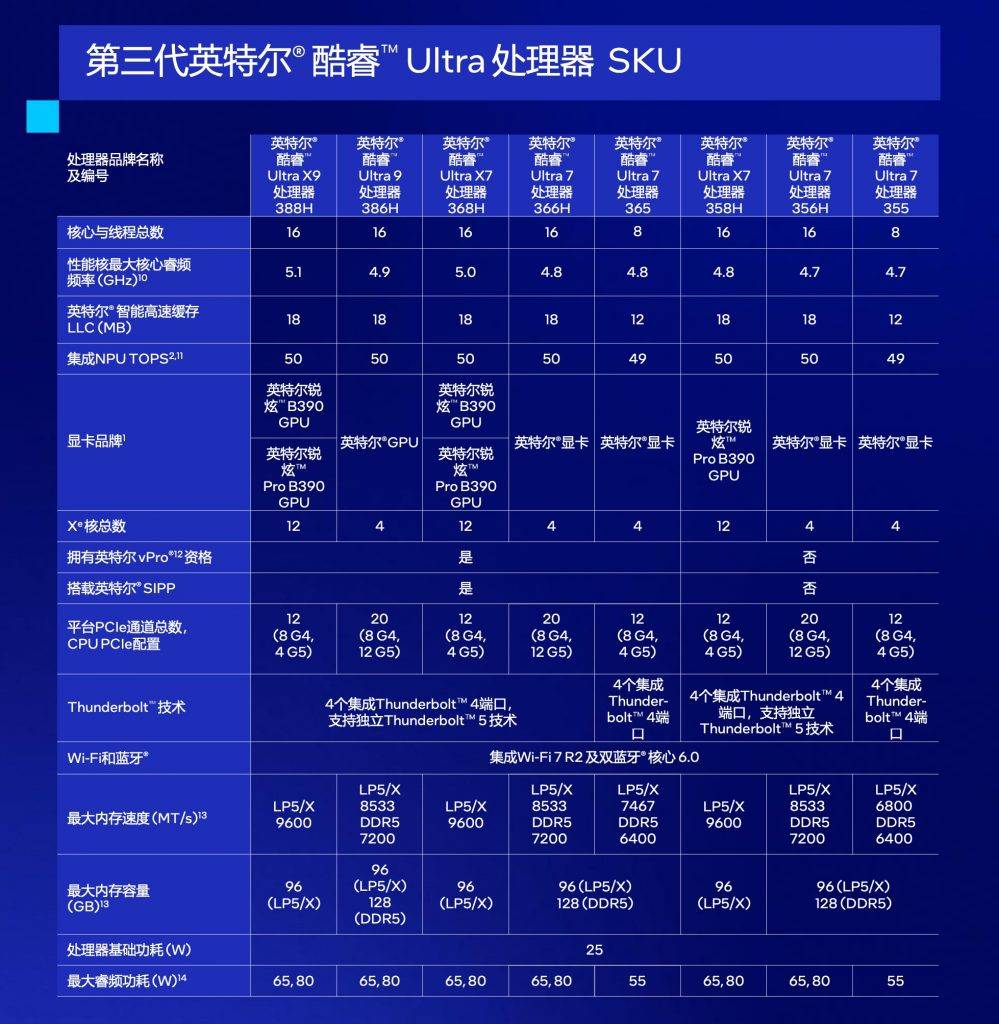
但其实,我用的是一台定位「便携」笔记本——联想小新 Pro 16 GT AI 元启版,搭载英特尔酷睿 Ultra X9 388H,12 核心 Xe3 GPU,32 GB 运行内存。

经过一周的体验,这颗使用「Panther Lake」平台 、采用英特尔最新 2nm 制程「18A」打造的芯片,确实给我们带来了 PC 产品久违的惊喜。
便携、续航、性能,全都要
虽然换用了一颗很强的芯片,但 2026 款的联想小新 16 Pro GT 还是沿用了这个老模具,除了芯片之外最大的亮点是这个 2.8K 的 120Hz OLED 屏幕,峰值亮度达到 1100nits,玩游戏的 HDR 效果堪比「闪光弹」。

作为一颗专门为移动平台打造的处理器,388H 首先在续航表现上给了我惊艳的感觉。
即使不打开「最佳能效」,用「平衡模式」进行日常办公,这台 99.9Wh 大电池的联想小新,也能坚持差不多 8 小时的持续办公时间,满电带上班能用一天。

▲ 数字稍微夸张了一点,但 9% 用个 40 分钟没问题
作为对比,我平时办公使用的 M3 MacBook Air,同样的日常办公流程,大概只能连续办公 6 小时左右,差不多下午四点多就必须要充电了。
不过,两台电脑的尺寸、电池、屏幕各不相同,对比结果仅供参考。
GPU 图形性能的表现,更是第三代酷睿 Ultra 处理器的重头戏。
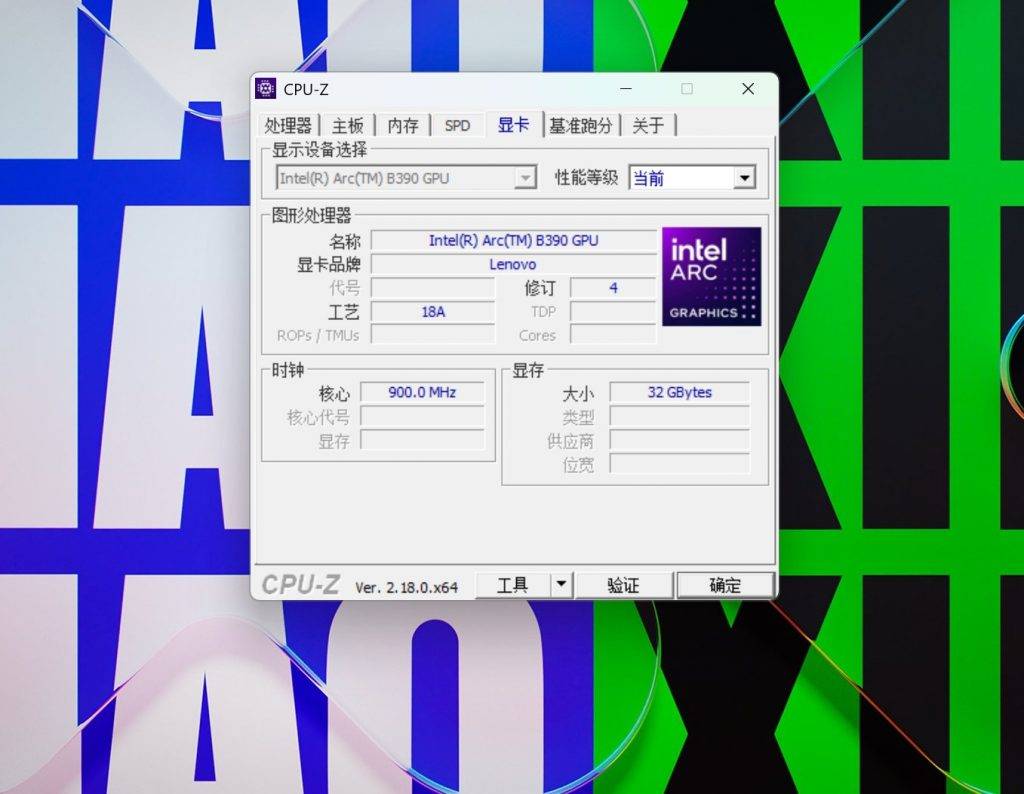
要知道,联想小新系列一直以来都是轻薄便携的性价比定位,主要面向学生和商务人群,和「3A 游戏」这个词基本无缘。
而在酷睿 Ultra X9 388H,特别是这个 12 核 Xe3 GPU 的加持下,毫不夸张的说,这台「轻薄本」几乎有着等同于 3060 显卡,或者说 PS5 主机级别的游戏能力。
并且不管是跑分还是实际的游戏体验,这台电脑的离电和接电表现几乎可以说没有差距,甚至互有胜负。
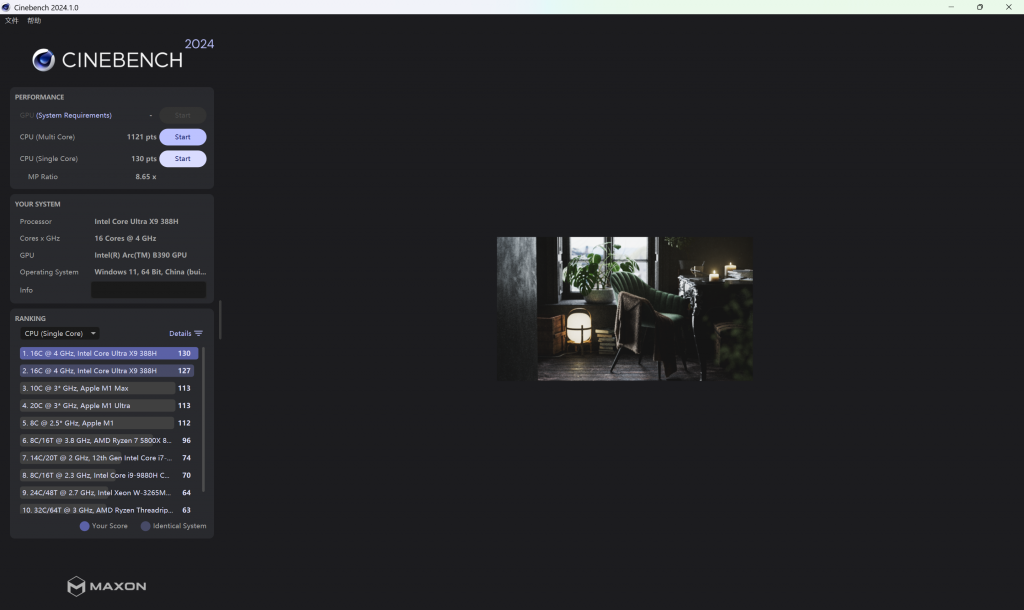
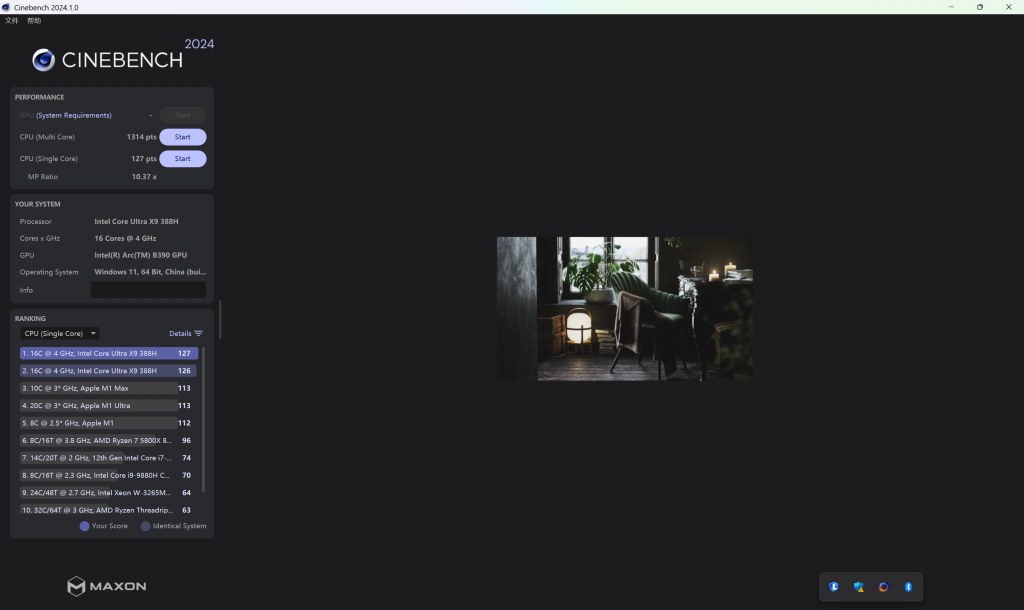
Cinebench R24 中,388H CPU 离电单核跑分 130,多核跑分 1121,连电单核 127,多核 1314。
3D Mark 的 Time Spy 环节,388H 的离电得分为 7856 分(GPU 分 7207分,CPU 分 16054),连电得分为 7896 分(GPU 分 7240分,CPU 分 16240),这个水平确实与 3060 入门级游戏本水平相当。
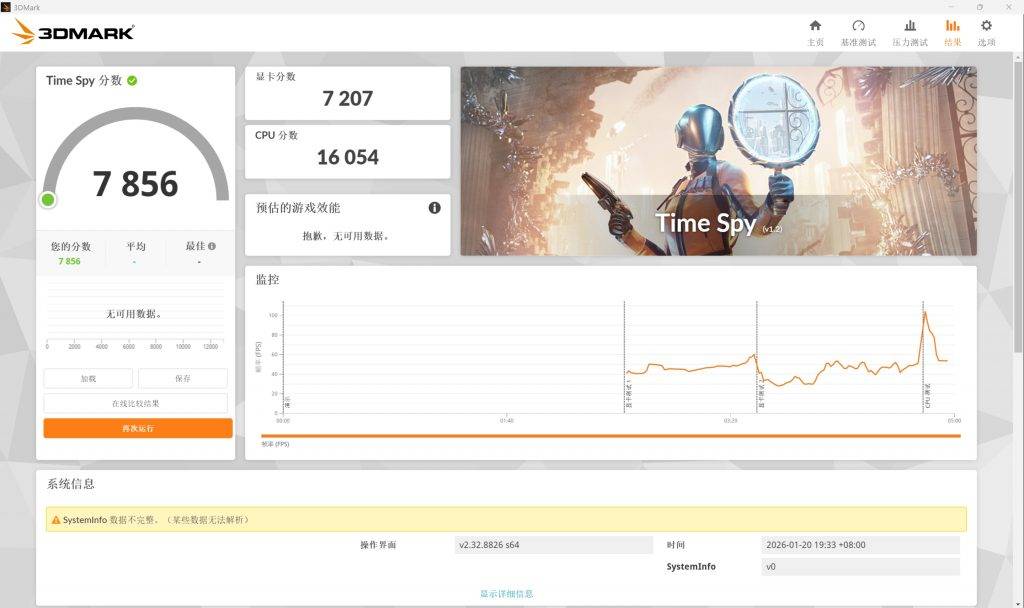
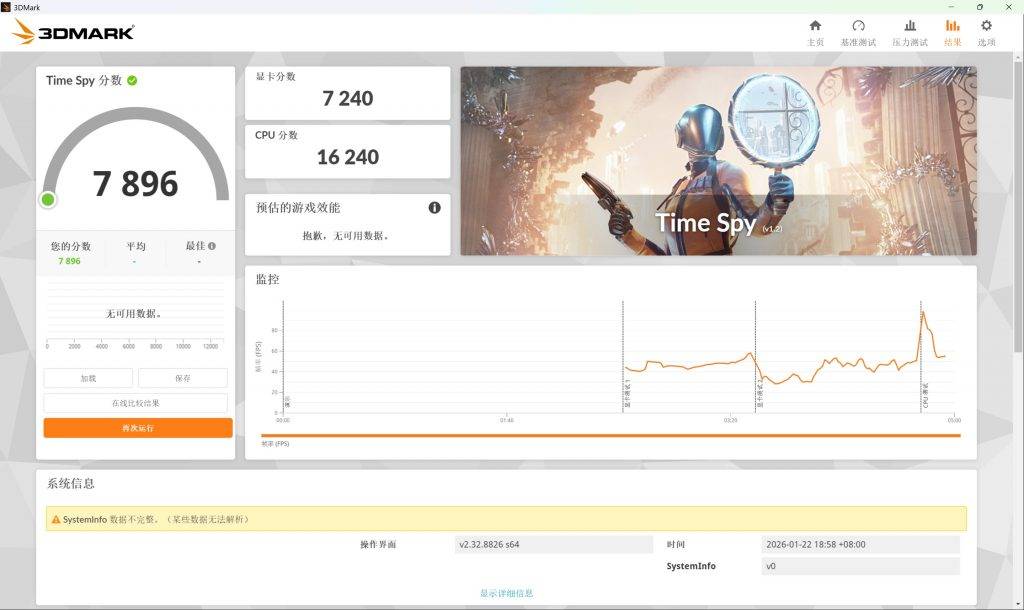
不过,连电和离电的差距在更综合的 PC Mark 10 跑分中进一步体现:10345 比 8673。
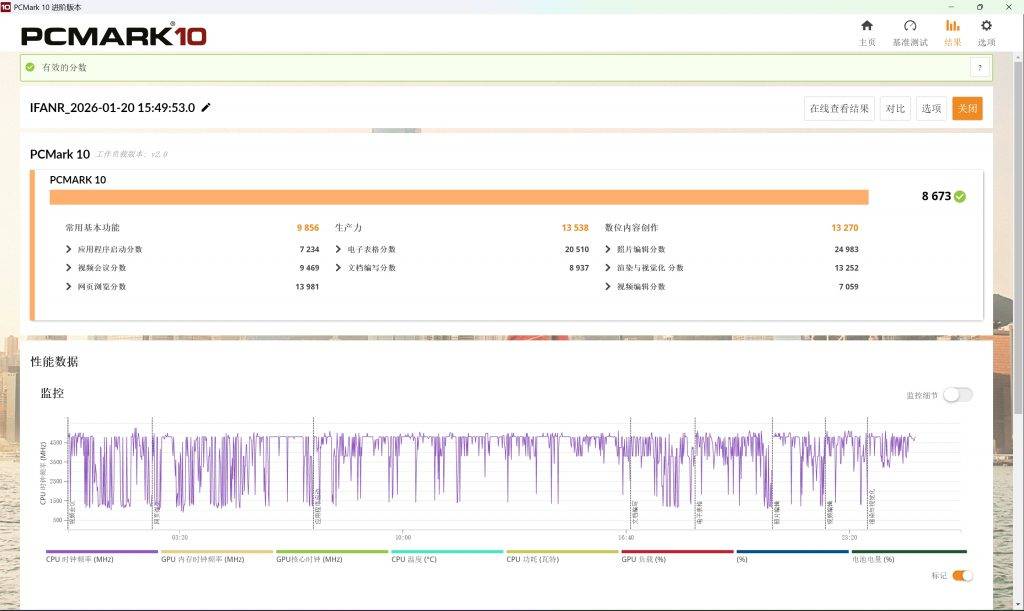
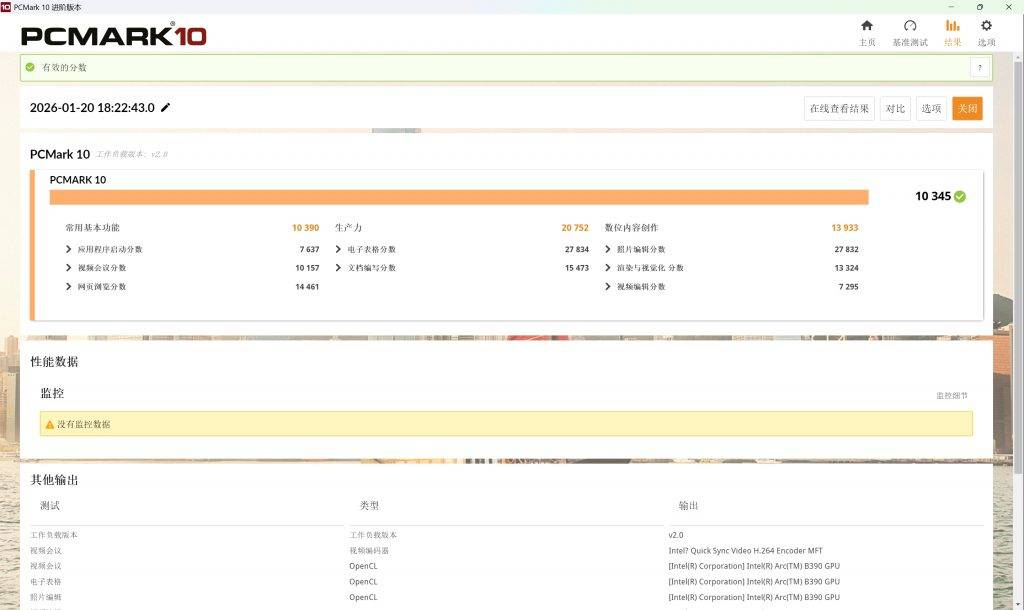
跑分仅供参考,游戏的实际体验更能直观体现性能的进步。这次,我们用这颗新处理器,玩上了最新推出的《明日方舟:终末地》。

目前这款新游戏还不支持第三代酷睿 Ultra 的超分、插帧,中画质和 2.8K 分辨率下,平均帧率有 50fps,即使是多个角色打 Boss 的大场景,游戏也能够流畅清晰地运行。
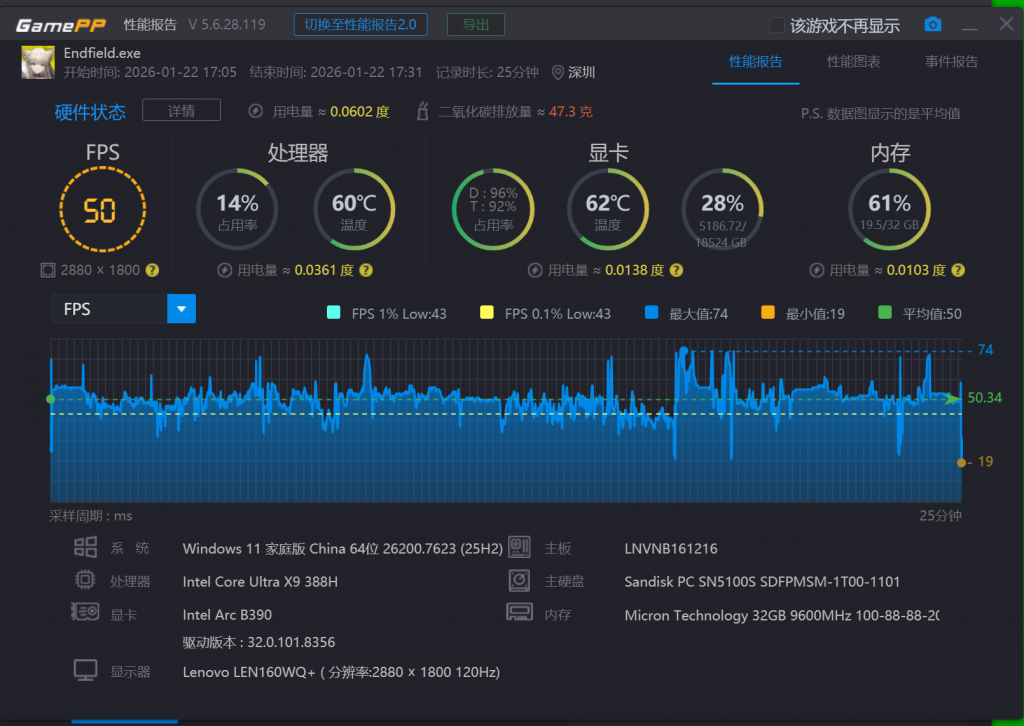
这两年,《黑神话:悟空》已经成为了显卡性能的质检器之一。中画质不开光追,1080P 分辨率,打开 XeSS 帧生成,半小时平均帧率能稳定到 90fps;关闭 XeSS 后,原生帧率在 50 左右浮动。

不过酷睿 Ultra 处理器系列支持 XeSS 多帧生成技术,实现处理器的「越级」表现。
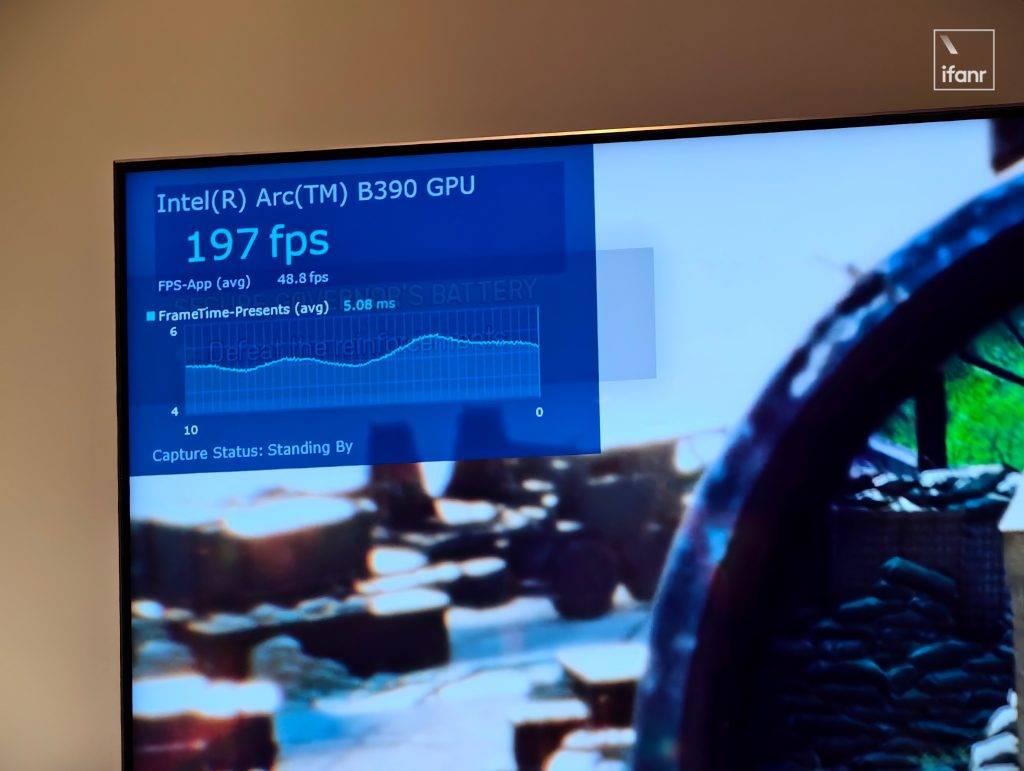
更重要的是,第三代酷睿 Ultra 处理器的出厂就支持多款游戏的 XeSS 3 帧生成技术,能够为每 1 帧生成 3 帧补偿画面,《黑神话》就是其中之一。打开相关选项后,平均帧率会来到 90fps,明显能感觉到更流畅,并且画面也不太能看出进行过帧生成处理。
我们还尝试打开了光追,最低效果下能跑出 55fps,不过画面效果增益不明显,输入延迟也变高了。
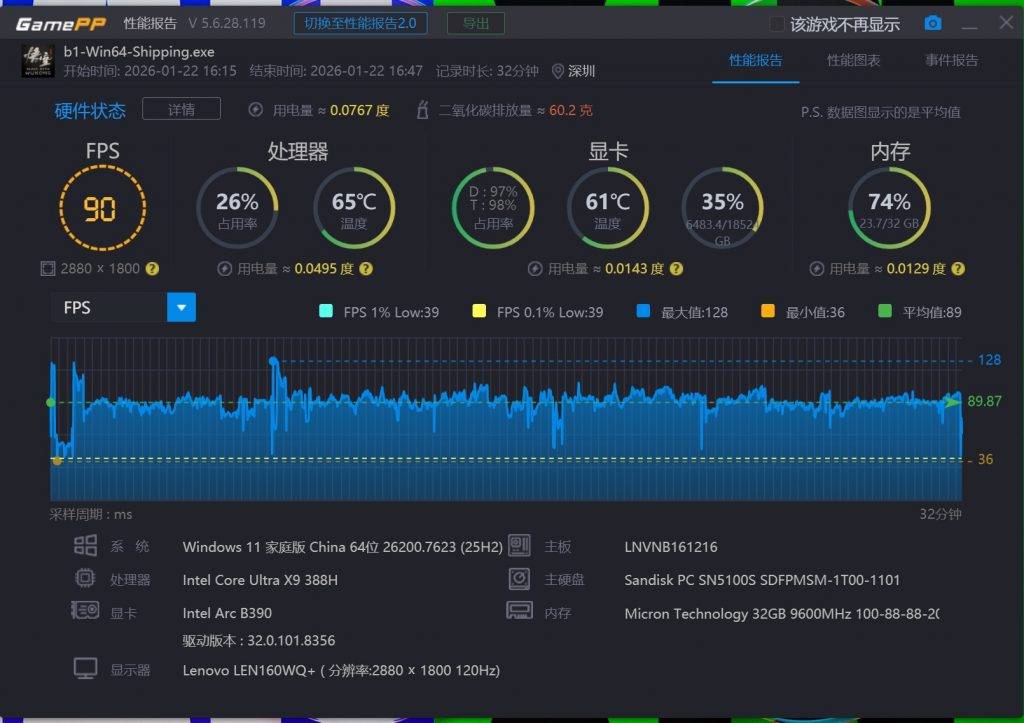
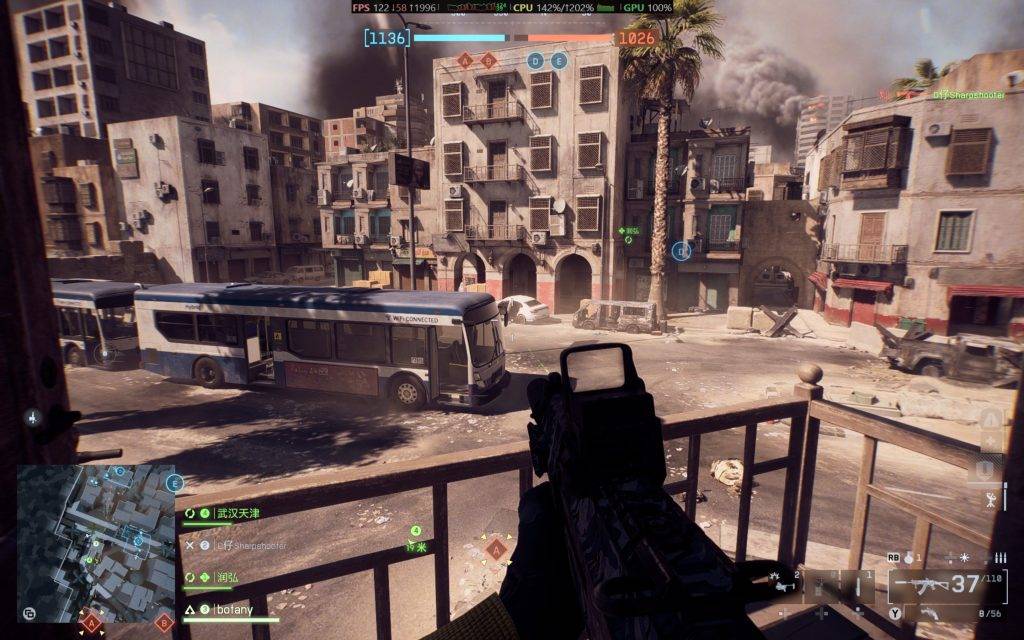
在 CES 上已经有过惊艳表现的《战地风云 6》,我们也测试了一番:在 1080P 分辨率、高画质和开启插帧的条件下,帧率总体在 120fps 左右。或许英特尔和《战地 6》有相关合作,这个游戏的 XeSS 插帧效果相当自然,画面也相当饱满。
我们测试的几款游戏中,画面表现最好的当属《极限竞速:地平线 5》,不仅 1080P 高画质下能跑 120fps,还能开中等光追效果,跑车开起来心旷神怡。

总的来说,酷睿 Ultra X9 388H 带给我一种「陌生感」,这还是英特尔的 x86 芯片吗?
休眠开盖唤醒秒进游戏,续航妥妥用一天,插拔电性能始终如一,这些曾经都是 x86 架构处理器难以逾越的鸿沟。
英特尔的招牌一直都是 CPU,核显总被视作「附赠品」;如今 12 核的 Xe3 GPU,已经能和主流英伟达独显掰掰手腕。
本地跑 AI 的真 · AI PC
现在出厂的新电脑,很难不是「AIPC」,开机就有自带 OEM 厂商的 AI 助手,我们手上这台联想小新就预装了一个「天禧智能体」。

「天禧 AI」自带的聊天机器人可以调用 DeepSeek、豆包等主流模型进行问答,支持 AI 对话、写作、翻译、搜索这些常用的 Agent 功能,平时办公、学习用起来都还算顺手。
不过,天禧 AI 也只是将端云一体的 AI 服务集成到系统层之中,没有完全发挥这颗处理器的性能,实际上酷睿 Ultra X9 388H 能做到的远不止于此。
第三代酷睿 Ultra 系列芯片延续了英特尔 XPU 的架构,可以让 CPU、GPU、NPU 相互协调、共享资源,最多 85% 的内存可以调用给显存——我们手上这台 32GB 的联想小新,能够提供 18 GB 的显存,加上 9600MT/s 的内存速度,比一些独显游戏本都要强了。
如此庞大的显存资源,让这台定位中端的轻薄本能够本地部署大语言模型,成为「真 · AIPC」。
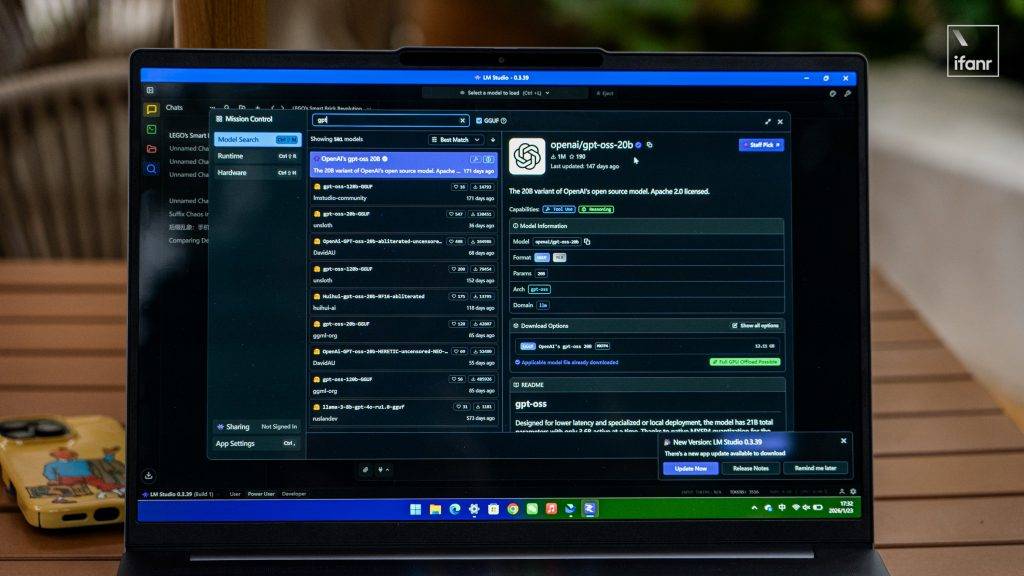
通过 LM Studio,我本地部署了一个 20B 的 GPT-OSS-GGUF 模型,这是去年 8 月 OpenAI 推出的开源模型,量级已经不算太小。
我将一篇 3 千字的稿子抛给它总结一下内容,几乎没有思考几秒,一个详尽的摘要就出现在我面前,速度和在线的 ChatGPT 一样快,内容质量相差不大。
这个模型大小才 6GB,其实压力不算太大,我决定上上强度,部署了一个 20GB 左右的 Qwen3-VL-30B 模型,LM Studio 加载模型的速度明显慢了下来。
用同一篇文章和提示词进行测试,机身也出现了明显发热,不过总体还算保持了一个还算快的生成速度,只是质量对比 GPT-OSS-GGUF 要略逊一筹。
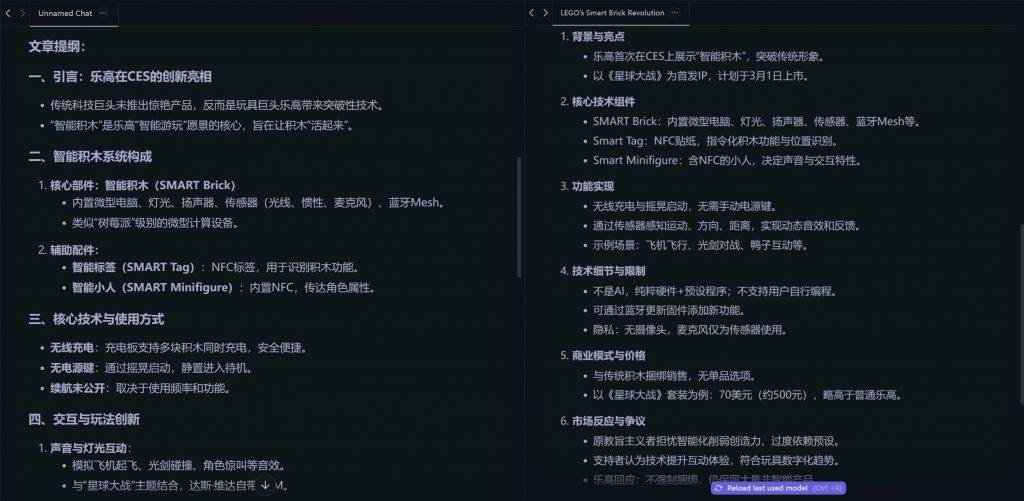
▲ 左:Qwen3-VL-30B;右:GPT-OSS-GGUF-20B
得益于大显存和 GPU 性能,第三代酷睿 Ultra 系列本地跑一个小模型已经不是什么难事,但本地部署平台对英特尔芯片的支持依旧相当有限。
我尝试了目前最好的开源生图平台 Comfy,以及一些本地部署 Stable Diffusion 的方式,都因为这颗英特尔的显卡被拒之门外,连尝试的机会都没有。
如果英特尔真的想做好「本地 AI PC」,那么除了芯片的性能,这也是必须要解决的障碍。
英特尔的「M1 时刻」
在移动领域遭遇苹果、高通、AMD、英伟达多重夹击的英特尔,这几年开始转变思路,不去比拼峰值性能释放,反而选择以退为进,走「能效比」路线,想要创造「轻薄游戏本」这种全新的品类。
经过去年 Ultra 200V、200H 的试水,今年的第三代酷睿 Ultra 系列不仅没让人失望,反而十分让人惊喜,上面的实测数据已经证明,酷睿核显,已经能和英伟达的独显掰手腕了。

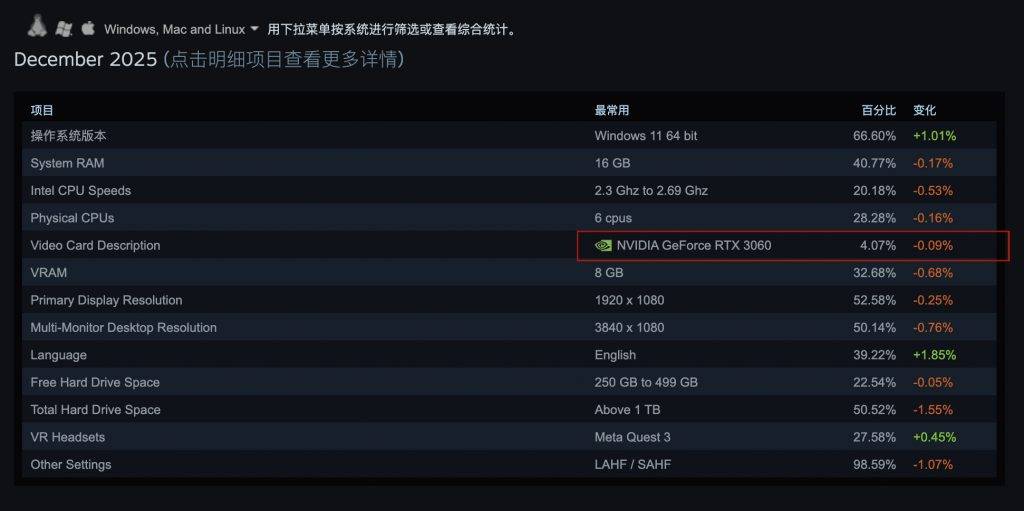
去年 12 月的 Steam 硬件调查显示,RTX 3060 依旧是这个平台上使用率最高的显卡,证明即使这已经是接近 5 岁的产品,依旧是一个足以应对大部分大型游戏的性能标杆。
这也意味着,搭载 Ultra X9 388H 的笔记本,只要 TDP 给够,性能释放也能基本接近一台带有 3060 独显的笔记本,并且更省电、更便携,离电更强。
对于联想小新 Pro16 GT 这种曾经定位比较「中庸」:没轻薄本便携,性能也不比游戏本的产品来说,在第三代酷睿 Ultra 加持下,摇身一变成了性能堪比游戏本,便携性却接近轻薄本的「全能本」。
也就是说,以后不需要塞独立显卡,也不需要狂堆散热,入门游戏本完全可以做成商务本的体积和重量,曾经笔记本「性能」和「便携」的分明泾渭渐渐弥合。
说到底,所谓的游戏本和轻薄本,也是因为处理器能效比一直无法达到理想状态,才不得不做出品类上的区分,而现在,随着芯片制程工艺和架构技术的升级,「既要又要」终于可以实现了。
联想小新只是用第三代酷睿 Ultra 芯片打造的其中一款设备,我更期待像 LG Gram、Dell XPS 这些更极致轻薄的笔记本和这颗处理器能产生什么样的化学反应。

▲ CES 2026 上展出搭载第三代酷睿 Ultra 芯片的戴尔 XPS 笔记本
目前最大的悬念是,这颗用上最新先进制程的酷睿 Ultra 300 系列芯片,成本会不会也水涨船高,导致只能专属于高端笔记本产品。
如果产品价格合理,在显卡价格大涨的今年,买一台酷睿 Ultra 300 系列的轻薄本等于送一个独显,无疑相当具有性价比。
高能效的芯片以前不是没有,但在 x86 阵营,目前第三代酷睿 Ultra 系列确实是性能、能耗、成本上平衡得最出色的移动端产品,甚至还克服了 x86 离开电源性能跳水的通病。
除了常规的 PC 产品,作为高性能、低能耗的移动平台处理器,第三代酷睿 Ultra 的出现,会催生出更多另类的 PC 产品,甚至其中一些已经在今年的 CES 上抢先登场了。
Windows 掌机产品
这几年的 Windows 掌机风头正盛,却苦于缺少一颗足够高效的芯片,难以摆脱大块头、低续航的困境。
随着第三代酷睿 Ultra 芯片的推出,加上微软正在推广的「Xbox 掌机版 Windows 界面」,接下来几年 Win 掌机确实未来可期——当然,搭载第三代酷睿 Ultra 的掌机价格想必不会太低。

双屏/多屏笔记本
今年华硕将推出新的 ROG 幻 16 双屏笔记本(Zephyrus Duo),配备完整的两个 16 寸大屏。

双屏无疑是对性能和续航的双重考验,以往这样的产品更多只停留在探索性质;而高性能、低能耗的第三代酷睿 Ultra,无疑非常适合这种设备——ROG 幻 16 双屏笔记本,作为一台双屏游戏本,厚度和重量都控制得比较出色。
不只「双屏」,未来的折叠屏、卷轴屏等「大屏笔记本」,都能因为这种低能耗高性能处理器,得以进一步走向大众市场。
迷你 PC
当一颗芯片同时实现高性能、低发热、强图形,还能做成什么样的产品?苹果已经用 Mac mini 产品给出了答案。

在 CES 上,我们也看到了一些迷你 PC 样机,体型比一个饭盒还小,却同样能提供接近 RTX 3060 独显的图形性能。
馋 Mac mini 身子,却离不开 Windows 和 x86 的消费者,终于有了一个最佳选择。
个人 AI PC
作为英特尔在 AIPC 时代推出的全新处理器系列,Ultra 系列一直以来的亮点就是对 AI 的支持。
如果说 Ultra 100 还是只能用 NPU 加速一些聊胜于无的 Windows 本地 AI 功能,那第三代酷睿 Ultra 就真正的将本地部署轻量级模型的能力,带到了个人笔记本上。
不止英特尔,AMD、苹果都在做这种能将内存转换为显存的处理器,未来越来越多个人电脑,能够成为本地能跑模型的「AIPC」。
一年前的「Lunar Lake」酷睿 Ultra 200V 系列,第一次证明了 x86 芯片也能实现高能效,但它的上限不算太高,芯片架构也由于成本问题没能延续,更多只是英特尔的一次探索。
而这颗「Panther Lake」第三代酷睿 Ultra 芯片,一下子让我回到六年前,体验到苹果 M1 的那个感觉——那么小那么轻的设备,性能却能堪比那些庞然大物。
不止是 PC 产品性能和能效一次飞跃,也预示着更多可能性的发生。
#欢迎关注爱范儿官方微信公众号:爱范儿(微信号:ifanr),更多精彩内容第一时间为您奉上。
爱范儿 |
原文链接 ·
查看评论 ·
新浪微博