解题思路

首先谈谈三阶幻方，固然是可以通过定义去判断，但写起来很麻烦，效率也不高。实际上，三阶幻方的解是固定的，有以下八种。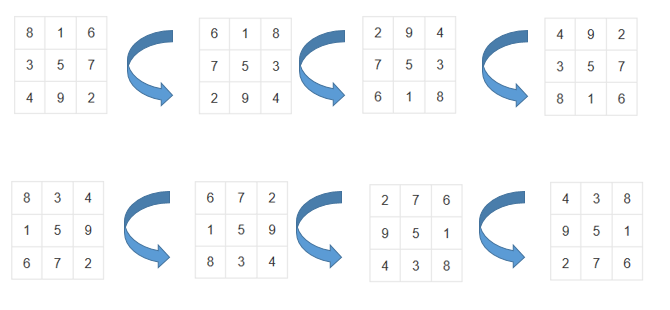

自然是不可能逐个判断是不是这八个之一，大家仔细观察，相信很容易找出这八个解的共同点，首先中间的元素都是五，角上元素都是偶数，中点都是奇数。同一行的解可以通过旋转得到，第一行镜像，可以得到第二行。也就是说，三阶幻方本质只有一种解，其余都是旋转镜像的体现。
我们可以依据这一点，写出优雅简洁的代码。

1. 遍历中间的部分，只有是五的时候，才判断以他为中心的三阶方阵是否是幻方。
2. 五已经比对过了，只需要比对其他八个元素，由于解的旋转不变特性，这里将八个元素按顺序存放，方便后面比较，顺序如下图。
3. 解的编码，如何表示旋转镜像，参考旋转数组这题的思想，将前面部分的放在后面就达到了旋转的效果。镜像只需要反向迭代就好了。
   
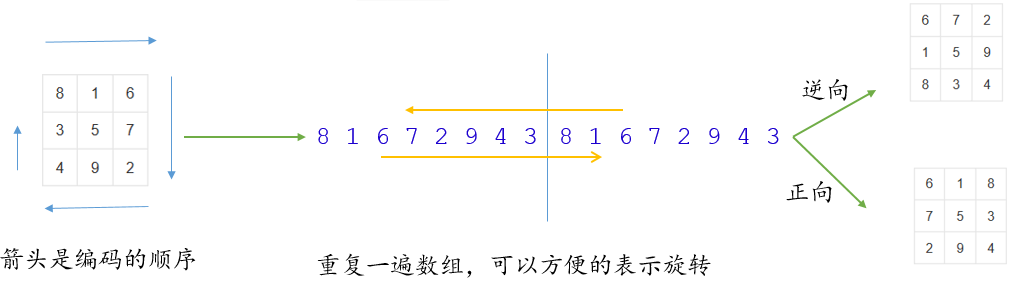
   4.第二步输入的数组首位元素和8 6 2 4逐个比较决定可能的解，从编码的数组中取出正向镜像两个解比较是否其一，就可确定是否是幻方。

代码

###cpp

class Solution {
public:
    vector<int> m={8,1,6,7,2,9,4,3,8,1,6,7,2,9,4,3};
    int numMagicSquaresInside(vector<vector<int>>& grid) {
        int di[8]={-1,-1,-1,0,1,1,1,0};
        int dj[8]={-1,0,1,1,1,0,-1,-1};
        int count=0;
        for(int i=1;i<grid.size()-1;i++)
            for(int j=1;j<grid[0].size()-1;j++)
                if(grid[i][j]==5){
                    vector<int> around;
                    for(int k=0;k<8;k++)
                        around.push_back(grid[i+di[k]][j+dj[k]]);
                    count+=IsMagic(around);
                }
        return count;
    }
    bool IsMagic(vector<int>& v){
        for(int i=0;i<8;i+=2)
            if(m[i]==v[0])
            return v==vector<int>(m.begin()+i,m.begin()+i+8)
            ||v==vector<int>(m.rbegin()+7-i,m.rbegin()+15-i);
        return false;//奇数元素
    }
};