阅读视图
银行加速创新押品融资,“商业秘密”贷款不再是秘密
加州拟推电动汽车购车补贴,特斯拉将被排除在外
美联储卡什卡利:在12月降息是合理的考虑
德意志银行预计欧元兑美元将在2025年跌至平价
大运集团回应旗下公司重整事宜:仅重整新能源板块
蒂森克虏伯钢铁子公司计划削减1.1万工作岗位
Natixis Investment Managers据悉与忠利集团就潜在合作进行谈判
SpaceX第七次试飞计划最早明年1月11日进行
印尼称苹果1亿美元投资计划不足以解除禁令
美股三大指数集体收涨,大型科技股多数走强
遍历计数,C 0ms
Problem: 100336. 交替组 I
[TOC]
思路
直接按题意遍历计数。
Code
执行用时分布0ms击败100.00%;消耗内存分布5.69MB击败100.00%
###C
int numberOfAlternatingGroups(int* colors, int colorsSize) {
int ans = (colors[colorsSize - 2] != colors[colorsSize - 1] && colors[colorsSize - 1] != colors[0])
+ (colors[colorsSize - 1] != colors[0] && colors[0] != colors[1]);
for (int i = 2; i < colorsSize; ++ i)
if ((colors[i - 2] != colors[i - 1] && colors[i - 1] != colors[i])) ++ ans;
return ans;
}
###Python3
class Solution:
def numberOfAlternatingGroups(self, colors: List[int]) -> int:
n, colors = len(colors), colors + colors[:2]
return sum(colors[i] != colors[i + 1] != colors[i + 2] for i in range(n))
您若还有不同方法,欢迎贴在评论区,一起交流探讨! ^_^
↓ 点个赞,点收藏,留个言,再划走,感谢您支持作者! ^_^
每日一题-交替组 I🟢
给你一个整数数组 colors ,它表示一个由红色和蓝色瓷砖组成的环,第 i 块瓷砖的颜色为 colors[i] :
-
colors[i] == 0表示第i块瓷砖的颜色是 红色 。 -
colors[i] == 1表示第i块瓷砖的颜色是 蓝色 。
环中连续 3 块瓷砖的颜色如果是 交替 颜色(也就是说中间瓷砖的颜色与它 左边 和 右边 的颜色都不同),那么它被称为一个 交替 组。
请你返回 交替 组的数目。
注意 ,由于 colors 表示一个 环 ,第一块 瓷砖和 最后一块 瓷砖是相邻的。
示例 1:
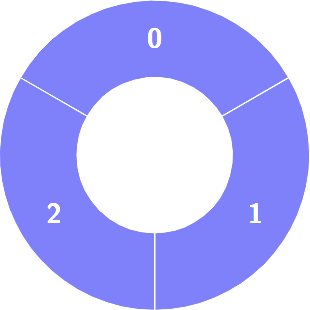
输入:colors = [1,1,1]
输出:0
解释:
示例 2:
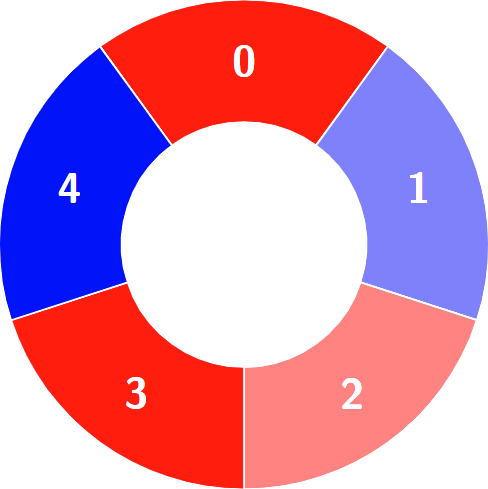
输入:colors = [0,1,0,0,1]
输出:3
解释:
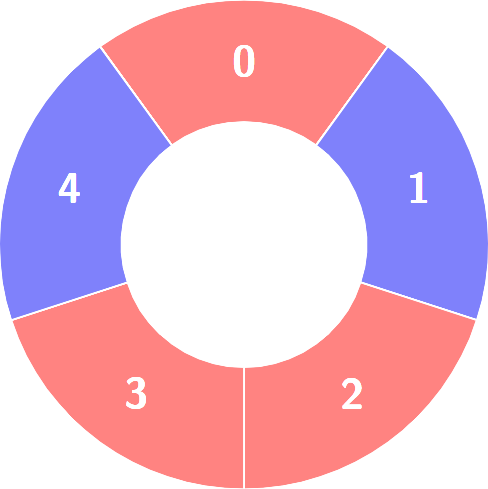
交替组包括:
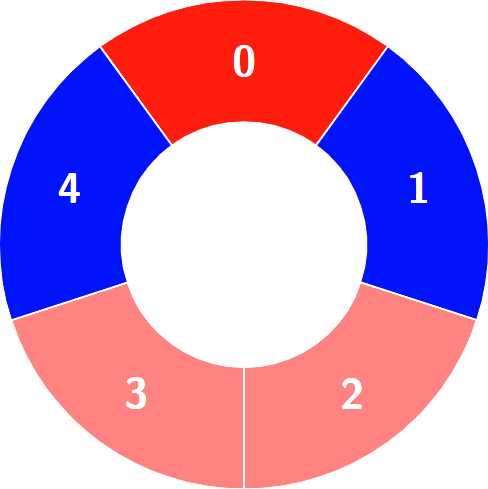
提示:
3 <= colors.length <= 1000 <= colors[i] <= 1
JavaScript 中的 `concat()` 方法详解
交替组 I
方法一:模拟
思路
按照题意遍历数组 $\textit{colors}$ 的每个元素,判断其前一个元素和后一个元素是否都与当前元素不同,如果满足,则将结果加 $1$。注意瓷砖是环形的,则数组的首尾元素是相邻的。最后返回结果。
代码
###Python
class Solution:
def numberOfAlternatingGroups(self, colors: List[int]) -> int:
n = len(colors)
res = 0
for i in range(n):
if colors[i] != colors[i - 1] and colors[i] != colors[(i + 1) % n]:
res += 1
return res
###Java
class Solution {
public int numberOfAlternatingGroups(int[] colors) {
int n = colors.length;
int res = 0;
for (int i = 0; i < n; i++) {
if (colors[i] != colors[(i - 1 + n) % n] && colors[i] != colors[(i + 1) % n]) {
res += 1;
}
}
return res;
}
}
###C#
public class Solution {
public int NumberOfAlternatingGroups(int[] colors) {
int n = colors.Length;
int res = 0;
for (int i = 0; i < n; i++) {
if (colors[i] != colors[(i - 1 + n) % n] && colors[i] != colors[(i + 1) % n]) {
res += 1;
}
}
return res;
}
}
###C++
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors) {
int n = colors.size();
int res = 0;
for (int i = 0; i < n; i++) {
if (colors[i] != colors[(i - 1 + n) % n] && colors[i] != colors[(i + 1) % n]) {
res += 1;
}
}
return res;
}
};
###Go
func numberOfAlternatingGroups(colors []int) int {
n := len(colors)
res := 0
for i := 0; i < n; i++ {
if colors[i] != colors[(i-1+n)%n] && colors[i] != colors[(i+1)%n] {
res++
}
}
return res
}
###C
int numberOfAlternatingGroups(int* colors, int colorsSize) {
int res = 0;
for (size_t i = 0; i < colorsSize; i++) {
if (colors[i] != colors[(i - 1 + colorsSize) % colorsSize] && colors[i] != colors[(i + 1) % colorsSize]) {
res += 1;
}
}
return res;
}
###JavaScript
var numberOfAlternatingGroups = function(colors) {
const n = colors.length;
let res = 0;
for (let i = 0; i < n; i++) {
if (colors[i] !== colors[(i - 1 + n) % n] && colors[i] !== colors[(i + 1) % n]) {
res++;
}
}
return res;
};
###TypeScript
function numberOfAlternatingGroups(colors: number[]): number {
const n = colors.length;
let res = 0;
for (let i = 0; i < n; i++) {
if (colors[i] !== colors[(i - 1 + n) % n] && colors[i] !== colors[(i + 1) % n]) {
res++;
}
}
return res;
};
###Rust
impl Solution {
pub fn number_of_alternating_groups(colors: Vec<i32>) -> i32 {
let n = colors.len();
let mut res = 0;
for i in 0..n {
if colors[i] != colors[(i + n - 1) % n] && colors[i] != colors[(i + 1) % n] {
res += 1;
}
}
res
}
}
复杂度分析
-
时间复杂度:$O(n)$。
-
空间复杂度:$O(1)$。
O(n) 做法(Python/Java/C++/C/Go/JS/Rust)
本题和 3208. 交替组 II 是一样的,令 $k=3$ 即可,请看 我的题解。
滑动窗口
解法:滑动窗口
枚举组的开头,那么组中间的 $(k - 2)$ 个元素都需要满足“与两边的颜色不同”的条件。预处理哪些元素和两边的颜色不同,再用滑动窗口统计中间的 $(k - 2)$ 个元素中,有几个满足该条件即可。复杂度 $\mathcal{O}(n)$。
参考代码(c++)
###cpp
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int K) {
int n = colors.size();
// 预处理哪些元素与两边颜色不同
int f[n];
for (int i = 0; i < n; i++) {
int x = colors[(i - 1 + n) % n];
int y = colors[i];
int z = colors[(i + 1) % n];
if (x != y && y != z) f[i] = 1;
else f[i] = 0;
}
// 滑动窗口
int sm = 0;
for (int i = 1; i + 1 < K; i++) sm += f[i];
int ans = 0;
for (int i = 0; i < n; i++) {
if (sm == K - 2) ans++;
sm -= f[(i + 1) % n];
sm += f[(i + K - 1) % n];
}
return ans;
}
};