[Python3/Java/C++/Go/TypeScript] 一题一解:扫描线(清晰题解)
方法一:扫描线
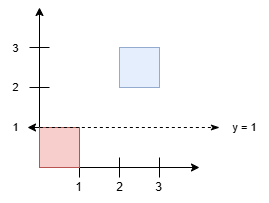
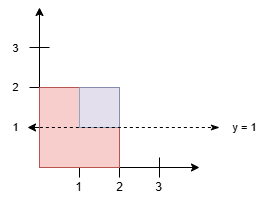
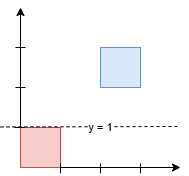
本题可以使用扫描线算法来计算所有正方形的总面积。
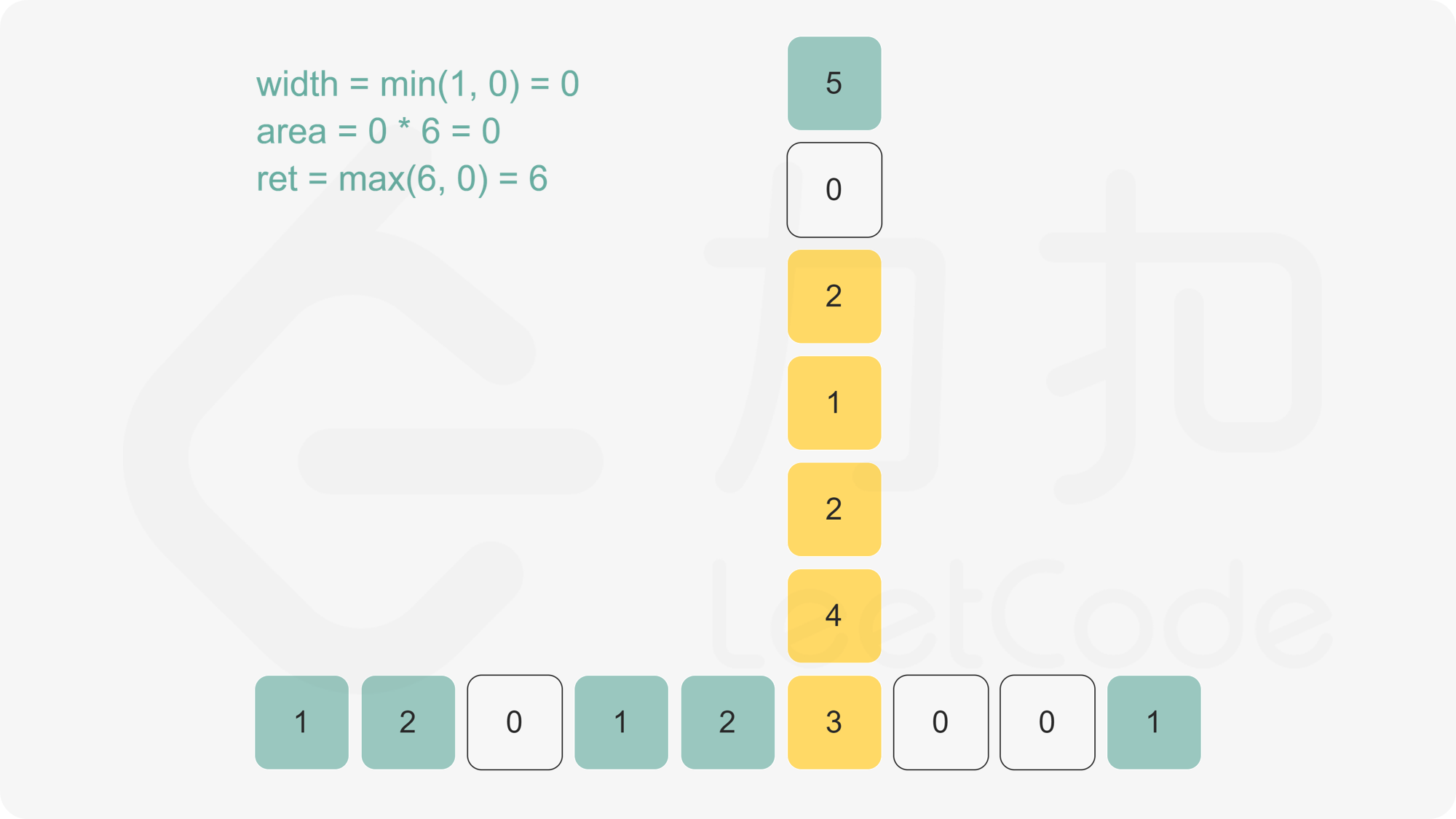
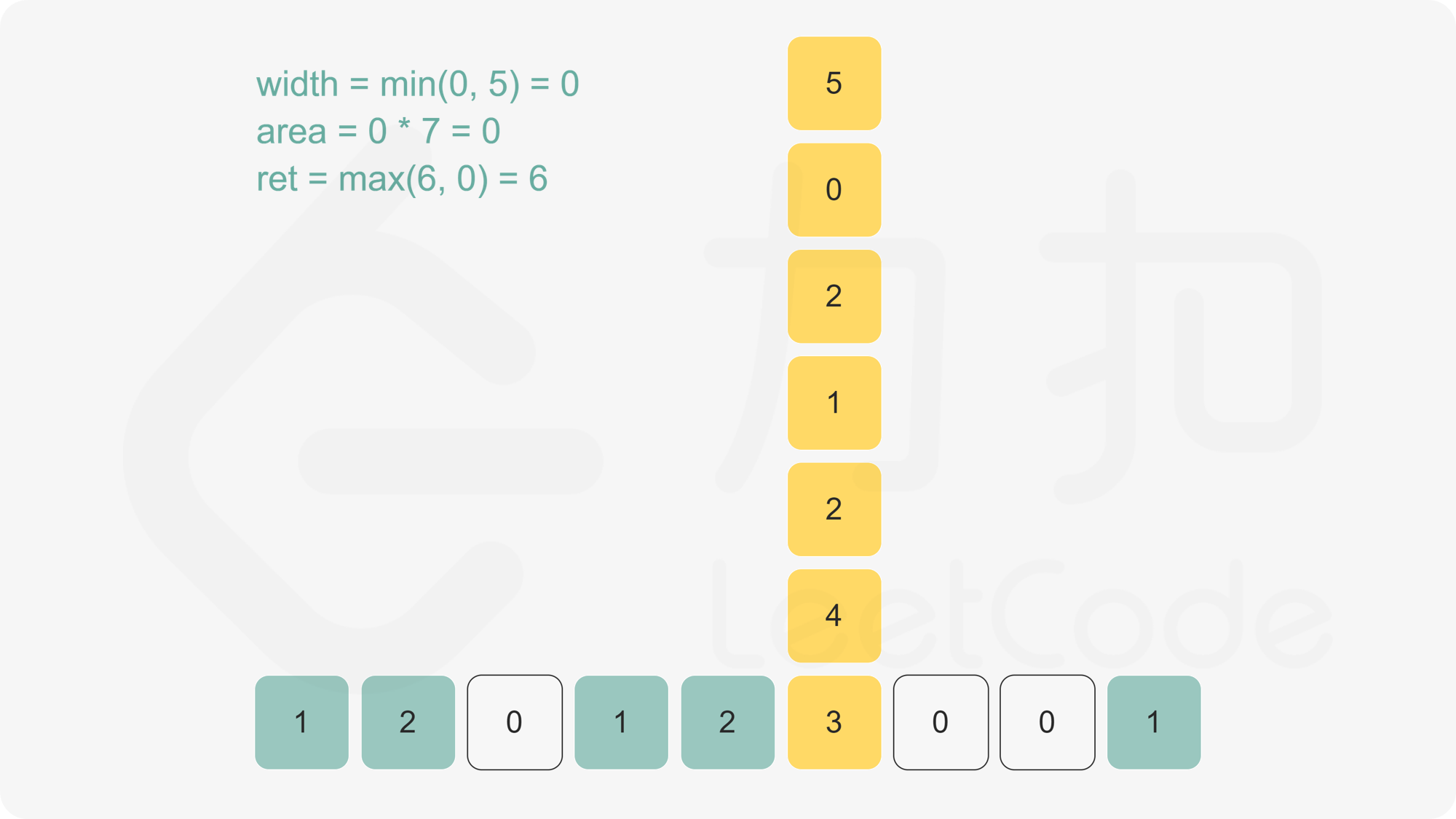
我们将每个正方形的上下边界作为扫描线的事件点,按 $y$ 坐标从小到大排序。对于每个事件点,我们使用线段树来维护当前扫描线下方被覆盖的 $x$ 轴区间长度,从而计算出当前扫描线与上一个扫描线之间的面积增量。
具体步骤如下:
- 预处理事件点:对于每个正方形,计算其上下边界的 $y$ 坐标,并将其作为事件点加入事件列表中。每个事件点包含 $y$ 坐标、左边界 $x_1$、右边界 $x_2$ 以及一个标志(表示是上边界还是下边界)。
- 排序事件点:将所有事件点按 $y$ 坐标从小到大排序。
- 构建线段树:使用离散化后的 $x$ 坐标构建线段树,用于维护当前被覆盖的 $x$ 轴区间长度。
-
扫描事件点:遍历排序后的事件点列表,对于每个事件点:
- 计算当前事件点与上一个事件点之间的面积增量,并累加到总面积中。
- 根据当前事件点的类型(上边界或下边界),更新线段树,增加或减少对应的 $x$ 轴区间覆盖计数。
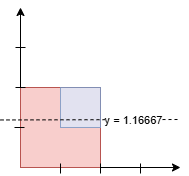
- 计算目标面积:总面积的一半即为目标面积。
- 再次扫描事件点:再次遍历事件点列表,计算累计面积,当累计面积达到目标面积时,计算并返回对应的 $y$ 坐标。
###python
class Node:
__slots__ = ("l", "r", "cnt", "length")
def __init__(self):
self.l = self.r = 0
self.cnt = self.length = 0
class SegmentTree:
def __init__(self, nums):
n = len(nums) - 1
self.nums = nums
self.tr = [Node() for _ in range(n << 2)]
self.build(1, 0, n - 1)
def build(self, u, l, r):
self.tr[u].l, self.tr[u].r = l, r
if l != r:
mid = (l + r) >> 1
self.build(u << 1, l, mid)
self.build(u << 1 | 1, mid + 1, r)
def modify(self, u, l, r, k):
if self.tr[u].l >= l and self.tr[u].r <= r:
self.tr[u].cnt += k
else:
mid = (self.tr[u].l + self.tr[u].r) >> 1
if l <= mid:
self.modify(u << 1, l, r, k)
if r > mid:
self.modify(u << 1 | 1, l, r, k)
self.pushup(u)
def pushup(self, u):
if self.tr[u].cnt:
self.tr[u].length = self.nums[self.tr[u].r + 1] - self.nums[self.tr[u].l]
elif self.tr[u].l == self.tr[u].r:
self.tr[u].length = 0
else:
self.tr[u].length = self.tr[u << 1].length + self.tr[u << 1 | 1].length
@property
def length(self):
return self.tr[1].length
class Solution:
def separateSquares(self, squares: List[List[int]]) -> float:
xs = set()
segs = []
for x1, y1, l in squares:
x2, y2 = x1 + l, y1 + l
xs.update([x1, x2])
segs.append((y1, x1, x2, 1))
segs.append((y2, x1, x2, -1))
segs.sort()
st = sorted(xs)
tree = SegmentTree(st)
d = {x: i for i, x in enumerate(st)}
area = 0
y0 = 0
for y, x1, x2, k in segs:
area += (y - y0) * tree.length
tree.modify(1, d[x1], d[x2] - 1, k)
y0 = y
target = area / 2
area = 0
y0 = 0
for y, x1, x2, k in segs:
t = (y - y0) * tree.length
if area + t >= target:
return y0 + (target - area) / tree.length
area += t
tree.modify(1, d[x1], d[x2] - 1, k)
y0 = y
return 0
###java
class Node {
int l, r, cnt, length;
}
class SegmentTree {
private Node[] tr;
private int[] nums;
public SegmentTree(int[] nums) {
this.nums = nums;
int n = nums.length - 1;
tr = new Node[n << 2];
for (int i = 0; i < tr.length; ++i) {
tr[i] = new Node();
}
build(1, 0, n - 1);
}
private void build(int u, int l, int r) {
tr[u].l = l;
tr[u].r = r;
if (l != r) {
int mid = (l + r) >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
}
}
public void modify(int u, int l, int r, int k) {
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].cnt += k;
} else {
int mid = (tr[u].l + tr[u].r) >> 1;
if (l <= mid) {
modify(u << 1, l, r, k);
}
if (r > mid) {
modify(u << 1 | 1, l, r, k);
}
}
pushup(u);
}
private void pushup(int u) {
if (tr[u].cnt > 0) {
tr[u].length = nums[tr[u].r + 1] - nums[tr[u].l];
} else if (tr[u].l == tr[u].r) {
tr[u].length = 0;
} else {
tr[u].length = tr[u << 1].length + tr[u << 1 | 1].length;
}
}
public int query() {
return tr[1].length;
}
}
class Solution {
public double separateSquares(int[][] squares) {
Set<Integer> xs = new HashSet<>();
List<int[]> segs = new ArrayList<>();
for (int[] sq : squares) {
int x1 = sq[0], y1 = sq[1], l = sq[2];
int x2 = x1 + l, y2 = y1 + l;
xs.add(x1);
xs.add(x2);
segs.add(new int[] {y1, x1, x2, 1});
segs.add(new int[] {y2, x1, x2, -1});
}
segs.sort(Comparator.comparingInt(a -> a[0]));
int[] st = new int[xs.size()];
int i = 0;
for (int x : xs) {
st[i++] = x;
}
Arrays.sort(st);
SegmentTree tree = new SegmentTree(st);
Map<Integer, Integer> d = new HashMap<>(st.length);
for (i = 0; i < st.length; i++) {
d.put(st[i], i);
}
double area = 0.0;
int y0 = 0;
for (int[] s : segs) {
int y = s[0], x1 = s[1], x2 = s[2], k = s[3];
area += (double) (y - y0) * tree.query();
tree.modify(1, d.get(x1), d.get(x2) - 1, k);
y0 = y;
}
double target = area / 2.0;
area = 0.0;
y0 = 0;
for (int[] s : segs) {
int y = s[0], x1 = s[1], x2 = s[2], k = s[3];
double t = (double) (y - y0) * tree.query();
if (area + t >= target) {
return y0 + (target - area) / tree.query();
}
area += t;
tree.modify(1, d.get(x1), d.get(x2) - 1, k);
y0 = y;
}
return 0.0;
}
}
###cpp
struct Node {
int l = 0, r = 0, cnt = 0;
int length = 0;
};
class SegmentTree {
private:
vector<Node> tr;
vector<int> nums;
void build(int u, int l, int r) {
tr[u].l = l;
tr[u].r = r;
if (l != r) {
int mid = (l + r) >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
}
}
void pushup(int u) {
if (tr[u].cnt > 0) {
tr[u].length = nums[tr[u].r + 1] - nums[tr[u].l];
} else if (tr[u].l == tr[u].r) {
tr[u].length = 0;
} else {
tr[u].length = tr[u << 1].length + tr[u << 1 | 1].length;
}
}
public:
SegmentTree(const vector<int>& nums)
: nums(nums) {
int n = (int) nums.size() - 1;
tr.assign(n << 2, Node());
build(1, 0, n - 1);
}
void modify(int u, int l, int r, int k) {
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].cnt += k;
} else {
int mid = (tr[u].l + tr[u].r) >> 1;
if (l <= mid) modify(u << 1, l, r, k);
if (r > mid) modify(u << 1 | 1, l, r, k);
}
pushup(u);
}
int query() const {
return tr[1].length;
}
};
class Solution {
public:
double separateSquares(vector<vector<int>>& squares) {
set<int> xs;
vector<array<int, 4>> segs;
for (auto& sq : squares) {
int x1 = sq[0], y1 = sq[1], l = sq[2];
int x2 = x1 + l, y2 = y1 + l;
xs.insert(x1);
xs.insert(x2);
segs.push_back({y1, x1, x2, 1});
segs.push_back({y2, x1, x2, -1});
}
sort(segs.begin(), segs.end(), [](const auto& a, const auto& b) {
return a[0] < b[0];
});
vector<int> st;
st.reserve(xs.size());
for (int x : xs) st.push_back(x);
SegmentTree tree(st);
unordered_map<int, int> d;
d.reserve(st.size() * 2);
for (int i = 0; i < (int) st.size(); i++) d[st[i]] = i;
double area = 0.0;
int y0 = 0;
for (auto& s : segs) {
int y = s[0], x1 = s[1], x2 = s[2], k = s[3];
area += (double) (y - y0) * tree.query();
tree.modify(1, d[x1], d[x2] - 1, k);
y0 = y;
}
double target = area / 2.0;
area = 0.0;
y0 = 0;
for (auto& s : segs) {
int y = s[0], x1 = s[1], x2 = s[2], k = s[3];
double t = (double) (y - y0) * tree.query();
if (area + t >= target) {
return y0 + (target - area) / tree.query();
}
area += t;
tree.modify(1, d[x1], d[x2] - 1, k);
y0 = y;
}
return 0.0;
}
};
###go
type Node struct {
l, r int
cnt int
length int
}
type SegmentTree struct {
tr []Node
nums []int
}
func NewSegmentTree(nums []int) *SegmentTree {
n := len(nums) - 1
tr := make([]Node, n<<2)
t := &SegmentTree{tr: tr, nums: nums}
t.build(1, 0, n-1)
return t
}
func (t *SegmentTree) build(u, l, r int) {
t.tr[u].l = l
t.tr[u].r = r
if l != r {
mid := (l + r) >> 1
t.build(u<<1, l, mid)
t.build(u<<1|1, mid+1, r)
}
}
func (t *SegmentTree) modify(u, l, r, k int) {
if l > r {
return
}
if t.tr[u].l >= l && t.tr[u].r <= r {
t.tr[u].cnt += k
} else {
mid := (t.tr[u].l + t.tr[u].r) >> 1
if l <= mid {
t.modify(u<<1, l, r, k)
}
if r > mid {
t.modify(u<<1|1, l, r, k)
}
}
t.pushup(u)
}
func (t *SegmentTree) pushup(u int) {
if t.tr[u].cnt > 0 {
t.tr[u].length = t.nums[t.tr[u].r+1] - t.nums[t.tr[u].l]
} else if t.tr[u].l == t.tr[u].r {
t.tr[u].length = 0
} else {
t.tr[u].length = t.tr[u<<1].length + t.tr[u<<1|1].length
}
}
func (t *SegmentTree) query() int {
return t.tr[1].length
}
func separateSquares(squares [][]int) float64 {
pos := make(map[int]bool)
xs := make([]int, 0)
segs := make([][]int, 0, len(squares)*2)
for _, sq := range squares {
x1, y1, l := sq[0], sq[1], sq[2]
x2, y2 := x1+l, y1+l
if !pos[x1] {
pos[x1] = true
xs = append(xs, x1)
}
if !pos[x2] {
pos[x2] = true
xs = append(xs, x2)
}
segs = append(segs, []int{y1, x1, x2, 1})
segs = append(segs, []int{y2, x1, x2, -1})
}
sort.Slice(segs, func(i, j int) bool { return segs[i][0] < segs[j][0] })
sort.Ints(xs)
tree := NewSegmentTree(xs)
d := make(map[int]int, len(xs))
for i, x := range xs {
d[x] = i
}
area := 0.0
y0 := 0
for _, s := range segs {
y, x1, x2, k := s[0], s[1], s[2], s[3]
area += float64(y-y0) * float64(tree.query())
tree.modify(1, d[x1], d[x2]-1, k)
y0 = y
}
target := area / 2.0
area = 0.0
y0 = 0
for _, s := range segs {
y, x1, x2, k := s[0], s[1], s[2], s[3]
curLen := tree.query()
t := float64(y-y0) * float64(curLen)
if area+t >= target {
return float64(y0) + (target-area)/float64(curLen)
}
area += t
tree.modify(1, d[x1], d[x2]-1, k)
y0 = y
}
return 0.0
}
###ts
class Node {
l = 0;
r = 0;
cnt = 0;
length = 0;
}
class SegmentTree {
private tr: Node[];
private nums: number[];
constructor(nums: number[]) {
this.nums = nums;
const n = nums.length - 1;
this.tr = Array.from({ length: n << 2 }, () => new Node());
this.build(1, 0, n - 1);
}
private build(u: number, l: number, r: number): void {
this.tr[u].l = l;
this.tr[u].r = r;
if (l !== r) {
const mid = (l + r) >> 1;
this.build(u << 1, l, mid);
this.build((u << 1) | 1, mid + 1, r);
}
}
modify(u: number, l: number, r: number, k: number): void {
if (l > r) return;
if (this.tr[u].l >= l && this.tr[u].r <= r) {
this.tr[u].cnt += k;
} else {
const mid = (this.tr[u].l + this.tr[u].r) >> 1;
if (l <= mid) this.modify(u << 1, l, r, k);
if (r > mid) this.modify((u << 1) | 1, l, r, k);
}
this.pushup(u);
}
private pushup(u: number): void {
if (this.tr[u].cnt > 0) {
this.tr[u].length = this.nums[this.tr[u].r + 1] - this.nums[this.tr[u].l];
} else if (this.tr[u].l === this.tr[u].r) {
this.tr[u].length = 0;
} else {
this.tr[u].length = this.tr[u << 1].length + this.tr[(u << 1) | 1].length;
}
}
query(): number {
return this.tr[1].length;
}
}
function separateSquares(squares: number[][]): number {
const xsSet = new Set<number>();
const segs: number[][] = [];
for (const [x1, y1, l] of squares) {
const [x2, y2] = [x1 + l, y1 + l];
xsSet.add(x1);
xsSet.add(x2);
segs.push([y1, x1, x2, 1]);
segs.push([y2, x1, x2, -1]);
}
segs.sort((a, b) => a[0] - b[0]);
const xs = Array.from(xsSet);
xs.sort((a, b) => a - b);
const tree = new SegmentTree(xs);
const d = new Map<number, number>();
for (let i = 0; i < xs.length; i++) {
d.set(xs[i], i);
}
let area = 0.0;
let y0 = 0;
for (const [y, x1, x2, k] of segs) {
area += (y - y0) * tree.query();
tree.modify(1, d.get(x1)!, d.get(x2)! - 1, k);
y0 = y;
}
const target = area / 2.0;
area = 0.0;
y0 = 0;
for (const [y, x1, x2, k] of segs) {
const curLen = tree.query();
const t = (y - y0) * curLen;
if (area + t >= target) {
return y0 + (target - area) / curLen;
}
area += t;
tree.modify(1, d.get(x1)!, d.get(x2)! - 1, k);
y0 = y;
}
return 0.0;
}
时间复杂度 $O(n \times \log n)$,空间复杂度 $O(n)$。其中 $n$ 是正方形的数量。
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈 😄~



 {:width=400}
{:width=400} {:width=300}
{:width=300} ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
> ,
, ,
, ,
, ,
, ,
, ,
, >
>