方法一:浮点二分
所有正方形的面积之和为
$$
\textit{totalArea} = \sum_{i=0}^{n-1} l_i^2
$$
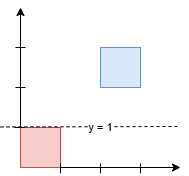
设在水平线 $Y=y$ 下方的面积之和为 $\textit{area}_y$,那么水平线上方的面积之和为 $\textit{totalArea}-\textit{area}_y$。
题目要求
$$
\textit{area}_y = \textit{totalArea}-\textit{area}_y
$$
即
$$
\textit{area}_y\cdot 2 = \textit{totalArea}
$$
我们可以二分最小的 $y$,满足
$$
\textit{area}_y\cdot 2 \ge \textit{totalArea}
$$
$\textit{area}_y$ 怎么算?
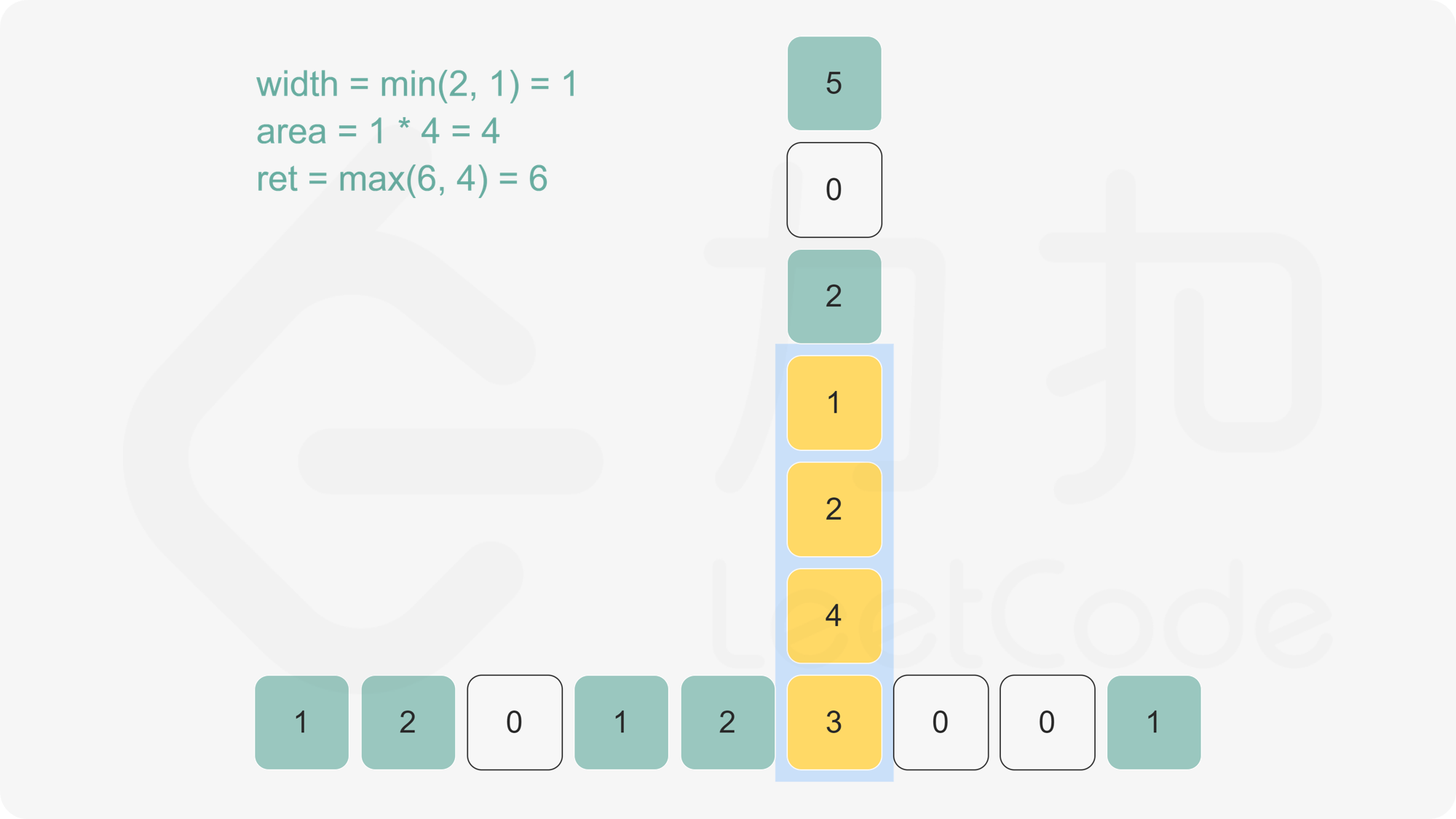
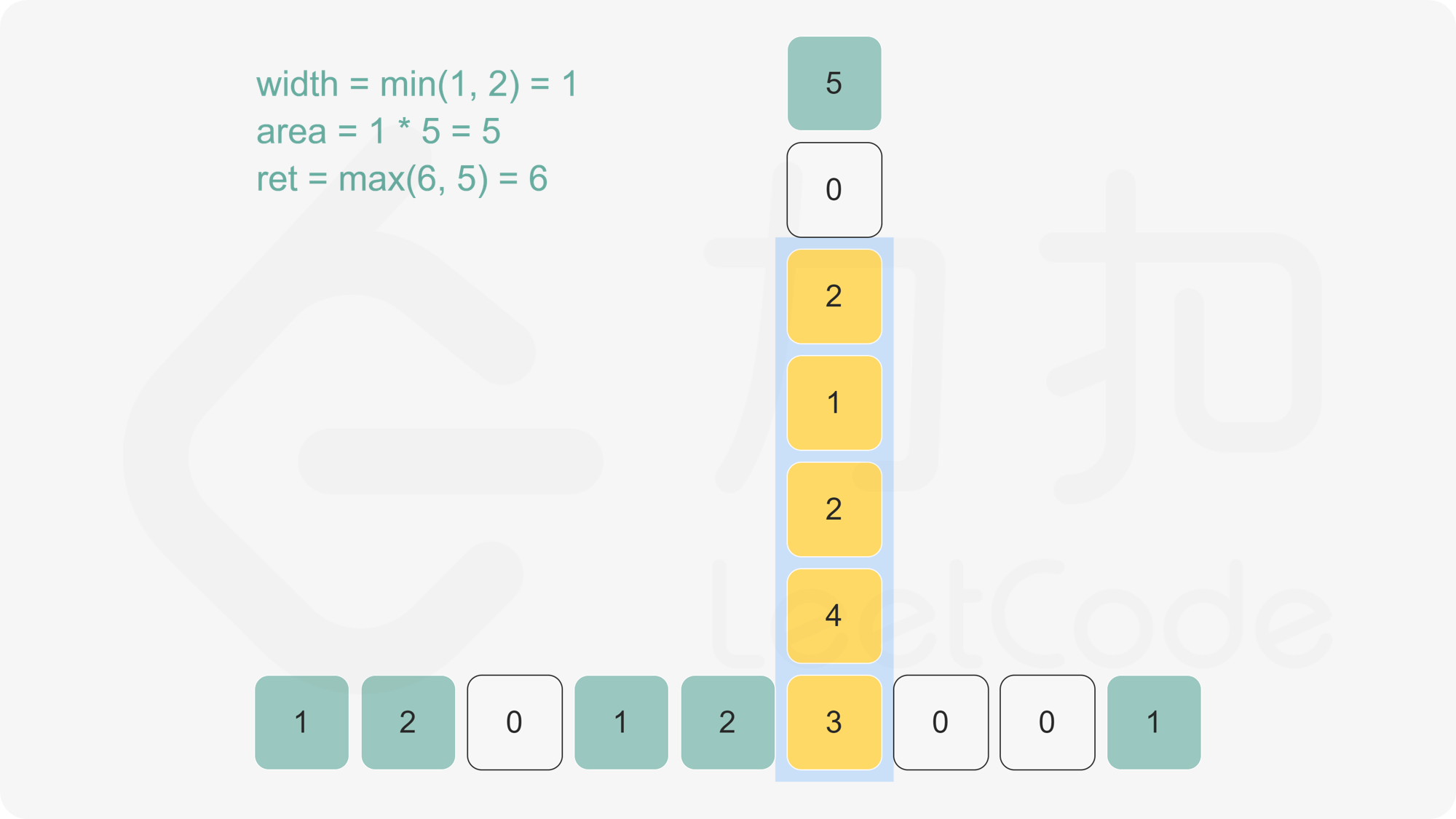
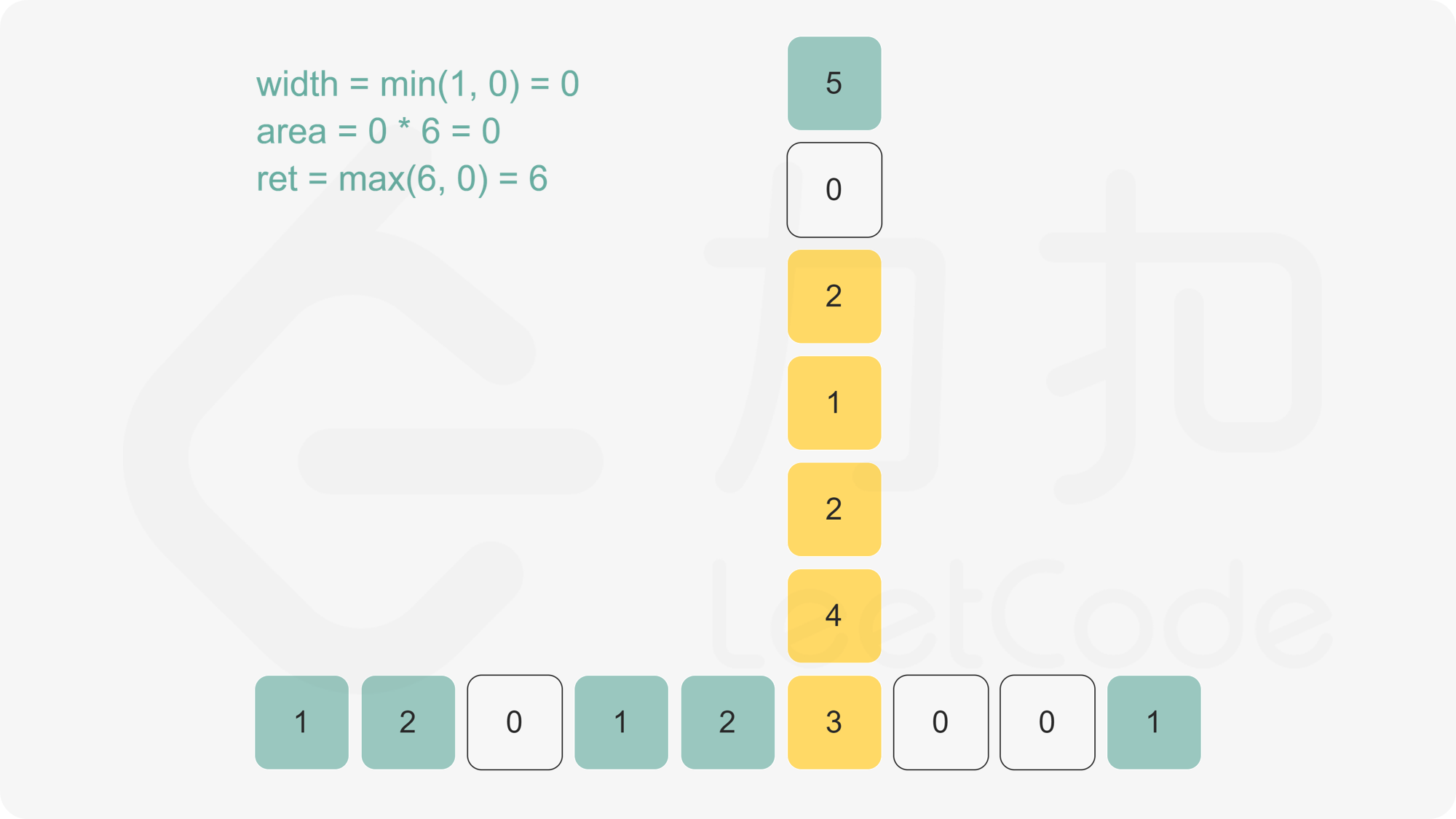
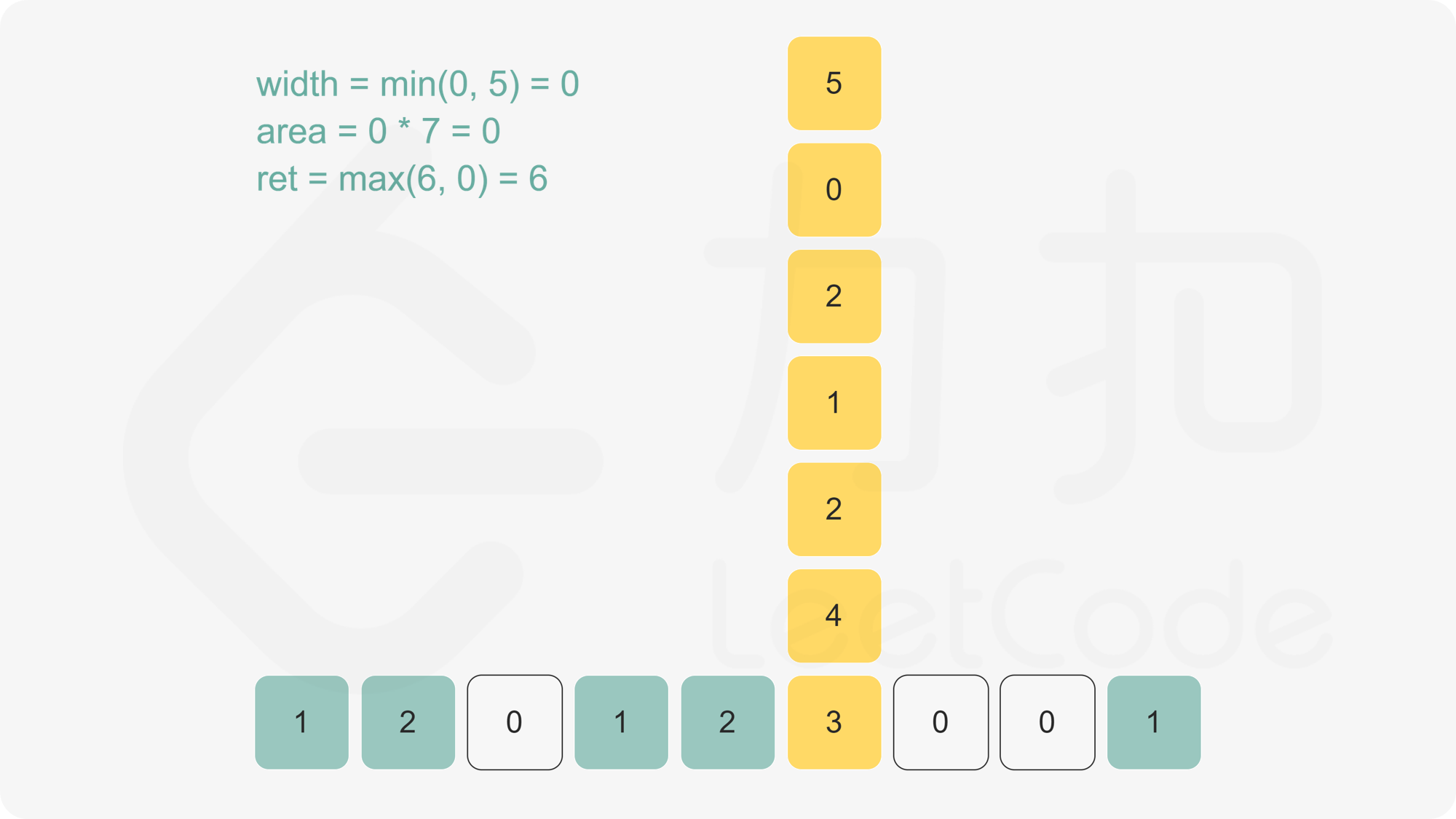
枚举正方形 $(x_i,y_i,l_i)$,如果水平线在正方形底边上面,即 $y_i < y$,那么这个正方形在水平线下方的面积为
$$
l_i\cdot\min(y-y_i, l_i)
$$
否则在水平线下方的面积为 $0$。总的来说就是
$$
l_i\cdot\min(\max(y-y_i,0), l_i)
$$
在水平线下方的总面积为
$$
\textit{area}y = \sum{i=0}^{n-1} l_i\cdot\min(\max(y-y_i,0), l_i)
$$
细节
二分的左边界为 $0$,右边界为 $\max(y_i+l_i)$。这里无需讨论开闭区间,因为我们算的是小数。
循环条件怎么写?
推荐的写法是固定一个循环次数,因为浮点数有舍入误差,可能算出的 $\textit{mid}$ 和 $\textit{left}$ 相等,此时 $\textit{left}=\textit{mid}$ 不会更新 $\textit{left}$,导致死循环。
注:本题由于值域小,也可以在 $\textit{left}$ 和 $\textit{right}$ 相距小于 $10^{-5}$ 时结束循环。但这种做法无法用于值域较大的场景,所以不推荐。
循环多少次?
设初始二分区间长度为 $L$,每二分一次,二分区间长度减半。要至少减半到 $10^{-5}$ 才能满足题目的误差要求。设循环次数为 $k$,我们有
$$
\dfrac{L}{2^k} \le 10^{-5}
$$
解得
$$
k\ge \log_2 (L\cdot 10^5)
$$
在本题的数据范围下,可以取 $k=48$(或者 $47$,取决于代码实现方式)。
本题视频讲解,欢迎点赞关注~
###py
class Solution:
def separateSquares(self, squares: List[List[int]]) -> float:
M = 100_000
total_area = sum(l * l for _, _, l in squares)
def check(y: float) -> bool:
area = 0
for _, yi, l in squares:
if yi < y:
area += l * min(y - yi, l)
return area >= total_area / 2
left = 0
right = max_y = max(y + l for _, y, l in squares)
for _ in range((max_y * M).bit_length()):
mid = (left + right) / 2
if check(mid):
right = mid
else:
left = mid
return (left + right) / 2 # 区间中点误差小
###java
class Solution {
public double separateSquares(int[][] squares) {
long totArea = 0;
int maxY = 0;
for (int[] sq : squares) {
int l = sq[2];
totArea += (long) l * l;
maxY = Math.max(maxY, sq[1] + l);
}
double left = 0;
double right = maxY;
for (int i = 0; i < 47; i++) {
double mid = (left + right) / 2;
if (check(squares, mid, totArea)) {
right = mid;
} else {
left = mid;
}
}
return (left + right) / 2; // 区间中点误差小
}
private boolean check(int[][] squares, double y, long totArea) {
double area = 0;
for (int[] sq : squares) {
double yi = sq[1];
if (yi < y) {
double l = sq[2];
area += l * Math.min(y - yi, l);
}
}
return area >= totArea / 2.0;
}
}
###cpp
class Solution {
public:
double separateSquares(vector<vector<int>>& squares) {
long long tot_area = 0;
int max_y = 0;
for (auto& sq : squares) {
int l = sq[2];
tot_area += 1LL * l * l;
max_y = max(max_y, sq[1] + l);
}
auto check = [&](double y) -> bool {
double area = 0;
for (auto& sq : squares) {
double yi = sq[1];
if (yi < y) {
double l = sq[2];
area += l * min(y - yi, l);
}
}
return area >= tot_area / 2.0;
};
double left = 0, right = max_y;
for (int i = 0; i < 47; i++) {
double mid = (left + right) / 2;
(check(mid) ? right : left) = mid;
}
return (left + right) / 2; // 区间中点误差小
}
};
###go
func separateSquares(squares [][]int) float64 {
totArea := 0
maxY := 0
for _, sq := range squares {
l := sq[2]
totArea += l * l
maxY = max(maxY, sq[1]+l)
}
check := func(y float64) bool {
area := 0.
for _, sq := range squares {
yi := float64(sq[1])
if yi < y {
l := float64(sq[2])
area += l * min(y-yi, l)
}
}
return area >= float64(totArea)/2
}
left, right := 0., float64(maxY)
for range bits.Len(uint(maxY * 1e5)) {
mid := (left + right) / 2
if check(mid) {
right = mid
} else {
left = mid
}
}
return (left + right) / 2 // 区间中点误差小
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n\log (MU))$,其中 $n$ 是 $\textit{squares}$ 的长度,$M=10^5$,$U=\max(y_i+l_i)$。
- 空间复杂度:$\mathcal{O}(1)$。
方法二:整数二分(写法一)
1)
方法一的 $y$ 是个小数。
记 $M = 10^5$,改为二分整数 $y\cdot M$,最后把二分结果再除以 $M$,即为答案。
在使用整数计算的前提下,这可以保证返回结果与正确答案的绝对误差严格小于 $1/M=10^{-5}$。
2)
下面代码采用开区间二分,这仅仅是二分的一种写法,使用闭区间或者半闭半开区间都是可以的。
- 开区间左端点初始值:$0$。无法满足要求。
- 开区间右端点初始值:$\max(y_i+l_i) \cdot M$。一定满足要求。
3)
能否全程使用整数计算?(只在返回的时候计算浮点数)
设当前二分的整数值为 $\textit{multiY}$,那么水平线下方的面积为
$$
\begin{aligned}
& l_i\cdot\min\left(\max\left(\dfrac{\textit{multiY}}{M}-y_i,0\right), l_i\right) \
={} & \dfrac{l_i\cdot\min(\max(\textit{multiY}-y_i\cdot M,0), l_i \cdot M)}{M} \
\end{aligned}
$$
所以有
$$
\textit{area}y = \dfrac{1}{M} \sum{i=0}^{n-1} l_i\cdot\min(\max(\textit{multiY}-y_i\cdot M,0),l_i \cdot M)
$$
判定条件
$$
\textit{area}_y\cdot 2 \ge \textit{totalArea}
$$
可以改为
$$
2 \sum_{i=0}^{n-1} l_i\cdot\min(\max(\textit{multiY}-y_i\cdot M,0), l_i\cdot M)\ge \textit{totalArea}\cdot M
$$
这样就可以全程使用整数计算了,只在最终返回时用到了浮点数。
###py
class Solution:
def separateSquares(self, squares: List[List[int]]) -> float:
M = 100_000
total_area = sum(l * l for _, _, l in squares)
def check(multi_y: int) -> bool:
area = 0
for _, y, l in squares:
if y * M < multi_y:
area += l * min(multi_y - y * M, l * M)
return area * 2 >= total_area * M
max_y = max(y + l for _, y, l in squares)
return bisect_left(range(max_y * M), True, key=check) / M
###java
class Solution {
private static final int M = 100_000;
public double separateSquares(int[][] squares) {
long totArea = 0;
int maxY = 0;
for (int[] sq : squares) {
int l = sq[2];
totArea += (long) l * l;
maxY = Math.max(maxY, sq[1] + l);
}
long left = 0;
long right = (long) maxY * M;
while (left + 1 < right) {
long mid = (left + right) >>> 1;
if (check(squares, mid, totArea)) {
right = mid;
} else {
left = mid;
}
}
return (double) right / M;
}
private boolean check(int[][] squares, long multiY, double totArea) {
long area = 0;
for (int[] sq : squares) {
long y = sq[1];
if (y * M < multiY) {
long l = sq[2];
area += l * Math.min(multiY - y * M, l * M);
}
}
return area * 2 >= totArea * M;
}
}
###cpp
class Solution {
public:
double separateSquares(vector<vector<int>>& squares) {
long long tot_area = 0;
int max_y = 0;
for (auto& sq : squares) {
int l = sq[2];
tot_area += 1LL * l * l;
max_y = max(max_y, sq[1] + l);
}
const int M = 100'000;
auto check = [&](long long multi_y) -> bool {
long long area = 0;
for (auto& sq : squares) {
long long y = sq[1];
if (y * M < multi_y) {
long long l = sq[2];
area += l * min(multi_y - y * M, l * M);
}
}
return area * 2 >= tot_area * M;
};
long long left = 0, right = 1LL * max_y * M;
while (left + 1 < right) {
long long mid = left + (right - left) / 2;
(check(mid) ? right : left) = mid;
}
return 1.0 * right / M;
}
};
###go
func separateSquares(squares [][]int) float64 {
totArea := 0
maxY := 0
for _, sq := range squares {
l := sq[2]
totArea += l * l
maxY = max(maxY, sq[1]+l)
}
const m = 100_000
multiY := sort.Search(maxY*m, func(multiY int) bool {
area := 0
for _, sq := range squares {
y, l := sq[1], sq[2]
if y*m < multiY {
area += l * min(multiY-y*m, l*m)
}
}
return area*2 >= totArea*m
})
return float64(multiY) / m
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n\log (MU))$,其中 $n$ 是 $\textit{squares}$ 的长度,$M=10^5$,$U=\max(y_i+l_i)$。
- 空间复杂度:$\mathcal{O}(1)$。
方法二:整数二分(写法二)
改成在 $0$ 到 $\max(y_i+l_i)$ 中二分最小的整数 $y$,满足
$$
\textit{area}_y\cdot 2 \ge \textit{totalArea}
$$
那么答案就在整数 $y-1$ 到整数 $y$ 之间。
由于输入都是整数,所以从 $y-1$ 到 $y$,在水平线下方的面积和是线性增加的,我们可以直接把答案解出来。
由于从 $y-1$ 到 $y$,矩形的底边长之和不变,所以用矩形面积的增量,除以矩形的高 $y-(y-1)=1$,就是矩形的底边长之和
$$
\textit{sumL} = \textit{area}y - \textit{area}{y-1}
$$
设答案为 $y'$,那么
$$
\textit{area}_{y'} = \textit{area}_y - (y-y')\cdot \textit{sumL}
$$
题目要求
$$
\textit{area}_{y'} \cdot 2 = \textit{totalArea}
$$
解得
$$
y' = y - \dfrac{\textit{area}_y - \textit{totalArea}/2}{\textit{sumL}} = y - \dfrac{\textit{area}_y\cdot 2 - \textit{totalArea}}{\textit{sumL}\cdot 2}
$$
###py
class Solution:
def separateSquares(self, squares: List[List[int]]) -> float:
def calc_area(y: int) -> int:
area = 0
for _, yi, l in squares:
if yi < y:
area += l * min(y - yi, l)
return area
tot_area = sum(l * l for _, _, l in squares)
max_y = max(y + l for _, y, l in squares)
y = bisect_left(range(max_y), tot_area, key=lambda y: calc_area(y) * 2)
area_y = calc_area(y)
sum_l = area_y - calc_area(y - 1)
return y - (area_y * 2 - tot_area) / (sum_l * 2) # 这样写误差更小
###java
class Solution {
public double separateSquares(int[][] squares) {
long totArea = 0;
int maxY = 0;
for (int[] sq : squares) {
int l = sq[2];
totArea += (long) l * l;
maxY = Math.max(maxY, sq[1] + l);
}
int left = 0;
int right = maxY;
while (left + 1 < right) {
int mid = (left + right) >>> 1;
if (calcArea(squares, mid) * 2 >= totArea) {
right = mid;
} else {
left = mid;
}
}
int y = right;
long areaY = calcArea(squares, y);
long sumL = areaY - calcArea(squares, y - 1);
return y - (areaY * 2 - totArea) / (sumL * 2.0); // 这样写误差更小
}
private long calcArea(int[][] squares, int y) {
long area = 0;
for (int[] sq : squares) {
int yi = sq[1];
if (yi < y) {
int l = sq[2];
area += (long) l * Math.min(y - yi, l);
}
}
return area;
}
}
###cpp
class Solution {
public:
double separateSquares(vector<vector<int>>& squares) {
long long tot_area = 0;
int max_y = 0;
for (auto& sq : squares) {
int l = sq[2];
tot_area += 1LL * l * l;
max_y = max(max_y, sq[1] + l);
}
auto calc_area = [&](int y) {
long long area = 0;
for (auto& sq : squares) {
int yi = sq[1];
if (yi < y) {
int l = sq[2];
area += 1LL * l * min(y - yi, l);
}
}
return area;
};
int left = 0, right = max_y;
while (left + 1 < right) {
int mid = left + (right - left) / 2;
(calc_area(mid) * 2 >= tot_area ? right : left) = mid;
}
int y = right;
long long area_y = calc_area(y);
long long sum_l = area_y - calc_area(y - 1);
return y - (area_y * 2 - tot_area) / (sum_l * 2.0); // 这样写误差更小
}
};
###go
func separateSquares(squares [][]int) float64 {
totArea := 0
maxY := 0
for _, sq := range squares {
l := sq[2]
totArea += l * l
maxY = max(maxY, sq[1]+l)
}
calcArea := func(y int) (area int) {
for _, sq := range squares {
yi := sq[1]
if yi < y {
l := sq[2]
area += l * min(y-yi, l)
}
}
return
}
y := sort.Search(maxY, func(y int) bool { return calcArea(y)*2 >= totArea })
areaY := calcArea(y)
sumL := areaY - calcArea(y-1)
return float64(y) - float64(areaY*2-totArea)/float64(sumL*2) // 这样写误差更小
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n\log U)$,其中 $n$ 是 $\textit{squares}$ 的长度,$U=\max(y_i+l_i)$。
- 空间复杂度:$\mathcal{O}(1)$。
方法三:差分+扫描线

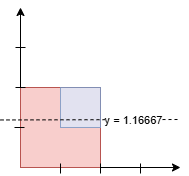
想象有一根水平扫描线在从下往上扫描,对于示例 2,这根扫描线依次扫过 $y=0,1,2$:
- 从 $y=0$ 到 $y=1$,面积的增加量可以视作一个底边长为 $2$,高为 $1$ 的矩形的面积,即 $2\cdot 1 = 2$。
- 从 $y=1$ 到 $y=2$,面积的增加量可以视作一个底边长为 $2+1=3$(重叠的要累加),高为 $1$ 的矩形的面积,即 $3\cdot 1 = 3$。
扫描的过程中,维护面积之和 $\textit{area}$,底边长之和 $\textit{sumL}$。
设当前 $y$ 与下一个 $y'$ 之差为 $y'-y$,则新增面积为
$$
\textit{sumL}\cdot (y'-y)
$$
如果发现
$$
\textit{area} \cdot 2 \ge \textit{totalArea}
$$
那么可以直接算出答案,计算公式和上面「方法二:整数二分(写法二)」是一样的。
$\textit{sumL}$ 可以用差分维护。原理讲解,推荐和【图解】从一维差分到二维差分 一起看。
###py
class Solution:
def separateSquares(self, squares: List[List[int]]) -> float:
tot_area = 0
diff = defaultdict(int)
for _, y, l in squares:
tot_area += l * l
diff[y] += l
diff[y + l] -= l
area = sum_l = 0
for y, y2 in pairwise(sorted(diff)):
sum_l += diff[y] # 矩形底边长度之和
area += sum_l * (y2 - y) # 底边长 * 高 = 新增面积
if area * 2 >= tot_area:
return y2 - (area * 2 - tot_area) / (sum_l * 2)
###java
class Solution {
public double separateSquares(int[][] squares) {
long totArea = 0;
TreeMap<Integer, Long> diff = new TreeMap<>();
for (int[] sq : squares) {
int y = sq[1];
long l = sq[2];
totArea += l * l;
diff.merge(y, l, Long::sum);
diff.merge(y + (int) l, -l, Long::sum);
}
long area = 0;
long sumL = 0;
int preY = 0; // 不好计算下一个 y,改成维护上一个 y
for (var e : diff.entrySet()) {
int y = e.getKey();
area += sumL * (y - preY); // 底边长 * 高 = 新增面积
if (area * 2 >= totArea) {
return y - (area * 2 - totArea) / (sumL * 2.0);
}
preY = y;
sumL += e.getValue(); // 矩形底边长度之和
}
return -1;
}
}
###cpp
class Solution {
public:
double separateSquares(vector<vector<int>>& squares) {
long long tot_area = 0;
map<int, long long> diff;
for (auto& sq : squares) {
int y = sq[1], l = sq[2];
tot_area += 1LL * l * l;
diff[y] += l;
diff[y + l] -= l;
}
long long area = 0, sum_l = 0;
for (auto it = diff.begin();;) {
auto [y, sl] = *it;
int y2 = (++it)->first;
sum_l += sl; // 矩形底边长度之和
area += sum_l * (y2 - y); // 底边长 * 高 = 新增面积
if (area * 2 >= tot_area) {
return y2 - (area * 2 - tot_area) / (sum_l * 2.0);
}
}
}
};
###go
func separateSquares(squares [][]int) float64 {
totArea := 0
diff := map[int]int{}
for _, sq := range squares {
y, l := sq[1], sq[2]
totArea += l * l
diff[y] += l
diff[y+l] -= l
}
ys := slices.Sorted(maps.Keys(diff))
area, sumL := 0, 0
for i := 0; ; i++ {
sumL += diff[ys[i]] // 矩形底边长度之和
area += sumL * (ys[i+1] - ys[i]) // 底边长 * 高 = 新增面积
if area*2 >= totArea {
return float64(ys[i+1]) - float64(area*2-totArea)/float64(sumL*2)
}
}
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n\log n)$,其中 $n$ 是 $\textit{squares}$ 的长度。瓶颈在排序/维护有序集合上。
- 空间复杂度:$\mathcal{O}(n)$。
分类题单
如何科学刷题?
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 【本题相关】二分算法(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/最短路/最小生成树/二分图/基环树/欧拉路径)
- 动态规划(入门/背包/状态机/划分/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、二叉树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA/一般树)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)
我的题解精选(已分类)


 {:width=400}
{:width=400} {:width=300}
{:width=300} ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
> ,
, ,
, ,
, ,
, ,
, ,
, >
>





 {:width=360px}
{:width=360px}