核心思路
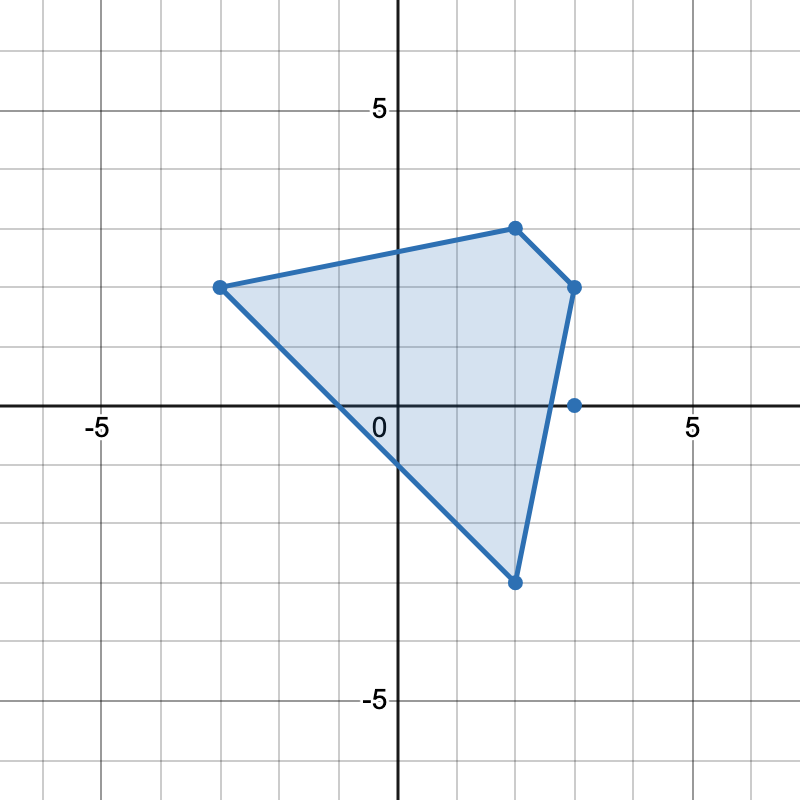
- 本题 $n\le 500$,我们可以 $\mathcal{O}(n^2)$ 枚举所有点对组成的直线,计算直线的斜率和截距。
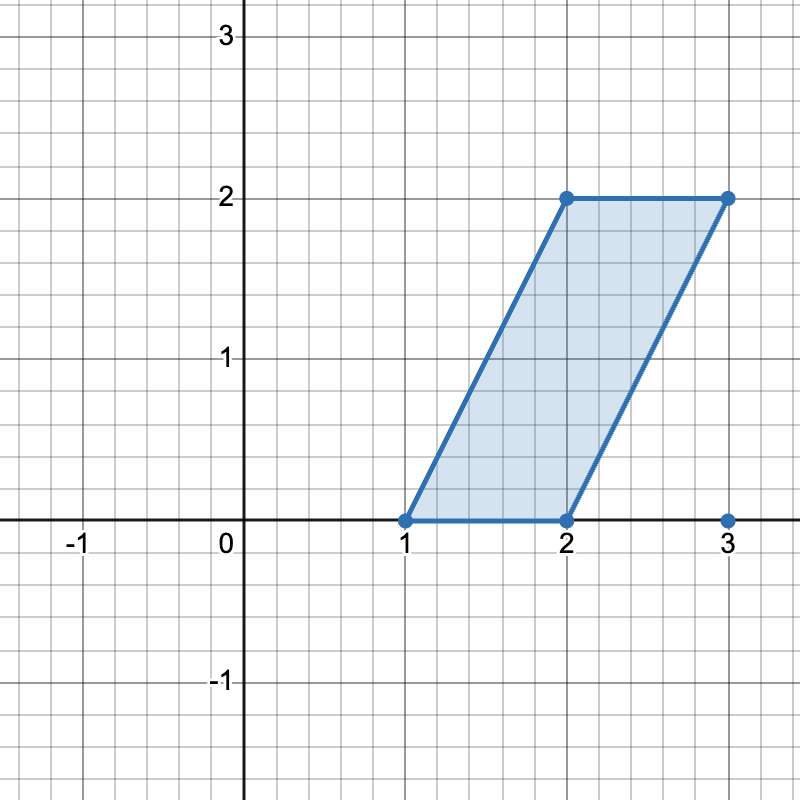
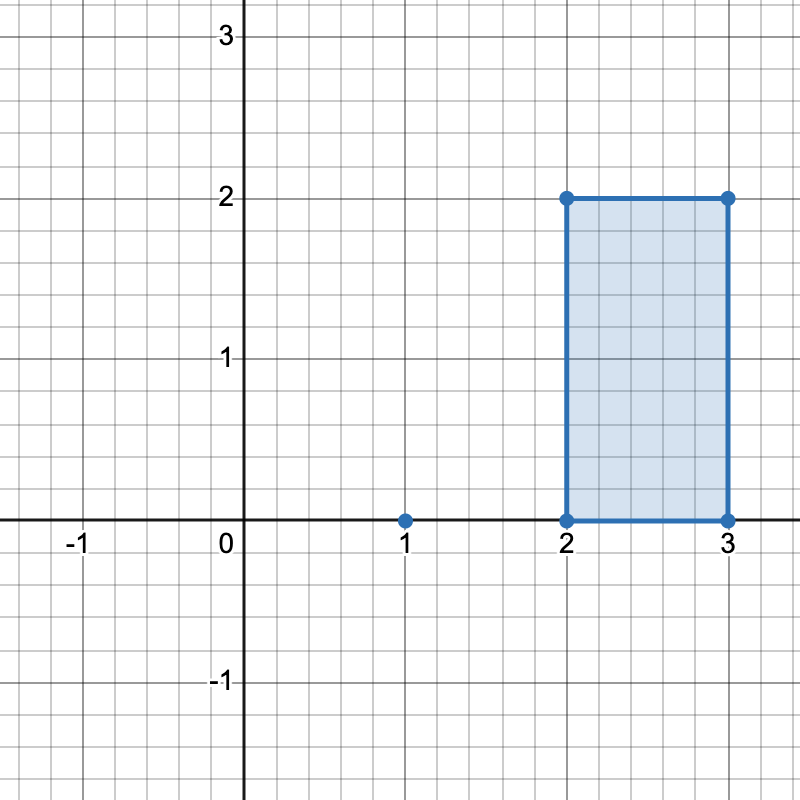
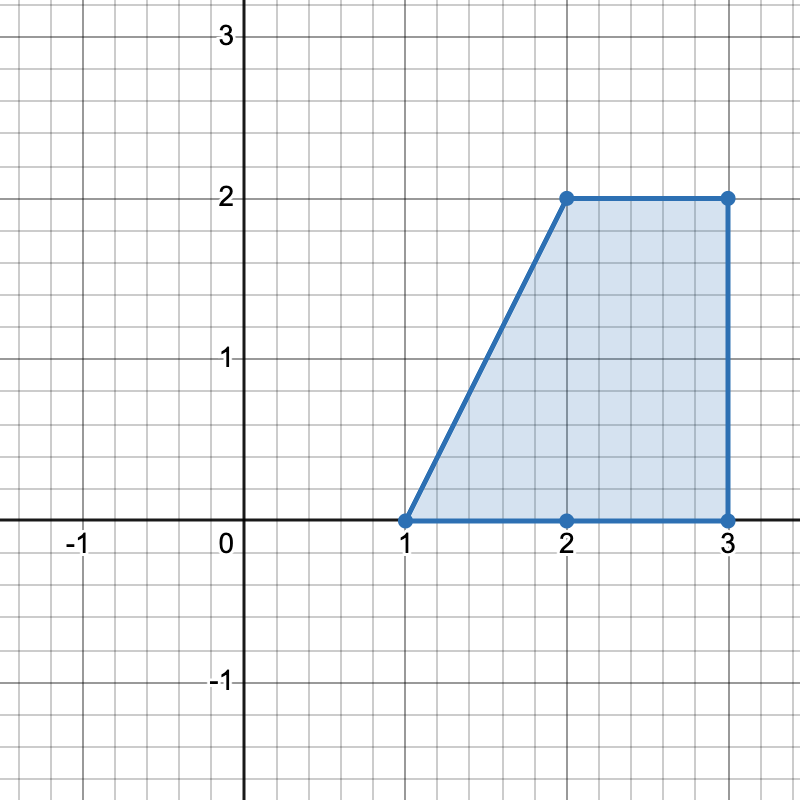
- 把斜率相同的直线放在同一组,可以从中选择一对平行边,作为梯形的顶边和底边。⚠注意:不能选两条重合的边,所以还要按照截距分组,同一组内的边不能选。
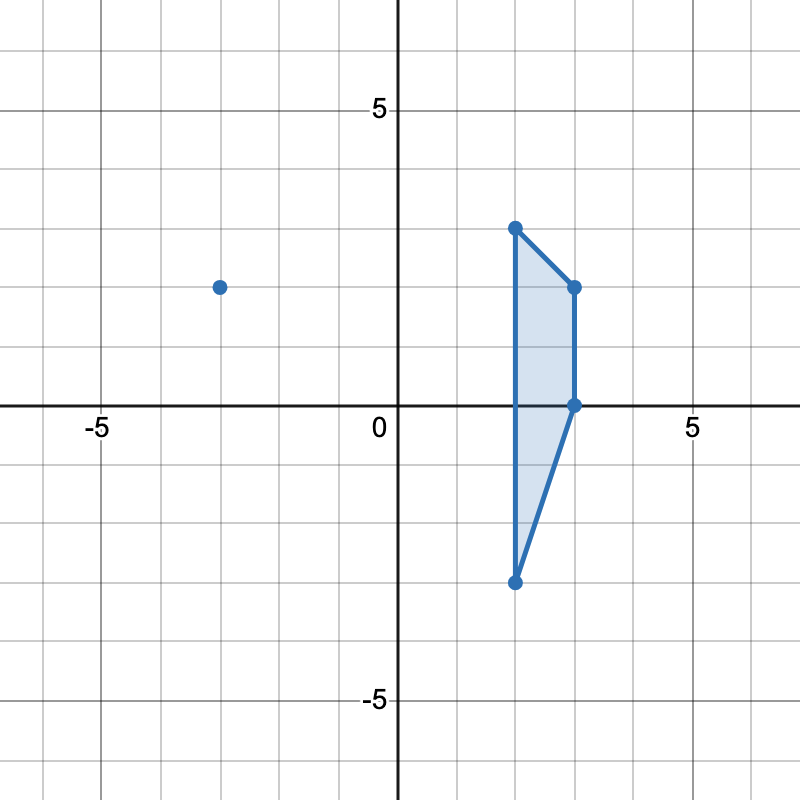
- 第二步把平行四边形重复统计了一次,所以还要减去任意不共线四点组成的平行四边形的个数。
具体思路
1) 计算直线的斜率和截距
对于两个点 $(x,y)$ 和 $(x_2,y_2)$,设 $\textit{dx} = x - x_2$,$\textit{dy} = y - y_2$。
经过这两个点的斜率为
$$
k =
\begin{cases}
\dfrac{\textit{dy}}{\textit{dx}}, & \textit{dx}\ne 0 \
\infty, & \textit{dx} = 0 \
\end{cases}
$$
当 $\textit{dx} \ne 0$ 时,设直线为 $Y = k\cdot X + b$,把 $(x,y)$ 代入,解得截距
$$
b = y - k\cdot x = \dfrac{y\cdot \textit{dx}-x\cdot \textit{dy}}{\textit{dx}}
$$
当 $\textit{dx} = 0$ 时,直线平行于 $y$ 轴,人为规定 $b=x$,用来区分不同的平行线。
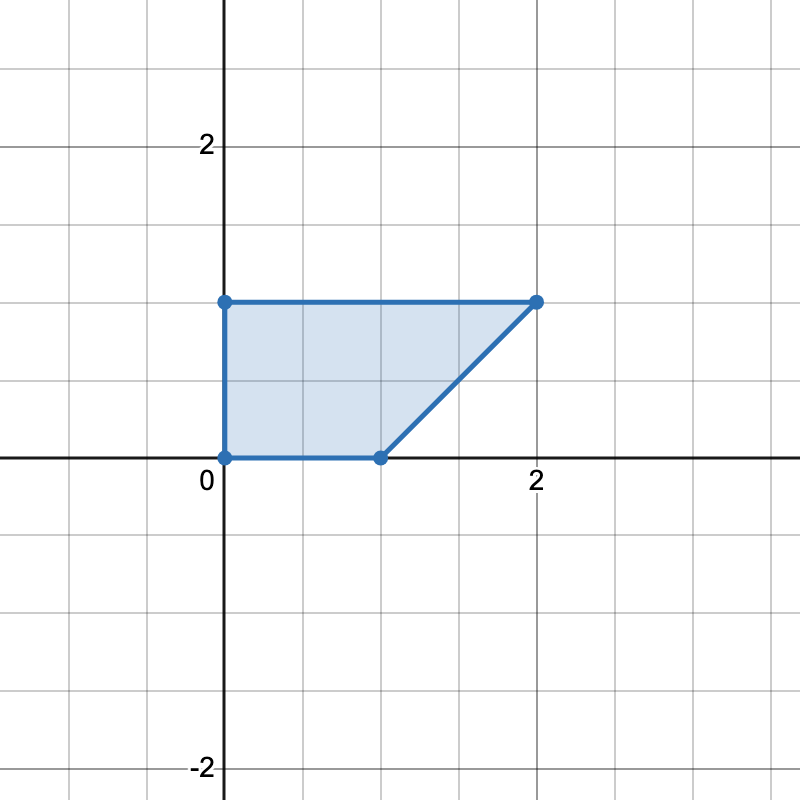
2) 选择一对平行边的方案数
把斜率相同的直线放在同一组,可以从中选择一对平行线,作为梯形的顶边和底边。
⚠注意:不能选两条共线的线段,所以斜率相同的组内,还要再按照截距分组,相同斜率和截距的边不能同时选。
用哈希表套哈希表统计。
统计完后,对于每一组,用「枚举右,维护左」的思想(见周赛第二题 3623. 统计梯形的数目 I),计算选一对平行边的方案数。本题由于哈希表统计的就是线段个数,所以不需要计算 $\dfrac{c(c-1)}{2}$。
3) 平行四边形的个数
第二步把平行四边形重复统计了一次,所以还要减去任意不共线四点组成的平行四边形的个数。
怎么计算平行四边形的个数?
对于平行四边形,其两条对角线的中点是重合的。利用这一性质,按照对角线的中点分组统计。
具体地,两个点 $(x,y)$ 和 $(x_2,y_2)$ 的中点为
$$
\left(\dfrac{x+x_2}{2}, \dfrac{y+y_2}{2}\right)
$$
为避免浮点数,可以把横纵坐标都乘以 $2$(这不影响分组),即
$$
(x+x_2, y+y_2)
$$
用其作为哈希表的 key。
同样地,我们不能选两条共线的线段,所以中点相同的组内,还要再按照斜率分组,相同斜率的边不能同时选。所以同样地,用哈希表套哈希表统计。
统计完后,对于每一组,用「枚举右,维护左」的思想(见周赛第二题),计算选一对中点相同的线段的方案数。
注意计算梯形个数我们用的是顶边和底边,计算平行四边形个数我们用的是对角线。
答疑
问:什么情况下用浮点数是错的?
答:取两个接近 $1$ 但不相同的分数 $\dfrac{a}{a+1}$ 和 $\dfrac{a-1}{a}$,根据 IEEE 754,在使用双精度浮点数的情况下,如果这两个数的绝对差 $\dfrac{1}{a(a+1)}$ 比 $2^{-52}$ 还小,那么计算机可能会把这两个数舍入到同一个附近的浮点数上。所以当 $a$ 达到 $2^{26}\approx 6.7\cdot 10^7$ 的时候,用浮点数就不一定对了。本题数据范围只有 $2\cdot 10^3$,可以放心地使用浮点数除法。
具体请看 视频讲解,欢迎点赞关注~
优化前
###py
class Solution:
def countTrapezoids(self, points: List[List[int]]) -> int:
cnt = defaultdict(lambda: defaultdict(int)) # 斜率 -> 截距 -> 个数
cnt2 = defaultdict(lambda: defaultdict(int)) # 中点 -> 斜率 -> 个数
for i, (x, y) in enumerate(points):
for x2, y2 in points[:i]:
dy = y - y2
dx = x - x2
k = dy / dx if dx else inf
b = (y * dx - x * dy) / dx if dx else x
cnt[k][b] += 1 # 按照斜率和截距分组
cnt2[(x + x2, y + y2)][k] += 1 # 按照中点和斜率分组
ans = 0
for m in cnt.values():
s = 0
for c in m.values():
ans += s * c
s += c
for m in cnt2.values():
s = 0
for c in m.values():
ans -= s * c # 平行四边形会统计两次,减去多统计的一次
s += c
return ans
###java
class Solution {
public int countTrapezoids(int[][] points) {
Map<Double, Map<Double, Integer>> cnt = new HashMap<>(); // 斜率 -> 截距 -> 个数
Map<Integer, Map<Double, Integer>> cnt2 = new HashMap<>(); // 中点 -> 斜率 -> 个数
int n = points.length;
for (int i = 0; i < n; i++) {
int x = points[i][0], y = points[i][1];
for (int j = 0; j < i; j++) {
int x2 = points[j][0], y2 = points[j][1];
int dy = y - y2;
int dx = x - x2;
double k = dx != 0 ? 1.0 * dy / dx : Double.MAX_VALUE;
double b = dx != 0 ? 1.0 * (y * dx - x * dy) / dx : x;
// 归一化 -0.0 为 0.0
if (k == -0.0) {
k = 0.0;
}
if (b == -0.0) {
b = 0.0;
}
// 按照斜率和截距分组 cnt[k][b]++
cnt.computeIfAbsent(k, _ -> new HashMap<>()).merge(b, 1, Integer::sum);
int mid = (x + x2 + 2000) * 10000 + (y + y2 + 2000); // 把二维坐标压缩成一个 int
// 按照中点和斜率分组 cnt2[mid][k]++
cnt2.computeIfAbsent(mid, _ -> new HashMap<>()).merge(k, 1, Integer::sum);
}
}
int ans = 0;
for (Map<Double, Integer> m : cnt.values()) {
int s = 0;
for (int c : m.values()) {
ans += s * c;
s += c;
}
}
for (Map<Double, Integer> m : cnt2.values()) {
int s = 0;
for (int c : m.values()) {
ans -= s * c; // 平行四边形会统计两次,减去多统计的一次
s += c;
}
}
return ans;
}
}
###cpp
class Solution {
public:
int countTrapezoids(vector<vector<int>>& points) {
// 经测试,哈希表套 map 比哈希表套哈希表更快(分组后,每一组的数据量比较小,在小数据下 map 比哈希表快)
unordered_map<double, map<double, int>> cnt; // 斜率 -> 截距 -> 个数
unordered_map<int, map<double, int>> cnt2; // 中点 -> 斜率 -> 个数
int n = points.size();
for (int i = 0; i < n; i++) {
int x = points[i][0], y = points[i][1];
for (int j = 0; j < i; j++) {
int x2 = points[j][0], y2 = points[j][1];
int dy = y - y2;
int dx = x - x2;
double k = dx ? 1.0 * dy / dx : DBL_MAX;
double b = dx ? 1.0 * (y * dx - x * dy) / dx : x;
cnt[k][b]++; // 按照斜率和截距分组
int mid = (x + x2 + 2000) << 16 | (y + y2 + 2000); // 把二维坐标压缩成一个 int
cnt2[mid][k]++; // 按照中点和斜率分组
}
}
int ans = 0;
for (auto& [_, m] : cnt) {
int s = 0;
for (auto& [_, c] : m) {
ans += s * c;
s += c;
}
}
for (auto& [_, m] : cnt2) {
int s = 0;
for (auto& [_, c] : m) {
ans -= s * c; // 平行四边形会统计两次,减去多统计的一次
s += c;
}
}
return ans;
}
};
###go
func countTrapezoids(points [][]int) (ans int) {
cnt := map[float64]map[float64]int{} // 斜率 -> 截距 -> 个数
type pair struct{ x, y int }
cnt2 := map[pair]map[float64]int{} // 中点 -> 斜率 -> 个数
for i, p := range points {
x, y := p[0], p[1]
for _, q := range points[:i] {
x2, y2 := q[0], q[1]
dy := y - y2
dx := x - x2
k := math.MaxFloat64
b := float64(x)
if dx != 0 {
k = float64(dy) / float64(dx)
b = float64(y*dx-dy*x) / float64(dx)
}
if _, ok := cnt[k]; !ok {
cnt[k] = map[float64]int{}
}
cnt[k][b]++ // 按照斜率和截距分组
mid := pair{x + x2, y + y2}
if _, ok := cnt2[mid]; !ok {
cnt2[mid] = map[float64]int{}
}
cnt2[mid][k]++ // 按照中点和斜率分组
}
}
for _, m := range cnt {
s := 0
for _, c := range m {
ans += s * c
s += c
}
}
for _, m := range cnt2 {
s := 0
for _, c := range m {
ans -= s * c // 平行四边形会统计两次,减去多统计的一次
s += c
}
}
return
}
优化
上面做法最坏会创建 $\mathcal{O}(n^2)$ 个哈希表。这其实就是导致代码变慢的根源。
减少创建的哈希表个数,就能省下大量时间。
在随机数据下,对于相同的斜率 $k$,大概率只有一条线段,无法组成梯形。这些数据根本就不需要创建哈希表!
所以,先不创建内部的哈希表,而是先把数据保存到更轻量的列表中。在计算答案的时候,再去创建哈希表。对于大小为 $1$ 的列表,我们直接跳过,不创建哈希表。
###py
class Solution:
def countTrapezoids(self, points: List[List[int]]) -> int:
groups = defaultdict(list) # 斜率 -> [截距]
groups2 = defaultdict(list) # 中点 -> [斜率]
for i, (x, y) in enumerate(points):
for x2, y2 in points[:i]:
dy = y - y2
dx = x - x2
k = dy / dx if dx else inf
b = (y * dx - x * dy) / dx if dx else x
groups[k].append(b)
groups2[(x + x2, y + y2)].append(k)
ans = 0
for g in groups.values():
if len(g) == 1:
continue
s = 0
for c in Counter(g).values():
ans += s * c
s += c
for g in groups2.values():
if len(g) == 1:
continue
s = 0
for c in Counter(g).values():
ans -= s * c # 平行四边形会统计两次,减去多统计的一次
s += c
return ans
###java
class Solution {
public int countTrapezoids(int[][] points) {
Map<Double, List<Double>> groups = new HashMap<>(); // 斜率 -> [截距]
Map<Integer, List<Double>> groups2 = new HashMap<>(); // 中点 -> [斜率]
int n = points.length;
for (int i = 0; i < n; i++) {
int x = points[i][0], y = points[i][1];
for (int j = 0; j < i; j++) {
int x2 = points[j][0], y2 = points[j][1];
int dy = y - y2;
int dx = x - x2;
double k = dx != 0 ? 1.0 * dy / dx : Double.MAX_VALUE;
if (k == -0.0) {
k = 0.0;
}
double b = dx != 0 ? 1.0 * (y * dx - x * dy) / dx : x;
groups.computeIfAbsent(k, _ -> new ArrayList<>()).add(b);
int mid = (x + x2 + 2000) * 10000 + (y + y2 + 2000); // 把二维坐标压缩成一个 int
groups2.computeIfAbsent(mid, _ -> new ArrayList<>()).add(k);
}
}
int ans = 0;
Map<Double, Integer> cnt = new HashMap<>();
for (List<Double> g : groups.values()) {
if (g.size() == 1) {
continue;
}
cnt.clear();
for (double b : g) {
if (b == -0.0) {
b = 0.0;
}
cnt.merge(b, 1, Integer::sum);
}
int s = 0;
for (int c : cnt.values()) {
ans += s * c;
s += c;
}
}
for (List<Double> g : groups2.values()) {
if (g.size() == 1) {
continue;
}
cnt.clear();
for (double k : g) {
cnt.merge(k, 1, Integer::sum);
}
int s = 0;
for (int c : cnt.values()) {
ans -= s * c; // 平行四边形会统计两次,减去多统计的一次
s += c;
}
}
return ans;
}
}
###cpp
class Solution {
public:
int countTrapezoids(vector<vector<int>>& points) {
unordered_map<double, vector<double>> groups; // 斜率 -> [截距]
unordered_map<int, vector<double>> groups2; // 中点 -> [斜率]
int n = points.size();
for (int i = 0; i < n; i++) {
int x = points[i][0], y = points[i][1];
for (int j = 0; j < i; j++) {
int x2 = points[j][0], y2 = points[j][1];
int dy = y - y2;
int dx = x - x2;
double k = dx ? 1.0 * dy / dx : DBL_MAX;
double b = dx ? 1.0 * (y * dx - x * dy) / dx : x;
groups[k].push_back(b);
int mid = (x + x2 + 2000) << 16 | (y + y2 + 2000); // 把二维坐标压缩成一个 int
groups2[mid].push_back(k);
}
}
int ans = 0;
for (auto& [_, g] : groups) {
if (g.size() == 1) {
continue;
}
// 对于本题的数据,map 比哈希表快
map<double, int> cnt;
for (double b : g) {
cnt[b]++;
}
int s = 0;
for (auto& [_, c] : cnt) {
ans += s * c;
s += c;
}
}
for (auto& [_, g] : groups2) {
if (g.size() == 1) {
continue;
}
map<double, int> cnt;
for (double k : g) {
cnt[k]++;
}
int s = 0;
for (auto& [_, c] : cnt) {
ans -= s * c; // 平行四边形会统计两次,减去多统计的一次
s += c;
}
}
return ans;
}
};
###go
func countTrapezoids(points [][]int) (ans int) {
groups := map[float64][]float64{} // 斜率 -> [截距]
type pair struct{ x, y int }
groups2 := map[pair][]float64{} // 中点 -> [斜率]
for i, p := range points {
x, y := p[0], p[1]
for _, q := range points[:i] {
x2, y2 := q[0], q[1]
dy := y - y2
dx := x - x2
k := math.MaxFloat64
b := float64(x)
if dx != 0 {
k = float64(dy) / float64(dx)
b = float64(y*dx-dy*x) / float64(dx)
}
groups[k] = append(groups[k], b)
mid := pair{x + x2, y + y2}
groups2[mid] = append(groups2[mid], k)
}
}
for _, g := range groups {
if len(g) == 1 {
continue
}
cnt := map[float64]int{}
for _, b := range g {
cnt[b]++
}
s := 0
for _, c := range cnt {
ans += s * c
s += c
}
}
for _, g := range groups2 {
if len(g) == 1 {
continue
}
cnt := map[float64]int{}
for _, k := range g {
cnt[k]++
}
s := 0
for _, c := range cnt {
ans -= s * c // 平行四边形会统计两次,减去多统计的一次
s += c
}
}
return
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n^2)$,其中 $n$ 是 $\textit{points}$ 的长度。
- 空间复杂度:$\mathcal{O}(n^2)$。
思考题
- 梯形改成正方形怎么做?
- 梯形改成菱形怎么做?
- 梯形改成矩形怎么做?
- 梯形改成等腰梯形怎么做?
- 梯形改成直角梯形怎么做?
欢迎在评论区分享你的思路/代码。
分类题单
如何科学刷题?
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 二分算法(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流)
- 动态规划(入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)
我的题解精选(已分类)
欢迎关注 B站@灵茶山艾府