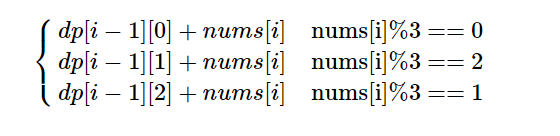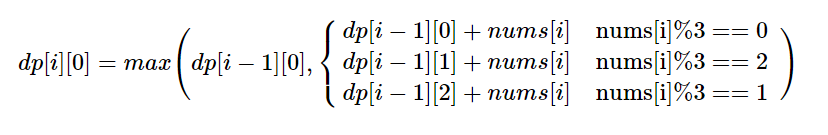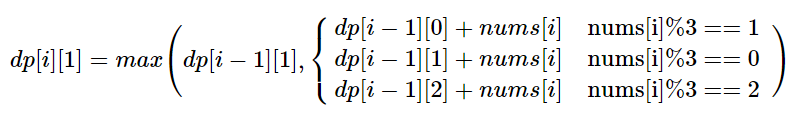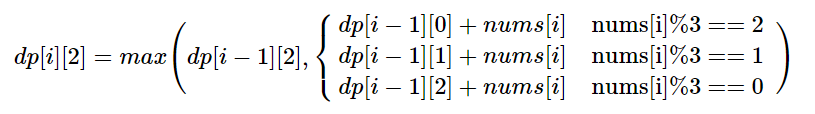给你一个整数数组 nums，请你找出并返回能被三整除的元素 最大和。
示例 1：
输入：nums = [3,6,5,1,8] 输出：18 解释：选出数字 3, 6, 1 和 8，它们的和是 18（可被 3 整除的最大和）。
示例 2：
输入：nums = [4] 输出：0 解释：4 不能被 3 整除，所以无法选出数字，返回 0。
示例 3：
输入：nums = [1,2,3,4,4] 输出：12 解释：选出数字 1, 3, 4 以及 4，它们的和是 12（可被 3 整除的最大和）。
提示：
登录1 <= nums.length <= 4 * 1041 <= nums[i] <= 104由于数组中没有负数，如果整个数组的元素和 $s$ 可以被 $3$ 整除，那么 $s$ 就是最大的元素和。
否则，如果 $s$ 不能被 $3$ 整除，那就看看能否让 $s$ 减去某些 $\textit{nums}[i]$，使得 $s$ 可以被 $3$ 整除。
找到所有 $\textit{nums}[i]\bmod 3 = 1$ 的 $\textit{nums}[i]$，放到数组 $a_1$ 中；找到所有 $\textit{nums}[i]\bmod 3 = 2$ 的 $\textit{nums}[i]$，放到数组 $a_2$ 中。
对 $a_1$ 和 $a_2$ 从小到大排序。分类讨论：
代码实现时，如果 $s\bmod 3 = 2$，那么可以交换数组 $a_1$ 和 $a_2$，从而复用同一套逻辑。
但是，贪心算法是有局限的。试想一下，如果把题目中的 $3$ 换成 $4$，要如何分类讨论？换成 $5$，又要如何分类讨论？随着数字的变大，要讨论的内容越来越复杂。那么，是否有更加通用的做法呢？请继续阅读。
class Solution:
def maxSumDivThree(self, nums: List[int]) -> int:
s = sum(nums)
if s % 3 == 0:
return s
a1 = sorted(x for x in nums if x % 3 == 1)
a2 = sorted(x for x in nums if x % 3 == 2)
if s % 3 == 2:
a1, a2 = a2, a1
ans = s - a1[0] if a1 else 0
if len(a2) > 1:
ans = max(ans, s - a2[0] - a2[1])
return ans
class Solution {
public int maxSumDivThree(int[] nums) {
int s = 0;
for (int x : nums)
s += x;
if (s % 3 == 0)
return s;
var a1 = new ArrayList<Integer>();
var a2 = new ArrayList<Integer>();
for (int x : nums) {
if (x % 3 == 1) a1.add(x);
else if (x % 3 == 2) a2.add(x);
}
Collections.sort(a1);
Collections.sort(a2);
if (s % 3 == 2) { // swap(a1,a2)
var tmp = a1;
a1 = a2;
a2 = tmp;
}
int ans = a1.isEmpty() ? 0 : s - a1.get(0);
if (a2.size() > 1)
ans = Math.max(ans, s - a2.get(0) - a2.get(1));
return ans;
}
}
class Solution {
public:
int maxSumDivThree(vector<int> &nums) {
int s = accumulate(nums.begin(), nums.end(), 0);
if (s % 3 == 0)
return s;
vector<int> a[3];
for (int x: nums)
a[x % 3].push_back(x);
sort(a[1].begin(), a[1].end());
sort(a[2].begin(), a[2].end());
if (s % 3 == 2)
swap(a[1], a[2]);
int ans = a[1].size() ? s - a[1][0] : 0;
if (a[2].size() > 1)
ans = max(ans, s - a[2][0] - a[2][1]);
return ans;
}
};
func maxSumDivThree(nums []int) (ans int) {
s := 0
for _, x := range nums {
s += x
}
if s%3 == 0 {
return s
}
a := [3][]int{}
for _, x := range nums {
a[x%3] = append(a[x%3], x)
}
sort.Ints(a[1])
sort.Ints(a[2])
if s%3 == 2 {
a[1], a[2] = a[2], a[1]
}
if len(a[1]) > 0 {
ans = s - a[1][0]
}
if len(a[2]) > 1 {
ans = max(ans, s-a[2][0]-a[2][1])
}
return
}
func max(a, b int) int { if a < b { return b }; return a }
注：由于只要最小的两个数，可以做到 $\mathcal{O}(n)$ 时间和 $\mathcal{O}(1)$ 额外空间，但写起来较为复杂。考虑到动态规划的做法同样可以做到 $\mathcal{O}(n)$ 时间和 $\mathcal{O}(1)$ 额外空间，所以这里就不进一步优化了。
详见 动态规划入门：从记忆化搜索到递推【基础算法精讲 17】。
用「选或不选」的思路，考虑最后一个数 $x = \textit{nums}[n-1]$：
上述讨论，刻画了这道题的两个重要参数：
那么原问题就是 $(i=n-1, j=0)$，上述讨论得到的子问题有 $(i=n-2,j=0),\ (i=n-2,j=1),\ (i=n-2,j=2)$。
注：为什么要从最后一个数开始讨论？主要是为了方便后面把记忆化搜索改成递推。当然，从第一个数开始讨论也是可以的。
根据上面的讨论，定义 $\textit{dfs}(i,j)$ 表示从 $\textit{nums}[0]$ 到 $\textit{nums}[i]$ 中选数，后续还需要选的数字之和 $s$ 满足 $s\bmod 3 = j$ 的前提下，$s$ 的最大值。
设 $x=\textit{nums}[i]$，分类讨论：
这两种情况取最大值，有
$$
\textit{dfs}(i,j) = \max(\textit{dfs}(i-1,j),\textit{dfs}(i-1,(j-x)\bmod 3) + x)
$$
注意，如果 $(j-x)\bmod 3 < 0$，需要再 $+3$ 调整到 $[0,2]$ 内。考虑到这样写有些麻烦，不妨把 $j$ 的定义改为已选数字之和 $\bmod\ 3 = j$。（注意这里的定义是已经选的，上面定义的是还需要选的。）
这样修改后，不选 $x$ 仍然是 $\textit{dfs}(i,j) = \textit{dfs}(i-1,j)$；选 $x$ 就是 $\textit{dfs}(i,j) = \textit{dfs}(i-1,(j+x)\bmod 3)$ 了。
这两种情况取最大值，有
$$
\textit{dfs}(i,j) = \max(\textit{dfs}(i-1,j),\textit{dfs}(i-1,(j+x)\bmod 3) + x)
$$
递归边界：$\textit{dfs}(-1,0)=0,\textit{dfs}(-1,1)=-\infty,\textit{dfs}(-1,2)=-\infty$。我们需要保证所选数字之和是 $3$ 的倍数，否则不符合题目要求。注意，如果没有选任何数字，那么会递归到 $\textit{dfs}(-1,0)$，得到 $0$，这是符合题目要求的。
注：$-\infty$ 表示非法方案，这样后面取 $\max$ 的时候会自动排除非法方案。
递归入口：$\textit{dfs}(n-1,0)$。
class Solution:
def maxSumDivThree(self, nums: List[int]) -> int:
@cache # 记忆化搜索
def dfs(i: int, j: int) -> int:
if i < 0: return -inf if j else 0
return max(dfs(i - 1, j), dfs(i - 1, (j + nums[i]) % 3) + nums[i])
return dfs(len(nums) - 1, 0)
class Solution {
public int maxSumDivThree(int[] nums) {
int n = nums.length;
int[][] memo = new int[n][3];
for (int i = 0; i < n; i++)
Arrays.fill(memo[i], -1); // -1 表示没有计算过
return dfs(memo, nums, n - 1, 0);
}
private int dfs(int[][] memo, int[] nums, int i, int j) {
if (i < 0) return j == 0 ? 0 : Integer.MIN_VALUE;
if (memo[i][j] != -1) return memo[i][j]; // 之前计算过
return memo[i][j] = Math.max(dfs(memo, nums, i - 1, j),
dfs(memo, nums, i - 1, (j + nums[i]) % 3) + nums[i]);
}
}
class Solution {
public:
int maxSumDivThree(vector<int> &nums) {
int n = nums.size(), memo[n][3];
memset(memo, -1, sizeof(memo)); // -1 表示没有计算过
auto dfs = [&](auto&& dfs, int i, int j) -> int {
if (i < 0) return j ? INT_MIN : 0;
int &res = memo[i][j]; // 注意这里是引用，下面会直接修改 memo[i][j]
if (res != -1) return res; // 之前计算过
return res = max(dfs(dfs, i - 1, j), dfs(dfs, i - 1, (j + nums[i]) % 3) + nums[i]);
};
return dfs(dfs, n - 1, 0);
}
};
func maxSumDivThree(nums []int) int {
n := len(nums)
memo := make([][3]int, n)
for i := range memo {
for j := range memo[i] {
memo[i][j] = -1 // -1 表示没有计算过
}
}
var dfs func(int, int) int
dfs = func(i, j int) int {
if i < 0 {
if j == 0 {
return 0
}
return math.MinInt
}
p := &memo[i][j]
if *p != -1 { // 之前计算过
return *p
}
*p = max(dfs(i-1, j), dfs(i-1, (j+nums[i])%3)+nums[i])
return *p
}
return dfs(n-1, 0)
}
func max(a, b int) int { if a < b { return b }; return a }
我们可以去掉递归中的「递」，只保留「归」的部分，即自底向上计算。
做法：
具体来说，$f[i][j]$ 的含义与状态转移方程和 $\textit{dfs}(i,j)$ 的是一致的，即
$$
f[i][j] = \max(f[i-1][j],f[i-1][(j+x)\bmod 3] + x)
$$
但当 $i=0$ 时，等号右边会出现负数下标。或者说，这种定义方式没有状态能表示递归边界。
解决办法：在 $f$ 数组的上边加一排，把原来的 $f[i]$ 改成 $f[i+1]$，$f[i-1]$ 改成 $f[i]$。此时 $f[0][j]$ 就对应着 $\textit{dfs}(-1,j)$。
修改后的递推式为
$$
f[i+1][j] = \max(f[i][j],f[i][(j+x)\bmod 3] + x)
$$
初始值 $f[0]=[0,-\infty,-\infty]$，翻译自 $\textit{dfs}(-1,0)=0,\textit{dfs}(-1,1)=-\infty,\textit{dfs}(-1,2)=-\infty$。
答案为 $f[n][0]$，翻译自 $\textit{dfs}(n-1,0)$。
class Solution:
def maxSumDivThree(self, nums: List[int]) -> int:
f = [[-inf] * 3 for _ in range(len(nums) + 1)]
f[0][0] = 0
for i, x in enumerate(nums):
for j in range(3):
f[i + 1][j] = max(f[i][j], f[i][(j + x) % 3] + x)
return f[-1][0]
class Solution {
public int maxSumDivThree(int[] nums) {
int n = nums.length;
var f = new int[n + 1][3];
f[0][1] = f[0][2] = Integer.MIN_VALUE;
for (int i = 0; i < n; i++)
for (int j = 0; j < 3; j++)
f[i + 1][j] = Math.max(f[i][j], f[i][(j + nums[i]) % 3] + nums[i]);
return f[n][0];
}
}
class Solution {
public:
int maxSumDivThree(vector<int> &nums) {
int n = nums.size(), f[n + 1][3];
f[0][0] = 0, f[0][1] = INT_MIN, f[0][2] = INT_MIN;
for (int i = 0; i < n; i++)
for (int j = 0; j < 3; j++)
f[i + 1][j] = max(f[i][j], f[i][(j + nums[i]) % 3] + nums[i]);
return f[n][0];
}
};
func maxSumDivThree(nums []int) int {
n := len(nums)
f := make([][3]int, n+1)
f[0][1] = math.MinInt
f[0][2] = math.MinInt
for i, x := range nums {
for j := 0; j < 3; j++ {
f[i+1][j] = max(f[i][j], f[i][(j+x)%3]+x)
}
}
return f[n][0]
}
func max(a, b int) int { if a < b { return b }; return a }
由于 $f[i+1]$ 只依赖 $f[i]$，那么 $f[i-1]$ 及其之前的数据就没用了。
例如计算 $f[2]$ 的时候，数组 $f[0]$ 不再使用了。
那么干脆把 $f[2]$ 填到 $f[0]$ 中。同理，把 $f[3]$ 填到 $f[1]$ 中，$f[4]$ 填到 $f[0]$ 中，……
因此可以只用两个长为 $n+1$ 的数组滚动计算。
具体可以看【基础算法精讲 18】中的画图讲解。
class Solution:
def maxSumDivThree(self, nums: List[int]) -> int:
f = [[-inf] * 3 for _ in range(2)]
f[0][0] = 0
for i, x in enumerate(nums):
for j in range(3):
f[(i + 1) % 2][j] = max(f[i % 2][j], f[i % 2][(j + x) % 3] + x)
return f[len(nums) % 2][0]
class Solution {
public int maxSumDivThree(int[] nums) {
int n = nums.length;
var f = new int[2][3];
f[0][1] = f[0][2] = Integer.MIN_VALUE;
for (int i = 0; i < n; i++)
for (int j = 0; j < 3; j++)
f[(i + 1) % 2][j] = Math.max(f[i % 2][j], f[i % 2][(j + nums[i]) % 3] + nums[i]);
return f[n % 2][0];
}
}
class Solution {
public:
int maxSumDivThree(vector<int> &nums) {
int n = nums.size(), f[2][3];
f[0][0] = 0, f[0][1] = INT_MIN, f[0][2] = INT_MIN;
for (int i = 0; i < n; i++)
for (int j = 0; j < 3; j++)
f[(i + 1) % 2][j] = max(f[i % 2][j], f[i % 2][(j + nums[i]) % 3] + nums[i]);
return f[n % 2][0];
}
};
func maxSumDivThree(nums []int) int {
f := [2][3]int{{0, math.MinInt, math.MinInt}}
for i, x := range nums {
for j := 0; j < 3; j++ {
f[(i+1)%2][j] = max(f[i%2][j], f[i%2][(j+x)%3]+x)
}
}
return f[len(nums)%2][0]
}
func max(a, b int) int { if a < b { return b }; return a }
相比贪心算法，动态规划的适用性更广。请你思考，如果数组中有负数，动态规划是否也能得到正确的结果？如果把 $3$ 换成其它数字呢？欢迎在评论区发表你的看法。
欢迎关注 B站@灵茶山艾府
remainder分别为余数0，1，2时的最大值
class Solution {
public:
int maxSumDivThree(vector<int>& nums) {
int N = nums.size();
int remainder[3] = {0};
for(int i = 0; i < N; i++){
int a,b,c;
a = remainder[0] + nums[i];
b = remainder[1] + nums[i];
c = remainder[2] + nums[i];
remainder[a%3] = max(remainder[a%3], a);
remainder[b%3] = max(remainder[b%3], b);
remainder[c%3] = max(remainder[c%3], c);
}
return remainder[0];
}
};
根据题意很容易想到用状态转移与动态规划的思路来解决
零状态：当前数字最大和模三余零一状态：当前数字最大和模三余一二状态：当前数字最大和模三余二对于任意一种状态，下一步我们都有两种选择，一是选择当前元素，二是不选择当前元素
dp[i][*] = max{dp[i-1][*],dp[i-1][*] + nums[i]} (* 取值为 0,1,2)
以上是常见的动态规划的递推结构
本题的状态转移显而易见，以当前状态是零状态为例。我们可以想到，前一个状态无非是零状态``一状态``二状态，三种情况，针对这三种情况我们分类讨论即可
显然可以直接两种方法直接结合起来
所以零状态如何转移我们理解了之后，可以一次写出一状态的转移，二状态的转移
LeetCode1262 可被三整除的最大和
LeetCode688 “马”在棋盘上的概率
LeetCode967 连续差相同的数字
LeetCode873 最长的斐波那契子序列的长度
LeetCode1218 最长定差子序列
LeetCode523 连续子数组和
LeetCode576 出界的路径数
LeetCode1220 统计元音字母序列的数目
###cpp
class Solution {
public:
int maxSumDivThree(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> dp(n + 1, vector<int>(3, 0));
dp[0][0] = 0; dp[0][1] = INT_MIN; dp[0][2] = INT_MIN;
for (int i = 1; i <= n; i++) {
if (nums[i - 1] % 3 == 0) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][0] + nums[i - 1]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][1] + nums[i - 1]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][2] + nums[i - 1]);
}
else if (nums[i - 1] % 3 == 1) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] + nums[i - 1]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + nums[i - 1]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + nums[i - 1]);
}
else if (nums[i - 1] % 3 == 2) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + nums[i - 1]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][2] + nums[i - 1]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][0] + nums[i - 1]);
}
}
return dp[n][0];
}
};
给你一个整数数组 nums 。一次操作中，你可以将 nums 中的 任意 一个元素增加或者减少 1 。
请你返回将 nums 中所有元素都可以被 3 整除的 最少 操作次数。
示例 1：
输入：nums = [1,2,3,4]
输出：3
解释：
通过以下 3 个操作，数组中的所有元素都可以被 3 整除：
示例 2：
输入：nums = [3,6,9]
输出：0
提示：
1 <= nums.length <= 501 <= nums[i] <= 50对于数组 $\textit{nums}$ 中的每个元素，可以根据元素除以 $3$ 的余数计算使元素可以被 $3$ 整除的最少操作次数。
如果一个元素除以 $3$ 的余数是 $0$，则不需要执行操作。
如果一个元素除以 $3$ 的余数是 $1$，则需要将元素减少 $1$ 才能使元素可以被 $3$ 整除，最少操作次数是 $1$。
如果一个元素除以 $3$ 的余数是 $2$，则需要将元素增加 $1$ 才能使元素可以被 $3$ 整除，最少操作次数是 $1$。
上述情况可以概括成两种情况。
能被 $3$ 整除的元素的最少操作次数是 $0$。
不能被 $3$ 整除的元素的最少操作次数是 $1$。
因此，使数组 $\textit{nums}$ 中所有元素都可以被 $3$ 整除的最少操作次数等于数组 $\textit{nums}$ 中的不能被 $3$ 整除的元素个数。
###Java
class Solution {
public int minimumOperations(int[] nums) {
int operations = 0;
for (int num : nums) {
if (num % 3 != 0) {
operations++;
}
}
return operations;
}
}
###C#
public class Solution {
public int MinimumOperations(int[] nums) {
int operations = 0;
foreach (int num in nums) {
if (num % 3 != 0) {
operations++;
}
}
return operations;
}
}
时间复杂度：$O(n)$，其中 $n$ 是数组 $\textit{nums}$ 的长度。需要遍历数组一次。
空间复杂度：$O(1)$。
考虑更一般的情形，对于正整数 $d$，计算使数组 $\textit{nums}$ 中所有元素都可以被 $d$ 整除的最少操作次数。
对于正整数元素 $\textit{num}$，当 $\textit{num} \bmod d = 0$ 时最少操作次数是 $0$，当 $\textit{num} \bmod d \ne 0$ 时可以将 $\textit{num}$ 减少或增加使更新后的 $\textit{num}$ 可以被 $d$ 整除。
将 $\textit{num}$ 减少到可以被 $d$ 整除，最少操作次数是 $\textit{num} \bmod d$。
将 $\textit{num}$ 增加到可以被 $d$ 整除，最少操作次数是 $d - \textit{num} \bmod d$。
为了使操作次数最少，应取两种情况中的最小值，因此使 $\textit{num}$ 可以被 $d$ 整除的最少操作次数是 $\min(\textit{num} \bmod d, d - \textit{num} \bmod d)$。
当 $\textit{num} \bmod d = 0$ 时，$\min(\textit{num} \bmod d, d - \textit{num} \bmod d) = 0$，最少操作次数也是 $\min(\textit{num} \bmod d, d - \textit{num} \bmod d)$。因此对于任意元素 $\textit{num}$，使 $\textit{num}$ 可以被 $d$ 整除的最少操作次数是 $\min(\textit{num} \bmod d, d - \textit{num} \bmod d)$。
遍历数组 $\textit{nums}$ 分别计算使每个元素可以被 $d$ 整除的最少操作次数之后，即可得到使数组 $\textit{nums}$ 中所有元素都可以被 $d$ 整除的最少操作次数。
###Java
class Solution {
static final int DIVISOR = 3;
public int minimumOperations(int[] nums) {
int operations = 0;
for (int num : nums) {
operations += Math.min(num % DIVISOR, DIVISOR - num % DIVISOR);
}
return operations;
}
}
###C#
public class Solution {
const int DIVISOR = 3;
public int MinimumOperations(int[] nums) {
int operations = 0;
foreach (int num in nums) {
operations += Math.Min(num % DIVISOR, DIVISOR - num % DIVISOR);
}
return operations;
}
}
时间复杂度：$O(n)$，其中 $n$ 是数组 $\textit{nums}$ 的长度。需要遍历数组一次。
空间复杂度：$O(1)$。
遍历 $\textit{nums}$，按照元素模 $3$ 的余数分类：
由此可见，对于不是 $3$ 的倍数的元素，只需操作一次就可以变成 $3$ 的倍数。
所以答案为不是 $3$ 的倍数的元素个数。
###py
class Solution:
def minimumOperations(self, nums: List[int]) -> int:
return sum(x % 3 != 0 for x in nums)
###java
class Solution {
public int minimumOperations(int[] nums) {
int ans = 0;
for (int x : nums) {
ans += x % 3 != 0 ? 1 : 0;
}
return ans;
}
}
###cpp
class Solution {
public:
int minimumOperations(vector<int>& nums) {
int ans = 0;
for (int x : nums) {
ans += x % 3 != 0;
}
return ans;
}
};
###c
int minimumOperations(int* nums, int numsSize) {
int ans = 0;
for (int i = 0; i < numsSize; i++) {
ans += nums[i] % 3 != 0;
}
return ans;
}
###go
func minimumOperations(nums []int) (ans int) {
for _, x := range nums {
if x%3 != 0 {
ans++
}
}
return
}
###js
var minimumOperations = function(nums) {
return _.sumBy(nums, x => (x % 3 !== 0 ? 1 : 0));
};
###rust
impl Solution {
pub fn minimum_operations(nums: Vec<i32>) -> i32 {
nums.into_iter().filter(|&x| x % 3 != 0).count() as _
}
}
把题目中的 $3$ 改成 $4$ 呢？改成 $m$ 呢？
请看 视频讲解，欢迎点赞关注！
欢迎关注 B站@灵茶山艾府
给你一个字符串 s ，返回 s 中 长度为 3 的不同回文子序列 的个数。
即便存在多种方法来构建相同的子序列，但相同的子序列只计数一次。
回文 是正着读和反着读一样的字符串。
子序列 是由原字符串删除其中部分字符（也可以不删除）且不改变剩余字符之间相对顺序形成的一个新字符串。
"ace" 是 "abcde" 的一个子序列。
示例 1：
输入：s = "aabca"
输出：3
解释：长度为 3 的 3 个回文子序列分别是：
- "aba" ("aabca" 的子序列)
- "aaa" ("aabca" 的子序列)
- "aca" ("aabca" 的子序列)
示例 2：
输入：s = "adc" 输出：0 解释："adc" 不存在长度为 3 的回文子序列。
示例 3：
输入：s = "bbcbaba"
输出：4
解释：长度为 3 的 4 个回文子序列分别是：
- "bbb" ("bbcbaba" 的子序列)
- "bcb" ("bbcbaba" 的子序列)
- "bab" ("bbcbaba" 的子序列)
- "aba" ("bbcbaba" 的子序列)
提示：
3 <= s.length <= 105s 仅由小写英文字母组成思路与算法
我们可以枚举回文序列两侧的字符种类。对于每种字符，如果它在字符串 $s$ 中出现，我们记录它第一次出现的下标 $l$ 与最后一次出现的下标 $r$。那么，以该字符为两侧的回文子序列，它中间的字符只可能在 $s[l+1..r-1]$ 中选取；且以该字符为两侧的回文子序列的种数即为 $s[l+1..r-1]$ 中的字符种数。
我们遍历 $s[l+1..r-1]$ 子串计算该子串中的字符种数。在遍历时，我们可以使用哈希集合来维护该子串中的字符种类；当遍历完成后，哈希集合内元素的数目即为该子串中的字符总数。
在枚举两侧字符种类时，我们维护这些回文子序列种数之和，并最终作为答案返回。
代码
###C++
class Solution {
public:
int countPalindromicSubsequence(string s) {
int n = s.size();
int res = 0;
// 枚举两侧字符
for (char ch = 'a'; ch <= 'z'; ++ch){
int l = 0, r = n - 1;
// 寻找该字符第一次出现的下标
while (l < n && s[l] != ch){
++l;
}
// 寻找该字符最后一次出现的下标
while (r >= 0 && s[r] != ch){
--r;
}
if (r - l < 2){
// 该字符未出现，或两下标中间的子串不存在
continue;
}
// 利用哈希集合统计 s[l+1..r-1] 子串的字符总数，并更新答案
unordered_set<char> charset;
for (int k = l + 1; k < r; ++k){
charset.insert(s[k]);
}
res += charset.size();
}
return res;
}
};
###Python
class Solution:
def countPalindromicSubsequence(self, s: str) -> int:
n = len(s)
res = 0
# 枚举两侧字符
for i in range(26):
l, r = 0, n - 1
# 寻找该字符第一次出现的下标
while l < n and ord(s[l]) - ord('a') != i:
l += 1
# 寻找该字符最后一次出现的下标
while r >= 0 and ord(s[r]) - ord('a') != i:
r -= 1
if r - l < 2:
# 该字符未出现，或两下标中间的子串不存在
continue
# 利用哈希集合统计 s[l+1..r-1] 子串的字符总数，并更新答案
charset = set()
for k in range(l + 1, r):
charset.add(s[k])
res += len(charset)
return res
###Java
class Solution {
public int countPalindromicSubsequence(String s) {
int n = s.length();
int res = 0;
// 枚举两侧字符
for (char ch = 'a'; ch <= 'z'; ++ch) {
int l = 0, r = n - 1;
// 寻找该字符第一次出现的下标
while (l < n && s.charAt(l) != ch) {
++l;
}
// 寻找该字符最后一次出现的下标
while (r >= 0 && s.charAt(r) != ch) {
--r;
}
if (r - l < 2) {
// 该字符未出现，或两下标中间的子串不存在
continue;
}
// 利用哈希集合统计 s[l+1..r-1] 子串的字符总数，并更新答案
Set<Character> charset = new HashSet<>();
for (int k = l + 1; k < r; ++k) {
charset.add(s.charAt(k));
}
res += charset.size();
}
return res;
}
}
###C#
public class Solution {
public int CountPalindromicSubsequence(string s) {
int n = s.Length;
int res = 0;
// 枚举两侧字符
for (char ch = 'a'; ch <= 'z'; ++ch) {
int l = 0, r = n - 1;
// 寻找该字符第一次出现的下标
while (l < n && s[l] != ch) {
++l;
}
// 寻找该字符最后一次出现的下标
while (r >= 0 && s[r] != ch) {
--r;
}
if (r - l < 2) {
// 该字符未出现，或两下标中间的子串不存在
continue;
}
// 利用哈希集合统计 s[l+1..r-1] 子串的字符总数，并更新答案
HashSet<char> charset = new HashSet<char>();
for (int k = l + 1; k < r; ++k) {
charset.Add(s[k]);
}
res += charset.Count;
}
return res;
}
}
###Go
func countPalindromicSubsequence(s string) int {
n := len(s)
res := 0
// 枚举两侧字符
for ch := 'a'; ch <= 'z'; ch++ {
l, r := 0, n-1
// 寻找该字符第一次出现的下标
for l < n && rune(s[l]) != ch {
l++
}
// 寻找该字符最后一次出现的下标
for r >= 0 && rune(s[r]) != ch {
r--
}
if r-l < 2 {
// 该字符未出现，或两下标中间的子串不存在
continue
}
// 利用哈希集合统计 s[l+1..r-1] 子串的字符总数，并更新答案
charset := make(map[rune]bool)
for _, c := range s[l+1:r] {
charset[c] = true
}
res += len(charset)
}
return res
}
###C
int countPalindromicSubsequence(char* s) {
int n = strlen(s);
int res = 0;
// 枚举两侧字符
for (char ch = 'a'; ch <= 'z'; ++ch) {
int l = 0, r = n - 1;
// 寻找该字符第一次出现的下标
while (l < n && s[l] != ch) {
++l;
}
// 寻找该字符最后一次出现的下标
while (r >= 0 && s[r] != ch) {
--r;
}
if (r - l < 2) {
// 该字符未出现，或两下标中间的子串不存在
continue;
}
// 利用哈希集合统计 s[l+1..r-1] 子串的字符总数，并更新答案
bool charset[26] = {false};
for (int k = l + 1; k < r; ++k) {
charset[s[k] - 'a'] = true;
}
int count = 0;
for (int i = 0; i < 26; ++i) {
if (charset[i]) {
count++;
}
}
res += count;
}
return res;
}
###JavaScript
var countPalindromicSubsequence = function(s) {
const n = s.length;
let res = 0;
// 枚举两侧字符
for (let ch = 'a'.charCodeAt(0); ch <= 'z'.charCodeAt(0); ch++) {
const c = String.fromCharCode(ch);
let l = 0, r = n - 1;
// 寻找该字符第一次出现的下标
while (l < n && s[l] !== c) {
++l;
}
// 寻找该字符最后一次出现的下标
while (r >= 0 && s[r] !== c) {
--r;
}
if (r - l < 2) {
// 该字符未出现，或两下标中间的子串不存在
continue;
}
// 利用哈希集合统计 s[l+1..r-1] 子串的字符总数，并更新答案
const charset = new Set();
for (let k = l + 1; k < r; k++) {
charset.add(s[k]);
}
res += charset.size;
}
return res;
};
###TypeScript
function countPalindromicSubsequence(s: string): number {
const n = s.length;
let res = 0;
// 枚举两侧字符
for (let ch = 'a'.charCodeAt(0); ch <= 'z'.charCodeAt(0); ch++) {
const c = String.fromCharCode(ch);
let l = 0, r = n - 1;
// 寻找该字符第一次出现的下标
while (l < n && s[l] !== c) {
++l;
}
// 寻找该字符最后一次出现的下标
while (r >= 0 && s[r] !== c) {
--r;
}
if (r - l < 2) {
// 该字符未出现，或两下标中间的子串不存在
continue;
}
// 利用哈希集合统计 s[l+1..r-1] 子串的字符总数，并更新答案
const charset = new Set<string>();
for (let k = l + 1; k < r; k++) {
charset.add(s[k]);
}
res += charset.size;
}
return res;
}
###Rust
use std::collections::HashSet;
impl Solution {
pub fn count_palindromic_subsequence(s: String) -> i32 {
let mut res = 0;
// 枚举两侧字符
for ch in 'a'..='z' {
// 使用迭代器找到第一个和最后一个出现位置
let mut chars = s.chars();
let l = chars.position(|c| c == ch);
let r = chars.rev().position(|c| c == ch).map(|pos| s.len() - 1 - pos);
if let (Some(l), Some(r)) = (l, r) {
if r > l + 1 {
// 收集中间字符
let unique_chars: HashSet<_> = s[l+1..r].chars().collect();
res += unique_chars.len() as i32;
}
}
}
res
}
}
复杂度分析
时间复杂度：$O(n|\Sigma| + |\Sigma|^2)$，其中 $n$ 为 $s$ 的长度，$|\Sigma|$ 为字符集的大小。我们总共需要枚举 $|\Sigma|$ 种字符，每次枚举至多需要遍历一次字符串 $s$ 与哈希集合，时间复杂度分别为 $O(n)$ 与 $O(|\Sigma|)$。
空间复杂度：$O(|\Sigma|)$，即为哈希集合的空间开销。
思路与算法
我们也可以遍历字符串 $s$ 枚举回文子序列中间的字符。假设 $s$ 的长度为 $n$，当我们遍历到 $s[i]$ 时，以 $s[i]$ 为中间字符的回文子序列种数即为前缀 $s[0..i-1]$ 与后缀 $s[i+1..n-1]$ 的公共字符种数。
对于一个任意的子串，由于其仅由小写英文字母组成，我们可以用一个 $32$ 位整数来表示该子串含有哪些字符。如果该整数从低到高第 $i$ 个二进制位为 $1$，那么代表该子串含有字典序为 $i$ 的小写英文字母。在遍历该子串时，我们需要用按位或来维护该整数。
为了简化计算，我们可以参照前文所述的对应关系，用两个 $32$ 位整数的数组 $\textit{pre}, \textit{suf}$ 分别维护 $s$ 中前缀与后缀包含的字符。其中，$\textit{pre}[i]$ 代表前缀 $s[0..i-1]$ 包含的字符种类，$\textit{suf}[i]$ 代表后缀 $s[i+1..n-1]$ 包含的字符种类。那么，以 $s[i]$ 为中间字符的回文子序列中，两侧字符的种类对应的状态即为 $\textit{pre}[i] & \textit{suf}[i]$，其中 $&$ 为按位与运算符。
为了避免重复计算，我们需要在遍历的同时使用按位或来维护每种字符为中间字符的回文子序列种数。最终，我们将不同种类字符对应的回文子序列总数求和作为答案返回。
代码
###C++
class Solution {
public:
int countPalindromicSubsequence(string s) {
int n = s.size();
int res = 0;
// 前缀/后缀字符状态数组
vector<int> pre(n), suf(n);
for (int i = 0; i < n; ++i) {
// 前缀 s[0..i-1] 包含的字符种类
pre[i] = (i ? pre[i - 1] : 0) | (1 << (s[i] - 'a'));
}
for (int i = n - 1; i >= 0; --i) {
// 后缀 s[i+1..n-1] 包含的字符种类
suf[i] = (i != n - 1 ? suf[i + 1] : 0) | (1 << (s[i] - 'a'));
}
// 每种中间字符的回文子序列状态数组
vector<int> ans(26);
for (int i = 1; i < n - 1; ++i) {
ans[s[i]-'a'] |= (pre[i - 1] & suf[i + 1]);
}
// 更新答案
for (int i = 0; i < 26; ++i) {
res += __builtin_popcount(ans[i]);
}
return res;
}
};
###Python
class Solution:
def countPalindromicSubsequence(self, s: str) -> int:
n = len(s)
res = 0
# 前缀/后缀字符状态数组
pre = [0] * n
suf = [0] * n
for i in range(n):
# 前缀 s[0..i-1] 包含的字符种类
pre[i] = (pre[i - 1] if i else 0) | (1 << (ord(s[i]) - ord('a')))
for i in range(n - 1, -1, -1):
# 后缀 s[i+1..n-1] 包含的字符种类
suf[i] = (suf[i + 1] if i != n - 1 else 0) | (1 << (ord(s[i]) - ord('a')))
# 每种中间字符的回文子序列状态数组
ans = [0] * 26
for i in range(1, n - 1):
ans[ord(s[i]) - ord('a')] |= pre[i - 1] & suf[i + 1]
# 更新答案
for i in range(26):
res += bin(ans[i]).count("1")
return res
###Java
class Solution {
public int countPalindromicSubsequence(String s) {
int n = s.length();
int res = 0;
// 前缀/后缀字符状态数组
int[] pre = new int[n];
int[] suf = new int[n];
for (int i = 0; i < n; ++i) {
// 前缀 s[0..i-1] 包含的字符种类
pre[i] = (i > 0 ? pre[i - 1] : 0) | (1 << (s.charAt(i) - 'a'));
}
for (int i = n - 1; i >= 0; --i) {
// 后缀 s[i+1..n-1] 包含的字符种类
suf[i] = (i != n - 1 ? suf[i + 1] : 0) | (1 << (s.charAt(i) - 'a'));
}
// 每种中间字符的回文子序列状态数组
int[] ans = new int[26];
for (int i = 1; i < n - 1; ++i) {
ans[s.charAt(i) - 'a'] |= (pre[i - 1] & suf[i + 1]);
}
// 更新答案
for (int i = 0; i < 26; ++i) {
res += Integer.bitCount(ans[i]);
}
return res;
}
}
###C#
public class Solution {
public int CountPalindromicSubsequence(string s) {
int n = s.Length;
int res = 0;
// 前缀/后缀字符状态数组
int[] pre = new int[n];
int[] suf = new int[n];
for (int i = 0; i < n; ++i) {
// 前缀 s[0..i-1] 包含的字符种类
pre[i] = (i > 0 ? pre[i - 1] : 0) | (1 << (s[i] - 'a'));
}
for (int i = n - 1; i >= 0; --i) {
// 后缀 s[i+1..n-1] 包含的字符种类
suf[i] = (i != n - 1 ? suf[i + 1] : 0) | (1 << (s[i] - 'a'));
}
// 每种中间字符的回文子序列状态数组
int[] ans = new int[26];
for (int i = 1; i < n - 1; ++i) {
ans[s[i] - 'a'] |= (pre[i - 1] & suf[i + 1]);
}
// 更新答案
for (int i = 0; i < 26; ++i) {
res += BitOperations.PopCount((uint)ans[i]);
}
return res;
}
}
###Go
func countPalindromicSubsequence(s string) int {
n := len(s)
res := 0
// 前缀/后缀字符状态数组
pre := make([]int, n)
suf := make([]int, n)
for i := 0; i < n; i++ {
// 前缀 s[0..i-1] 包含的字符种类
if i > 0 {
pre[i] = pre[i-1]
}
pre[i] |= 1 << (s[i] - 'a')
}
for i := n - 1; i >= 0; i-- {
// 后缀 s[i+1..n-1] 包含的字符种类
if i != n - 1 {
suf[i] = suf[i + 1]
}
suf[i] |= 1 << (s[i] - 'a')
}
// 每种中间字符的回文子序列状态数组
ans := make([]int, 26)
for i := 1; i < n - 1; i++ {
ans[s[i] - 'a'] |= (pre[i - 1] & suf[i + 1])
}
// 更新答案
for i := 0; i < 26; i++ {
res += bits.OnesCount(uint(ans[i]))
}
return res
}
###C
int countPalindromicSubsequence(char* s) {
int n = strlen(s);
int res = 0;
// 前缀/后缀字符状态数组
int pre[n], suf[n];
for (int i = 0; i < n; ++i) {
// 前缀 s[0..i-1] 包含的字符种类
pre[i] = (i ? pre[i - 1] : 0) | (1 << (s[i] - 'a'));
}
for (int i = n - 1; i >= 0; --i) {
// 后缀 s[i+1..n-1] 包含的字符种类
suf[i] = (i != n - 1 ? suf[i + 1] : 0) | (1 << (s[i] - 'a'));
}
// 每种中间字符的回文子序列状态数组
int ans[26] = {0};
for (int i = 1; i < n - 1; ++i) {
ans[s[i] - 'a'] |= (pre[i - 1] & suf[i + 1]);
}
// 更新答案
for (int i = 0; i < 26; ++i) {
res += __builtin_popcount(ans[i]);
}
return res;
}
###JavaScript
var countPalindromicSubsequence = function(s) {
const n = s.length;
let res = 0;
// 前缀/后缀字符状态数组
const pre = new Array(n).fill(0);
const suf = new Array(n).fill(0);
for (let i = 0; i < n; ++i) {
// 前缀 s[0..i-1] 包含的字符种类
pre[i] = (i > 0 ? pre[i - 1] : 0) | (1 << (s.charCodeAt(i) - 97));
}
for (let i = n - 1; i >= 0; --i) {
// 后缀 s[i+1..n-1] 包含的字符种类
suf[i] = (i !== n - 1 ? suf[i + 1] : 0) | (1 << (s.charCodeAt(i) - 97));
}
// 每种中间字符的回文子序列状态数组
const ans = new Array(26).fill(0);
for (let i = 1; i < n - 1; ++i) {
ans[s.charCodeAt(i) - 97] |= (pre[i-1] & suf[i + 1]);
}
// 更新答案
for (let i = 0; i < 26; ++i) {
res += ans[i].toString(2).split('1').length - 1;
}
return res;
};
###TypeScript
function countPalindromicSubsequence(s: string): number {
const n = s.length;
let res = 0;
// 前缀/后缀字符状态数组
const pre: number[] = new Array(n).fill(0);
const suf: number[] = new Array(n).fill(0);
for (let i = 0; i < n; ++i) {
// 前缀 s[0..i-1] 包含的字符种类
pre[i] = (i > 0 ? pre[i - 1] : 0) | (1 << (s.charCodeAt(i) - 97));
}
for (let i = n - 1; i >= 0; --i) {
// 后缀 s[i+1..n-1] 包含的字符种类
suf[i] = (i !== n - 1 ? suf[i + 1] : 0) | (1 << (s.charCodeAt(i) - 97));
}
// 每种中间字符的回文子序列状态数组
const ans: number[] = new Array(26).fill(0);
for (let i = 1; i < n - 1; ++i) {
ans[s.charCodeAt(i) - 97] |= (pre[i - 1] & suf[i + 1]);
}
// 更新答案
for (let i = 0; i < 26; ++i) {
res += ans[i].toString(2).split('1').length - 1;
}
return res;
}
###Rust
impl Solution {
pub fn count_palindromic_subsequence(s: String) -> i32 {
let n = s.len();
let mut res = 0;
// 前缀/后缀字符状态数组
let mut pre = vec![0u32; n];
let mut suf = vec![0u32; n];
for (i, c) in s.chars().enumerate() {
// 前缀 s[0..i-1] 包含的字符种类
pre[i] = if i > 0 { pre[i-1] } else { 0 } | (1 << (c as u8 - b'a'));
}
for (i, c) in s.chars().rev().enumerate() {
let i = n - 1 - i;
// 后缀 s[i+1..n-1] 包含的字符种类
suf[i] = if i != n - 1 { suf[i+1] } else { 0 } | (1 << (c as u8 - b'a'));
}
// 每种中间字符的回文子序列状态数组
let mut ans = vec![0u32; 26];
for (i, c) in s.chars().enumerate() {
if i > 0 && i < n - 1 {
ans[(c as u8 - b'a') as usize] |= pre[i-1] & suf[i+1];
}
}
// 更新答案
for &count in &ans {
res += count.count_ones() as i32;
}
res
}
}
复杂度分析
时间复杂度：$O(n + |\Sigma|)$，其中 $n$ 为 $s$ 的长度，$|\Sigma|$ 为字符集的大小。预处理前后缀状态数组与遍历 $s$ 更新每种字符状态数组的时间复杂度均为 $O(n)$，初始化每种字符状态数组与更新答案的时间复杂度均为 $O(|\Sigma|)$。
空间复杂度：$O(|\Sigma|)$，即为每种字符状态数组的空间开销。
###cpp
class Solution {
public:
int countPalindromicSubsequence(string s) {
//找到一前一后
map<char, int> first;
map<char, int> last;
int size = s.size();
for (int i = 0; i < size; ++i){
if (first.count(s[i])){
last[s[i]] = i;
}else{
first[s[i]] = i;
}
}
int res = 0;
for (char i = 'a'; i < 'a' + 26; i++){
if (!first.count(i) || !last.count(i)) continue;
int tL = first[i], tR = last[i];
vector<int> count(26);
for (int j = tL + 1; j < tR; ++j){
count[s[j] - 'a'] = 1;
}
for (int j = 0; j < 26; ++j){
if(count[j] == 1) res++;
}
}
return res;
}
};
本题要找长为 $3$ 的回文子序列，这要求子序列的第一个字母等于第三个字母。
换句话说，确定了子序列的前两个字母，就确定了子序列。
这引出了两类做法：
枚举子序列的第一、三个字母是 $\texttt{a},\texttt{b},\ldots,\texttt{z}$。
如果第一、三个字母都是 $\texttt{a}$，如何找到尽量多的不同的子序列？
例如 $s = \texttt{abbacad}$。如果选前两个 $\texttt{a}$ 作为子序列的第一、三个字母，我们只能找到子序列 $\texttt{aba}$。而如果选第一个 $\texttt{a}$ 和最后一个 $\texttt{a}$，夹在两个 $\texttt{a}$ 之间的字母都可以是子序列的第二个字母，从而找到第一、三个字母都是 $\texttt{a}$ 的所有子序列，即 $\texttt{aaa}$、$\texttt{aba}$ 和 $\texttt{aca}$。
算法：
class Solution:
def countPalindromicSubsequence(self, s: str) -> int:
ans = 0
for alpha in ascii_lowercase: # 枚举两侧字母 alpha
i = s.find(alpha) # 最左边的 alpha 的下标
if i < 0: # s 中没有 alpha
continue
j = s.rfind(alpha) # 最右边的 alpha 的下标
ans += len(set(s[i + 1: j])) # 统计有多少个不同的中间字母
return ans
class Solution {
public int countPalindromicSubsequence(String s) {
int ans = 0;
for (char alpha = 'a'; alpha <= 'z'; alpha++) { // 枚举两侧字母 alpha
int i = s.indexOf(alpha); // 最左边的 alpha 的下标
if (i < 0) { // s 中没有 alpha
continue;
}
int j = s.lastIndexOf(alpha); // 最右边的 alpha 的下标
boolean[] has = new boolean[26];
for (int k = i + 1; k < j; k++) { // 枚举中间字母 mid
int mid = s.charAt(k) - 'a';
if (!has[mid]) {
has[mid] = true; // 避免重复统计
ans++;
}
}
}
return ans;
}
}
class Solution {
public:
int countPalindromicSubsequence(string s) {
int ans = 0;
for (char alpha = 'a'; alpha <= 'z'; alpha++) { // 枚举两侧字母 alpha
int i = s.find(alpha); // 最左边的 alpha 的下标
if (i == string::npos) { // s 中没有 alpha
continue;
}
int j = s.rfind(alpha); // 最右边的 alpha 的下标
bool has[26]{};
for (int k = i + 1; k < j; k++) { // 枚举中间字母 s[k]
if (!has[s[k] - 'a']) {
has[s[k] - 'a'] = true; // 避免重复统计
ans++;
}
}
}
return ans;
}
};
int countPalindromicSubsequence(char* s) {
int ans = 0;
for (char alpha = 'a'; alpha <= 'z'; alpha++) { // 枚举两侧字母 alpha
char* p = strchr(s, alpha); // 找最左边的 alpha
if (p == NULL) { // s 中没有 alpha
continue;
}
int i = p - s; // 最左边的 alpha 的下标
int j = strrchr(s, alpha) - s; // 最右边的 alpha 的下标
bool has[26] = {};
for (int k = i + 1; k < j; k++) { // 枚举中间字母 s[k]
if (!has[s[k] - 'a']) {
has[s[k] - 'a'] = true; // 避免重复统计
ans++;
}
}
}
return ans;
}
func countPalindromicSubsequence(s string) (ans int) {
for alpha := byte('a'); alpha <= 'z'; alpha++ { // 枚举两侧字母 alpha
i := strings.IndexByte(s, alpha) // 最左边的 alpha 的下标
if i < 0 { // s 中没有 alpha
continue
}
j := strings.LastIndexByte(s, alpha) // 最右边的 alpha 的下标
if i+1 >= j { // 长度不足 3
continue
}
has := [26]bool{}
for _, mid := range s[i+1 : j] { // 枚举中间字母 mid
if !has[mid-'a'] {
has[mid-'a'] = true // 避免重复统计
ans++
}
}
}
return
}
var countPalindromicSubsequence = function(s) {
const ordA = 'a'.charCodeAt(0);
let ans = 0;
for (let alpha = ordA; alpha <= 'z'.charCodeAt(0); alpha++) { // 枚举两侧字母 alpha
const ch = String.fromCharCode(alpha);
const i = s.indexOf(ch); // 最左边的 alpha 的下标
if (i < 0) { // s 中没有 alpha
continue;
}
const j = s.lastIndexOf(ch); // 最右边的 alpha 的下标
const has = Array(26).fill(false);
for (let k = i + 1; k < j; k++) { // 枚举中间字母 mid
const mid = s.charCodeAt(k) - ordA;
if (!has[mid]) {
has[mid] = true; // 避免重复统计
ans++;
}
}
}
return ans;
};
impl Solution {
pub fn count_palindromic_subsequence(s: String) -> i32 {
let s = s.as_bytes();
let mut ans = 0;
for alpha in b'a'..=b'z' { // 枚举两侧字母 alpha
let i = s.iter().position(|&c| c == alpha); // 找最左边的 alpha
if i.is_none() { // s 中没有 alpha
continue;
}
let i = i.unwrap(); // 最左边的 alpha 的下标
let j = s.iter().rposition(|&c| c == alpha).unwrap(); // 最右边的 alpha 的下标
let mut has = [false; 26];
for k in i + 1..j { // 枚举中间字母 mid
let mid = (s[k] - b'a') as usize;
if !has[mid] {
has[mid] = true; // 避免重复统计
ans += 1;
}
}
}
ans
}
}
枚举 $i=1,2,\ldots,n-2$，把 $s[i]$ 当作子序列的第二个字母，那么对于第一、三个字母 $\alpha = \texttt{a},\texttt{b},\ldots,\texttt{z}$，我们需要判断：
暴力找是 $\mathcal{O}(n)$ 的，如何加速？
我们可以先遍历 $s$，统计 $s$ 中每个字母的个数，然后再从左到右遍历 $s$，把 $s[i]$ 的个数减一，就得到了后缀 $[i+1,n-1]$ 每个字母的个数。
对于前缀 $[0,i-1]$，在从左到右遍历 $s$ 的同时，记录遇到了哪些字母。
class Solution:
def countPalindromicSubsequence(self, s: str) -> int:
suf_cnt = Counter(s[1:]) # 统计 [1,n-1] 每个字母的个数
pre_set = set()
st = set()
for i in range(1, len(s) - 1): # 枚举中间字母 mid
mid = s[i]
suf_cnt[mid] -= 1 # 撤销 mid 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
if suf_cnt[mid] == 0: # 后缀 [i+1,n-1] 不包含 mid
del suf_cnt[mid] # 从 suf_cnt 中去掉 mid
pre_set.add(s[i - 1]) # 记录前缀 [0,i-1] 有哪些字母
for alpha in pre_set & suf_cnt.keys(): # mid 的左右两侧都有字母 alpha
st.add(alpha + mid)
return len(st)
class Solution {
public int countPalindromicSubsequence(String S) {
char[] s = S.toCharArray();
int n = s.length;
// 统计 [1,n-1] 每个字母的个数
int[] sufCnt = new int[26];
for (int i = 1; i < n; i++) {
sufCnt[s[i] - 'a']++;
}
boolean[] preHas = new boolean[26];
boolean[][] has = new boolean[26][26];
int ans = 0;
for (int i = 1; i < n - 1; i++) { // 枚举中间字母 mid
int mid = s[i] - 'a';
sufCnt[mid]--; // 撤销 mid 的计数，sufCnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
preHas[s[i - 1] - 'a'] = true; // 记录前缀 [0,i-1] 有哪些字母
for (int alpha = 0; alpha < 26; alpha++) { // 枚举两侧字母 alpha
// 判断 mid 的左右两侧是否都有字母 alpha
if (preHas[alpha] && sufCnt[alpha] > 0 && !has[mid][alpha]) {
has[mid][alpha] = true;
ans++;
}
}
}
return ans;
}
}
class Solution {
public:
int countPalindromicSubsequence(string s) {
int n = s.size();
// 统计 [1,n-1] 每个字母的个数
int suf_cnt[26]{};
for (int i = 1; i < n; i++) {
suf_cnt[s[i] - 'a']++;
}
bool pre_has[26]{};
bool has[26][26]{};
int ans = 0;
for (int i = 1; i < n - 1; i++) { // 枚举中间字母 mid
int mid = s[i] - 'a';
suf_cnt[mid]--; // 撤销 mid 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
pre_has[s[i - 1] - 'a'] = true; // 记录前缀 [0,i-1] 有哪些字母
for (int alpha = 0; alpha < 26; alpha++) { // 枚举两侧字母 alpha
// 判断 mid 的左右两侧是否都有字母 alpha
if (pre_has[alpha] && suf_cnt[alpha] && !has[mid][alpha]) {
has[mid][alpha] = true;
ans++;
}
}
}
return ans;
}
};
int countPalindromicSubsequence(char* s) {
// 统计 [1,n-1] 每个字母的个数
int suf_cnt[26] = {};
for (int i = 1; s[i]; i++) {
suf_cnt[s[i] - 'a']++;
}
bool pre_has[26] = {};
bool has[26][26] = {};
int ans = 0;
for (int i = 1; s[i + 1]; i++) { // 枚举中间字母 mid
int mid = s[i] - 'a';
suf_cnt[mid]--; // 撤销 mid 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
pre_has[s[i - 1] - 'a'] = true; // 记录前缀 [0,i-1] 有哪些字母
for (int alpha = 0; alpha < 26; alpha++) { // 枚举两侧字母 alpha
// 判断 mid 的左右两侧是否都有字母 alpha
if (pre_has[alpha] && suf_cnt[alpha] && !has[mid][alpha]) {
has[mid][alpha] = true;
ans++;
}
}
}
return ans;
}
func countPalindromicSubsequence(s string) (ans int) {
// 统计 s[1:] 每个字母的个数
sufCnt := [26]int{}
for _, ch := range s[1:] {
sufCnt[ch-'a']++
}
preHas := [26]bool{}
has := [26][26]bool{}
for i := 1; i < len(s)-1; i++ { // 枚举中间字母 mid
mid := s[i] - 'a'
sufCnt[mid]-- // 撤销 mid 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
preHas[s[i-1]-'a'] = true // 记录前缀 [0,i-1] 有哪些字母
for alpha := range 26 { // 枚举两侧字母 alpha
// 判断 mid 的左右两侧是否都有字母 alpha
if preHas[alpha] && sufCnt[alpha] > 0 && !has[mid][alpha] {
has[mid][alpha] = true
ans++
}
}
}
return
}
var countPalindromicSubsequence = function(s) {
const n = s.length;
const ordA = 'a'.charCodeAt(0);
// 统计 [1,n-1] 每个字母的个数
const sufCnt = Array(26).fill(0);
for (let i = 1; i < n; i++) {
sufCnt[s.charCodeAt(i) - ordA]++;
}
const preHas = Array(26).fill(false);
const has = Array.from({ length: 26 }, () => Array(26).fill(false));
let ans = 0;
for (let i = 1; i < n - 1; i++) { // 枚举中间字母 mid
const mid = s.charCodeAt(i) - ordA;
sufCnt[mid]--; // 撤销 mid 的计数，sufCnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
preHas[s.charCodeAt(i - 1) - ordA] = true; // 记录前缀 [0,i-1] 有哪些字母
for (let alpha = 0; alpha < 26; alpha++) { // 枚举两侧字母 alpha
// 判断 mid 的左右两侧是否都有字母 alpha
if (preHas[alpha] && sufCnt[alpha] && !has[mid][alpha]) {
has[mid][alpha] = true;
ans++;
}
}
}
return ans;
};
impl Solution {
pub fn count_palindromic_subsequence(s: String) -> i32 {
let s = s.as_bytes();
let n = s.len();
// 统计 [1,n-1] 每个字母的个数
let mut suf_cnt = [0; 26];
for &ch in &s[1..] {
suf_cnt[(ch - b'a') as usize] += 1;
}
let mut pre_has = [false; 26];
let mut has = [[false; 26]; 26];
let mut ans = 0;
for i in 1..n - 1 { // 枚举中间字母 mid
let mid = (s[i] - b'a') as usize;
suf_cnt[mid] -= 1; // 撤销 s[i] 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
pre_has[(s[i - 1] - b'a') as usize] = true; // 记录前缀 [0,i-1] 有哪些字母
for alpha in 0..26 { // 枚举两侧字母 alpha
// 判断 mid 的左右两侧是否都有字母 alpha
if pre_has[alpha] && suf_cnt[alpha] > 0 && !has[mid][alpha] {
has[mid][alpha] = true;
ans += 1;
}
}
}
ans
}
}
我们可以把集合或者布尔数组压缩成一个二进制数，二进制数中的 $0$ 表示 $\texttt{false}$，$1$ 表示 $\texttt{true}$。原理请看 从集合论到位运算，常见位运算技巧分类总结！
用与运算可以 $\mathcal{O}(1)$ 求出 $\textit{pre}$ 和 $\textit{suf}$ 的交集。
class Solution:
def countPalindromicSubsequence(self, s: str) -> int:
n = len(s)
ord_a = ord('a')
# 统计 [1,n-1] 每个字母的个数
suf_cnt = [0] * 26
suf = 0
for ch in s[1:]:
ch = ord(ch) - ord_a
suf_cnt[ch] += 1
suf |= 1 << ch # 把 ch 记录到二进制数 suf 中，表示后缀有 ch
pre = 0
ans = [0] * 26 # ans[mid] = 由 alpha 组成的二进制数
for i in range(1, n - 1): # 枚举中间字母 mid
mid = ord(s[i]) - ord_a
suf_cnt[mid] -= 1 # 撤销 mid 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
if suf_cnt[mid] == 0: # 后缀 [i+1,n-1] 不包含 mid
suf ^= 1 << mid # 从 suf 中去掉 mid
pre |= 1 << (ord(s[i - 1]) - ord_a) # 把 s[i-1] 记录到二进制数 pre 中，表示前缀有 s[i-1]
ans[mid] |= pre & suf # 计算 pre 和 suf 的交集，|= 表示把交集中的字母加到 ans[mid] 中
return sum(mask.bit_count() for mask in ans) # mask 中的每个 1 对应着一个 alpha
class Solution {
public int countPalindromicSubsequence(String S) {
char[] s = S.toCharArray();
int n = s.length;
// 统计 [1,n-1] 每个字母的个数
int[] sufCnt = new int[26];
int suf = 0;
for (int i = 1; i < n; i++) {
int ch = s[i] - 'a';
sufCnt[ch]++;
suf |= 1 << ch; // 把 ch 记录到二进制数 suf 中，表示后缀有 ch
}
int pre = 0;
int[] has = new int[26]; // has[mid] = 由 alpha 组成的二进制数
for (int i = 1; i < n - 1; i++) { // 枚举中间字母 mid
int mid = s[i] - 'a';
sufCnt[mid]--; // 撤销 mid 的计数，sufCnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
if (sufCnt[mid] == 0) { // 后缀 [i+1,n-1] 不包含 mid
suf ^= 1 << mid; // 从 suf 中去掉 mid
}
pre |= 1 << (s[i - 1] - 'a'); // 把 s[i-1] 记录到二进制数 pre 中，表示前缀有 s[i-1]
has[mid] |= pre & suf; // 计算 pre 和 suf 的交集，|= 表示把交集中的字母加到 has[mid] 中
}
int ans = 0;
for (int mask : has) {
ans += Integer.bitCount(mask); // mask 中的每个 1 对应着一个 alpha
}
return ans;
}
}
class Solution {
public:
int countPalindromicSubsequence(string s) {
int n = s.size();
// 统计 [1,n-1] 每个字母的个数
int suf_cnt[26]{};
int suf = 0;
for (int i = 1; i < n; i++) {
int ch = s[i] - 'a';
suf_cnt[ch]++;
suf |= 1 << ch; // 把 ch 记录到二进制数 suf 中，表示后缀有 ch
}
int pre = 0;
int has[26]{}; // has[mid] = 由 alpha 组成的二进制数
for (int i = 1; i < n - 1; i++) { // 枚举中间字母 mid
int mid = s[i] - 'a';
suf_cnt[mid]--; // 撤销 mid 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
if (suf_cnt[mid] == 0) { // 后缀 [i+1,n-1] 不包含 mid
suf ^= 1 << mid; // 从 suf 中去掉 mid
}
pre |= 1 << (s[i - 1] - 'a'); // 把 s[i-1] 记录到二进制数 pre 中，表示前缀有 s[i-1]
has[mid] |= pre & suf; // 计算 pre 和 suf 的交集，|= 表示把交集中的字母加到 has[mid] 中
}
int ans = 0;
for (int mask : has) {
ans += popcount((uint32_t) mask); // mask 中的每个 1 对应着一个 alpha
}
return ans;
}
};
int countPalindromicSubsequence(char* s) {
int n = strlen(s);
// 统计 [1,n-1] 每个字母的个数
int suf_cnt[26] = {};
int suf = 0;
for (int i = 1; s[i]; i++) {
int ch = s[i] - 'a';
suf_cnt[ch]++;
suf |= 1 << ch; // 把 ch 记录到二进制数 suf 中，表示后缀有 ch
}
int pre = 0;
int has[26] = {}; // has[mid] = 由 alpha 组成的二进制数
for (int i = 1; s[i + 1]; i++) { // 枚举中间字母 mid
int mid = s[i] - 'a';
suf_cnt[mid]--; // 撤销 mid 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
if (suf_cnt[mid] == 0) { // 后缀 [i+1,n-1] 不包含 mid
suf ^= 1 << mid; // 从 suf 中去掉 mid
}
pre |= 1 << (s[i - 1] - 'a'); // 把 s[i-1] 记录到二进制数 pre 中，表示前缀有 s[i-1]
has[mid] |= pre & suf; // 计算 pre 和 suf 的交集，|= 表示把交集中的字母加到 has[mid] 中
}
int ans = 0;
for (int i = 0; i < 26; i++) {
ans += __builtin_popcount(has[i]); // has[i] 中的每个 1 对应着一个 alpha
}
return ans;
}
func countPalindromicSubsequence(s string) (ans int) {
// 统计 [1,n-1] 每个字母的个数
sufCnt := [26]int{}
suf := 0
for _, ch := range s[1:] {
ch -= 'a'
sufCnt[ch]++
suf |= 1 << ch // 把 ch 记录到二进制数 suf 中，表示后缀有 ch
}
pre := 0
has := [26]int{} // has[mid] = 由 alpha 组成的二进制数
for i := 1; i < len(s)-1; i++ { // 枚举中间字母 mid
mid := s[i] - 'a'
sufCnt[mid]-- // 撤销 mid 的计数，sufCnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
if sufCnt[mid] == 0 { // 后缀 [i+1,n-1] 不包含 mid
suf ^= 1 << mid // 从 suf 中去掉 mid
}
pre |= 1 << (s[i-1] - 'a') // 把 s[i-1] 记录到二进制数 pre 中，表示前缀有 s[i-1]
has[mid] |= pre & suf // 计算 pre 和 suf 的交集，|= 表示把交集中的字母加到 has[mid] 中
}
for _, mask := range has {
ans += bits.OnesCount(uint(mask)) // mask 中的每个 1 对应着一个 alpha
}
return
}
var countPalindromicSubsequence = function(s) {
const n = s.length;
const ordA = 'a'.charCodeAt(0);
// 统计 [1,n-1] 每个字母的个数
const sufCnt = Array(26).fill(0);
let suf = 0;
for (let i = 1; i < n; i++) {
const ch = s.charCodeAt(i) - ordA;
sufCnt[ch]++;
suf |= 1 << ch; // 把 ch 记录到二进制数 suf 中，表示后缀有 ch
}
let pre = 0;
const has = Array(26).fill(0); // has[mid] = 由 alpha 组成的二进制数
for (let i = 1; i < n - 1; i++) { // 枚举中间字母 mid
const mid = s.charCodeAt(i) - ordA;
sufCnt[mid]--; // 撤销 mid 的计数，sufCnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
if (sufCnt[mid] === 0) { // 后缀 [i+1,n-1] 不包含 mid
suf ^= 1 << mid; // 从 suf 中去掉 mid
}
pre |= 1 << (s.charCodeAt(i - 1) - ordA); // 把 s[i-1] 记录到二进制数 pre 中，表示前缀有 s[i-1]
has[mid] |= pre & suf; // 计算 pre 和 suf 的交集，|= 表示把交集中的字母加到 has[mid] 中
}
let ans = 0;
for (const mask of has) {
ans += bitCount32(mask); // mask 中的每个 1 对应着一个 alpha
}
return ans;
};
// 参考 Java 的 Integer.bitCount
function bitCount32(i) {
i = i - ((i >>> 1) & 0x55555555);
i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
i = (i + (i >>> 4)) & 0x0f0f0f0f;
i = i + (i >>> 8);
i = i + (i >>> 16);
return i & 0x3f;
}
impl Solution {
pub fn count_palindromic_subsequence(s: String) -> i32 {
let s = s.as_bytes();
let n = s.len();
// 统计 [1,n-1] 每个字母的个数
let mut suf_cnt = [0; 26];
let mut suf = 0;
for &ch in &s[1..] {
let ch = (ch - b'a') as usize;
suf_cnt[ch] += 1;
suf |= 1 << ch; // 把 ch 记录到二进制数 suf 中，表示后缀有 ch
}
let mut pre = 0;
let mut has = [0u32; 26]; // has[mid] = 由 alpha 组成的二进制数
for i in 1..n - 1 { // 枚举中间字母 mid
let mid = (s[i] - b'a') as usize;
suf_cnt[mid] -= 1; // 撤销 mid 的计数，suf_cnt 剩下的就是后缀 [i+1,n-1] 每个字母的个数
if suf_cnt[mid] == 0 { // 后缀 [i+1,n-1] 不包含 mid
suf ^= 1 << mid; // 从 suf 中去掉 mid
}
pre |= 1 << (s[i - 1] - b'a'); // 把 s[i-1] 记录到二进制数 pre 中，表示前缀有 s[i-1]
has[mid] |= pre & suf; // 计算 pre 和 suf 的交集，|= 表示把交集中的字母加到 has[mid] 中
}
// mask 中的每个 1 对应着一个 alpha
has.into_iter().map(|mask| mask.count_ones() as i32).sum()
}
}
欢迎关注 B站@灵茶山艾府
把 $2$ 改成 $k$ 怎么做？
更一般地，每个区间要包含的数字个数各有不同，怎么做？
这题是 2589. 完成所有任务的最少时间，我的题解。
class Solution:
def intersectionSizeTwo(self, intervals: List[List[int]]) -> int:
intervals.sort(key=lambda interval: interval[1])
# 栈中保存闭区间左右端点，栈底到栈顶的区间长度的和
st = [(-2, -2, 0)] # 哨兵，保证不和任何区间相交
for start, end in intervals:
_, r, s = st[bisect_left(st, (start,)) - 1]
d = 2 - (st[-1][2] - s) # 去掉运行中的时间点
if start <= r: # start 在区间 st[i] 内
d -= r - start + 1 # 去掉运行中的时间点
if d <= 0:
continue
while end - st[-1][1] <= d: # 剩余的 d 填充区间后缀
l, r, _ = st.pop()
d += r - l + 1 # 合并区间
st.append((end - d + 1, end, st[-1][2] + d))
return st[-1][2]
class Solution {
public int intersectionSizeTwo(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> a[1] - b[1]);
// 栈中保存闭区间左右端点，栈底到栈顶的区间长度的和
List<int[]> st = new ArrayList<>();
st.add(new int[]{-2, -2, 0}); // 哨兵，保证不和任何区间相交
for (int[] t : intervals) {
int start = t[0], end = t[1];
int[] e = st.get(lowerBound(st, start) - 1);
int d = 2 - (st.get(st.size() - 1)[2] - e[2]); // 去掉运行中的时间点
if (start <= e[1]) { // start 在区间 st[i] 内
d -= e[1] - start + 1; // 去掉运行中的时间点
}
if (d <= 0) {
continue;
}
while (end - st.get(st.size() - 1)[1] <= d) { // 剩余的 d 填充区间后缀
e = st.remove(st.size() - 1);
d += e[1] - e[0] + 1; // 合并区间
}
st.add(new int[]{end - d + 1, end, st.get(st.size() - 1)[2] + d});
}
return st.get(st.size() - 1)[2];
}
// 开区间二分
// 见 https://www.bilibili.com/video/BV1AP41137w7/
private int lowerBound(List<int[]> st, int target) {
int left = -1, right = st.size(); // 开区间 (left, right)
while (left + 1 < right) { // 区间不为空
// 循环不变量：
// st[left] < target
// st[right] >= target
int mid = (left + right) >>> 1;
if (st.get(mid)[0] < target) {
left = mid; // 范围缩小到 (mid, right)
} else {
right = mid; // 范围缩小到 (left, mid)
}
}
return right;
}
}
class Solution {
public:
int intersectionSizeTwo(vector<vector<int>>& intervals) {
ranges::sort(intervals, {}, [](auto& a) { return a[1]; });
// 栈中保存闭区间左右端点，栈底到栈顶的区间长度的和
vector<array<int, 3>> st = {{-2, -2, 0}}; // 哨兵，保证不和任何区间相交
for (auto& t : intervals) {
int start = t[0], end = t[1];
auto [_, r, s] = *--ranges::lower_bound(st, start, {}, [](auto& x) { return x[0]; });
int d = 2 - (st.back()[2] - s); // 去掉运行中的时间点
if (start <= r) { // start 在区间 st[i] 内
d -= r - start + 1; // 去掉运行中的时间点
}
if (d <= 0) {
continue;
}
while (end - st.back()[1] <= d) { // 剩余的 d 填充区间后缀
auto [l, r, _] = st.back();
st.pop_back();
d += r - l + 1; // 合并区间
}
st.push_back({end - d + 1, end, st.back()[2] + d});
}
return st.back()[2];
}
};
func intersectionSizeTwo(intervals [][]int) int {
slices.SortFunc(intervals, func(a, b []int) int { return a[1] - b[1] })
// 栈中保存闭区间左右端点，栈底到栈顶的区间长度的和
type tuple struct{ l, r, s int }
st := []tuple{{-2, -2, 0}} // 哨兵，保证不和任何区间相交
for _, p := range intervals {
start, end := p[0], p[1]
i := sort.Search(len(st), func(i int) bool { return st[i].l >= start }) - 1
d := 2 - (st[len(st)-1].s - st[i].s) // 去掉运行中的时间点
if start <= st[i].r { // start 在区间 st[i] 内
d -= st[i].r - start + 1 // 去掉运行中的时间点
}
if d <= 0 {
continue
}
for end-st[len(st)-1].r <= d { // 剩余的 d 填充区间后缀
top := st[len(st)-1]
st = st[:len(st)-1]
d += top.r - top.l + 1 // 合并区间
}
st = append(st, tuple{end - d + 1, end, st[len(st)-1].s + d})
}
return st[len(st)-1].s
}
见下面贪心题单的「§2.3 区间选点」。
欢迎关注 B站@灵茶山艾府
给你一个二维整数数组 intervals ，其中 intervals[i] = [starti, endi] 表示从 starti 到 endi 的所有整数，包括 starti 和 endi 。
包含集合 是一个名为 nums 的数组，并满足 intervals 中的每个区间都 至少 有 两个 整数在 nums 中。
intervals = [[1,3], [3,7], [8,9]] ，那么 [1,2,4,7,8,9] 和 [2,3,4,8,9] 都符合 包含集合 的定义。返回包含集合可能的最小大小。
示例 1：
输入：intervals = [[1,3],[3,7],[8,9]] 输出：5 解释：nums = [2, 3, 4, 8, 9]. 可以证明不存在元素数量为 4 的包含集合。
示例 2：
输入：intervals = [[1,3],[1,4],[2,5],[3,5]] 输出：3 解释：nums = [2, 3, 4]. 可以证明不存在元素数量为 2 的包含集合。
示例 3：
输入：intervals = [[1,2],[2,3],[2,4],[4,5]] 输出：5 解释：nums = [1, 2, 3, 4, 5]. 可以证明不存在元素数量为 4 的包含集合。
提示：
1 <= intervals.length <= 3000intervals[i].length == 20 <= starti < endi <= 108不要被样例数据误导了，题目要我们求最小点集的数量，并不规定点集 S 是连续段。
为了方便，我们令 intervals 为 ins。
当只有一个线段时，我们可以在线段内取任意两点作为 S 成员，而当只有两个线段时，我们可以两个线段重合情况进行决策：
S 最小化的题意，我们可以先取重合点，然后再两个线段中各取一个；不难发现，当出现重合的所有情况中，必然可以归纳某个线段的边缘点上。即不存在两个线段存在重合点，仅发生在两线段的中间部分：
因此我们可以从边缘点决策进行入手。
具体的，我们可以按照「右端点从小到大，左端点从大到小」的双关键字排序，然后从前往后处理每个区间，处理过程中不断往 S 中添加元素，由于我们已对所有区间排序且从前往后处理，因此我们往 S 中增加元素的过程中必然是单调递增，同时在对新的后续区间考虑是否需要往 S 中添加元素来满足题意时，也是与 S 中的最大/次大值（点集中的边缘元素）做比较，因此我们可以使用两个变量 a 和 b 分别代指当前集合 S 中的次大值和最大值（a 和 b 初始化为足够小的值 $-1$），而无需将整个 S 存下来。
不失一般性的考虑，当我们处理到 $ins[i]$ 时，该如何决策：
S 的最大值），说明 $ins[i]$ 完全不被 S 所覆盖，为满足题意，我们要在 $ins[i]$ 中选两个点，此时直观思路是选择 $ins[i]$ 最靠右的两个点（即 $ins[i][1] - 1$ 和 $ins[i][1]$）；S 存在一个重合点 b，由于次大值 a 和 最大值 b 不总是相差 $1$，我们不能写成 $ins[i][0] == b$），此时为了满足 $ins[i]$ 至少被 $2$ 个点覆盖，我们需要在 $ins[i]$ 中额外选择一个点，此时直观思路是选择 $ins[i]$ 最靠右的点（即$ins[i][1]$）；S 至少存在两个点 a 和 b，此时无须额外引入其余点来覆盖 $ins[i]$。上述情况是对「右端点从小到大」的必要性说明，而「左端点从大到小」目的是为了方便我们处理边界情况而引入的：若在右端点相同的情况下，如果「左端点从小到大」处理的话，会有重复的边缘点被加入 S。
有同学对重复边缘点加入
S不理解，假设S当前的次大值和最大值分别为j和k（其中 $k - j > 1$），如果后面有两个区间分别为 $[k - 1, d]$ 和 $[k + 1, d]$ 时，就会出现问题（其中d为满足条件的任意右端点）
更具体的：假设当前次大值和最大值分别为 $2$ 和 $4$，后续两个区间分别为 $[3, 8]$ 和 $[5, 8]$，你会发现先处理 $[3, 8]$ 的话，数值 $8$ 会被重复添加
上述决策存在直观判断，需要证明不存在比该做法取得的点集 S 更小的合法解：
若存在更小的合法集合方案 A（最优解），根据我们最前面对两个线段的重合分析知道，由于存在任意选点均能满足覆盖要求的情况，因此最优解 A 的具体方案可能并不唯一。
因此首先我们先在不影响 A 的集合大小的前提下，对具体方案 A 中的非关键点（即那些被选择，但既不是某个具体区间的边缘点，也不是边缘点的相邻点）进行调整（修改为区间边缘点或边缘点的相邻点）。
这样我们能够得到一个唯一的最优解具体方案，该方案既能取到最小点集大小，同时与贪心解 S 的选点有较大重合度。
此时如果贪心解并不是最优解的话，意味着贪心解中存在某些不必要的点（可去掉，同时不会影响覆盖要求）。
然后我们在回顾下，我们什么情况下会往 S 中进行加点，根据上述「不失一般性」的分析：
S 中添加两个点，若这个不必要的点是在这个分支中被添加的话，意味着当前 $ins[i]$ 可以不在此时被覆盖，而在后续其他区间 $ins[j]$ 被覆盖时被同步覆盖（其中 $j > i$），此时必然对应了我们重合分析中的后两种情况，可以将原本在 $ins[j]$ 中被选择的点，调整为 $ins[i]$ 的两个边缘点，结果不会变差（覆盖情况不变，点数不会变多）：
即此时原本在最优解 A 中不存在，在贪心解 S 中存在的「不必要点」会变成「必要点」。
S 中添加一个点，若这个不必要的点是在这个分支被添加的话，分析方式同理，且情况 $1$ 不会发生，如果 $ins[i]$ 和 $ins[j]$ 只有一个重合点的话，起始 $ins[i][1]$ 不会是不必要点：
综上，我们可以经过两步的“调整”，将贪心解变为最优解：第一步调整是在最优解的任意具体方案 A 中发生，通过将所有非边缘点调整为边缘点，来得到一个唯一的最优解具体方案；然后通过反证法证明，贪心解 S 中并不存在所谓的可去掉的「不必要点」，从而证明「贪心解大小必然不会大于最优解的大小」，即 $S > A$ 不成立，$S \leq A$ 恒成立，再结合 A 是最优解的前提（$A \leq S$），可得 $S = A$。
代码：
###Java
class Solution {
public int intersectionSizeTwo(int[][] ins) {
Arrays.sort(ins, (a, b)->{
return a[1] != b[1] ? a[1] - b[1] : b[0] - a[0];
});
int a = -1, b = -1, ans = 0;
for (int[] i : ins) {
if (i[0] > b) {
a = i[1] - 1; b = i[1];
ans += 2;
} else if (i[0] > a) {
a = b; b = i[1];
ans++;
}
}
return ans;
}
}
###TypeScript
function intersectionSizeTwo(ins: number[][]): number {
ins = ins.sort((a, b)=> {
return a[1] != b[1] ? a[1] - b[1] : b[0] - a[0]
});
let a = -1, b = -1, ans = 0
for (const i of ins) {
if (i[0] > b) {
a = i[1] - 1; b = i[1]
ans += 2
} else if (i[0] > a) {
a = b; b = i[1]
ans++
}
}
return ans
};
如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ ("▔□▔)/
也欢迎你 关注我 和 加入我们的「组队打卡」小群 ，提供写「证明」&「思路」的高质量题解。
所有题解已经加入 刷题指南，欢迎 star 哦 ~
我们对intervals进行排序，intervals[0]升序，inervals[1]降序，然后从后向前进行遍历。
为什么要一个升序一个降序呢？
假设我们有一个intervals = [[2,3]，[3,4]，[5,10]，[5,8]] (已排好序), 只要我们满足了和[5,8]的交集大于等于2，则对于[5,10]（左区间相同，右区间降序，保证在左区间相同的情况下让区间范围最小的在最右边）这个区间来说，必定是满足交集大于等于2的，因为小区间满足，大区间必然满足，反过来不一定，在左区间相同的情况下,我们取最小区间的两个元素就可以满足所有左区间相同的区间。因此我们贪心的取interval[n-1][0]和interval[n-1][0] + 1做为开始的两个集合元素，设初始两个元素为cur和next，则cur = intervals[n - 1][0],next = intervals[n - 1][0] + 1。
然后开始分类讨论上一个区间[xi,yi]的情况，根据排序有xi <= cur
yi >= next ,则是一个大区间，一定满足交集为2的情况yi < cur,那一定没有交集，我们还是贪心的取cur = xi,next = xi + 1
cur <= yi < next,有一个交集，我们贪心的取next = cur，cur = xi
class Solution {
public int intersectionSizeTwo(int[][] intervals) {
Arrays.sort(intervals, (o1, o2) -> o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]);
int n = intervals.length;
//初始的两个元素
int cur = intervals[n - 1][0];
int next = intervals[n - 1][0] + 1;
int ans = 2;
//从后向前遍历
for (int i = n - 2; i >= 0; i--) {
//开始分类讨论
if (intervals[i][1] >= next) {
continue;
} else if (intervals[i][1] < cur) {
cur = intervals[i][0];
next = intervals[i][0] + 1;
ans = ans + 2;
} else {
next = cur;
cur = intervals[i][0];
ans++;
}
}
return ans;
}
}
class Solution:
def intersectionSizeTwo(self, intervals: List[List[int]]) -> int:
if not intervals:
return 0
intervals.sort(key = lambda x : (x[0], -x[1]))
ans = 2
cur, next = intervals[-1][0], intervals[-1][0]+1
for xi, yi in reversed(intervals[:-1]):
if yi >= next:
continue
elif yi < cur:
cur = xi
next = xi + 1
ans += 2
elif cur <= yi < next:
next = cur
cur = xi
ans += 1
return ans
class Solution {
public:
int intersectionSizeTwo(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b){
if(a[0] == b[0]){
return a[1] > b[1];
}
return a[0] < b[0];
}); // 左边界升序，若相同，右边界降序
int res = 2, ls = intervals.back()[0], rs = ls + 1;
for(int i = intervals.size() - 2; i >= 0; i--){
if(intervals[i][1] >= rs){ // 有两个及以上的交点
continue;
}else if(intervals[i][1] < ls){ // 没有交点
ls = intervals[i][0];
rs = intervals[i][0] + 1;
res += 2;
}else{ // 一个交点
rs = ls;
ls = intervals[i][0];
res++;
}
}
return res;
}
};
感谢@fergus-peng小伙伴的py代码
感谢@handsomechar小伙伴的c++代码
给大家写了一个打印结果的代码，方便大家理解
代码如下
public int intersectionSizeTwo(int[][] intervals) {
Arrays.sort(intervals, (o1, o2) -> o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]);
System.out.println("排序后intervals：" + Arrays.deepToString(intervals));
int n = intervals.length;
int cur = intervals[n - 1][0];
int next = intervals[n - 1][0] + 1;
int ans = 2;
List<Integer> list = new ArrayList<>();
list.add(cur);
list.add(next);
for (int i = n - 2; i >= 0; i--) {
System.out.println("待比较区间：" + Arrays.toString(intervals[i]) + "\t当前集合S：" + list);
if (intervals[i][1] >= next) {
continue;
} else if (intervals[i][1] < cur) {
cur = intervals[i][0];
next = intervals[i][0] + 1;
ans = ans + 2;
list.add(0, next);
list.add(0, cur);
} else {
next = cur;
cur = intervals[i][0];
ans++;
list.add(0, cur);
}
}
return ans;
}
示例：
int[][] intervals = {{2, 10}, {3, 7}, {3, 15}, {4, 11}, {6, 12}, {6, 16}, {7, 8}, {7, 11}, {7, 15}, {11, 12}};
//结果
排序后intervals：[[2, 10], [3, 15], [3, 7], [4, 11], [6, 16], [6, 12], [7, 15], [7, 11], [7, 8], [11, 12]]
待比较区间：[7, 8]当前集合S：[11, 12]
待比较区间：[7, 11]当前集合S：[7, 8, 11, 12]
待比较区间：[7, 15]当前集合S：[7, 8, 11, 12]
待比较区间：[6, 12]当前集合S：[7, 8, 11, 12]
待比较区间：[6, 16]当前集合S：[7, 8, 11, 12]
待比较区间：[4, 11]当前集合S：[7, 8, 11, 12]
待比较区间：[3, 7]当前集合S：[7, 8, 11, 12]
待比较区间：[3, 15]当前集合S：[3, 7, 8, 11, 12]
待比较区间：[2, 10]当前集合S：[3, 7, 8, 11, 12]
写题解不易，如果对您有帮助，记得关注 + 点赞 + 收藏呦！！！
每天都会更新每日一题题解，大家加油！！
思路与算法
首先我们从稍简化的情况开始分析：如果题目条件为设置交集大小为 $1$，为了更好的分析我们将 $\textit{intervals}$ 按照 $[s,e]$ 序对进行升序排序，其中 $\textit{intervals}$ 为题目给出的区间集合，$s,e$ 为区间的左右边界。设排序后的 $\textit{intervals} = {[s_1,e_1,],\dots,[s_n,e_n]}$，其中 $n$ 为区间集合的大小，并满足 $\forall i,j \in [1,n],i < j$ 有 $s_i \leq s_j$ 成立。然后对于最后一个区间 $[s_n,e_n]$ 来说一定是要提供一个最后交集集合中的元素，那么我们思考我们选择该区间中哪个元素是最优的——最优的元素应该尽可能的把之前的区间尽可能的覆盖。那么我们选择该区间的开头元素 $s_n$ 一定是最优的，因为对于前面的某一个区间 $[s_i,s_j]$：
即对于最后一个区间 $[s_n，e_n]$ 来说选择区间的开头元素 $s_n$ 一定是最优的。那么贪心的思路就出来了：排序后从后往前进行遍历，每次选取与当前交集集合相交为空的区间的最左边的元素即可，然后往前判断前面是否有区间能因此产生交集，产生交集的直接跳过即可。此时算法的时间复杂度为：$O(n \log n)$ 主要为排序的时间复杂度。对于这种情况具体也可以见本站题目 452. 用最少数量的箭引爆气球。
那么我们用同样的思路来扩展到需要交集为 $m~,~m > 1$ 的情况：此时同样首先对 $\textit{intervals}$ 按照 $[s,e]$ 序对进行升序排序，然后我们需要额外记录每一个区间与最后交集集合中相交的元素（只记录到 $m$ 个为止）。同样我们从最后一个区间往前进行处理，如果该区间与交集集合相交元素个数小于 $m$ 个时，我们从该区间左边界开始往后添加不在交集集合中的元素，并往前进行更新需要更新的区间，重复该过程直至该区间与交集元素集合有 $m$ 个元素相交。到此就可以解决问题了，不过我们也可以来修改排序的规则——我们将区间 $[s,e]$ 序对按照 $s$ 升序，当 $s$ 相同时按照 $e$ 降序来进行排序，这样可以实现在处理与交集集合相交元素个数小于 $m$ 个的区间 $[s_i,e_i]$ 时，保证不足的元素都是在区间的开始部分，即我们可以直接从区间开始部分进行往交集集合中添加元素。
而对于本题来说，我们只需要取 $m = 2$ 的情况即可。
代码
###Python
class Solution:
def intersectionSizeTwo(self, intervals: List[List[int]]) -> int:
intervals.sort(key=lambda x: (x[0], -x[1]))
ans, n, m = 0, len(intervals), 2
vals = [[] for _ in range(n)]
for i in range(n - 1, -1, -1):
j = intervals[i][0]
for k in range(len(vals[i]), m):
ans += 1
for p in range(i - 1, -1, -1):
if intervals[p][1] < j:
break
vals[p].append(j)
j += 1
return ans
###C++
class Solution {
public:
void help(vector<vector<int>>& intervals, vector<vector<int>>& temp, int pos, int num) {
for (int i = pos; i >= 0; i--) {
if (intervals[i][1] < num) {
break;
}
temp[i].push_back(num);
}
}
int intersectionSizeTwo(vector<vector<int>>& intervals) {
int n = intervals.size();
int res = 0;
int m = 2;
sort(intervals.begin(), intervals.end(), [&](vector<int>& a, vector<int>& b) {
if (a[0] == b[0]) {
return a[1] > b[1];
}
return a[0] < b[0];
});
vector<vector<int>> temp(n);
for (int i = n - 1; i >= 0; i--) {
for (int j = intervals[i][0], k = temp[i].size(); k < m; j++, k++) {
res++;
help(intervals, temp, i - 1, j);
}
}
return res;
}
};
###Java
class Solution {
public int intersectionSizeTwo(int[][] intervals) {
int n = intervals.length;
int res = 0;
int m = 2;
Arrays.sort(intervals, (a, b) -> {
if (a[0] == b[0]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
List<Integer>[] temp = new List[n];
for (int i = 0; i < n; i++) {
temp[i] = new ArrayList<Integer>();
}
for (int i = n - 1; i >= 0; i--) {
for (int j = intervals[i][0], k = temp[i].size(); k < m; j++, k++) {
res++;
help(intervals, temp, i - 1, j);
}
}
return res;
}
public void help(int[][] intervals, List<Integer>[] temp, int pos, int num) {
for (int i = pos; i >= 0; i--) {
if (intervals[i][1] < num) {
break;
}
temp[i].add(num);
}
}
}
###C#
public class Solution {
public int IntersectionSizeTwo(int[][] intervals) {
int n = intervals.Length;
int res = 0;
int m = 2;
Array.Sort(intervals, (a, b) => {
if (a[0] == b[0]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
IList<int>[] temp = new IList<int>[n];
for (int i = 0; i < n; i++) {
temp[i] = new List<int>();
}
for (int i = n - 1; i >= 0; i--) {
for (int j = intervals[i][0], k = temp[i].Count; k < m; j++, k++) {
res++;
Help(intervals, temp, i - 1, j);
}
}
return res;
}
public void Help(int[][] intervals, IList<int>[] temp, int pos, int num) {
for (int i = pos; i >= 0; i--) {
if (intervals[i][1] < num) {
break;
}
temp[i].Add(num);
}
}
}
###C
static void help(int** intervals, int** temp, int *colSize, int pos, int num) {
for (int i = pos; i >= 0; i --) {
if (intervals[i][1] < num) {
break;
}
temp[i][colSize[i]++] = num;
}
}
static inline int cmp(const void* pa, const void* pb) {
if ((*(int **)pa)[0] == (*(int **)pb)[0]) {
return (*(int **)pb)[1] - (*(int **)pa)[1];
}
return (*(int **)pa)[0] - (*(int **)pb)[0];
}
int intersectionSizeTwo(int** intervals, int intervalsSize, int* intervalsColSize){
int res = 0;
int m = 2;
qsort(intervals, intervalsSize, sizeof(int *), cmp);
int **temp = (int **)malloc(sizeof(int *) * intervalsSize);
for (int i = 0; i < intervalsSize; i++) {
temp[i] = (int *)malloc(sizeof(int) * 2);
}
int *colSize = (int *)malloc(sizeof(int) * intervalsSize);
memset(colSize, 0, sizeof(int) * intervalsSize);
for (int i = intervalsSize - 1; i >= 0; i --) {
for (int j = intervals[i][0], k = colSize[i]; k < m; j++, k++) {
res++;
help(intervals, temp, colSize, i - 1, j);
}
}
for (int i = 0; i < intervalsSize; i++) {
free(temp[i]);
}
free(colSize);
return res;
}
###go
func intersectionSizeTwo(intervals [][]int) (ans int) {
sort.Slice(intervals, func(i, j int) bool {
a, b := intervals[i], intervals[j]
return a[0] < b[0] || a[0] == b[0] && a[1] > b[1]
})
n, m := len(intervals), 2
vals := make([][]int, n)
for i := n - 1; i >= 0; i-- {
for j, k := intervals[i][0], len(vals[i]); k < m; k++ {
ans++
for p := i - 1; p >= 0 && intervals[p][1] >= j; p-- {
vals[p] = append(vals[p], j)
}
j++
}
}
return
}
###JavaScript
var intersectionSizeTwo = function(intervals) {
const n = intervals.length;
let res = 0;
let m = 2;
intervals.sort((a, b) => {
if (a[0] === b[0]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
const temp = new Array(n).fill(0);
for (let i = 0; i < n; i++) {
temp[i] = [];
}
const help = (intervals, temp, pos, num) => {
for (let i = pos; i >= 0; i--) {
if (intervals[i][1] < num) {
break;
}
temp[i].push(num);
}
}
for (let i = n - 1; i >= 0; i--) {
for (let j = intervals[i][0], k = temp[i].length; k < m; j++, k++) {
res++;
help(intervals, temp, i - 1, j);
}
}
return res;
};
复杂度分析
时间复杂度：$O(n \log n + nm)$，其中 $n$ 为给定区间集合 $\textit{intervals}$ 的大小，$m$ 为设置交集大小，本题为 $2$。
空间复杂度：$O(nm)$，其中 $n$ 为给定区间集合 $\textit{intervals}$ 的大小，$m$ 为设置交集的大小，本题为 $2$。主要开销为存储每一个区间与交集集合的相交的元素的开销。
思路与算法
如果我们不对数组 $\textit{nums}$ 进行任何操作，那么每次更新 $\textit{original}$ 后，都需要 $O(n)$ 的时间完整遍历一遍。最终时间复杂度为 $O(n^2)$。
我们可以对这一过程进行优化。具体而言，每次在数组中找到 $\textit{original}$ 后，$\textit{original}$ 的数值都会比更新前更大，因此我们可以先将数组 $\textit{nums}$ 升序排序，这样每次更新后的 $\textit{original}$ 数值在数组中的位置（如有）只可能位于更新前的后面，我们只需要一边从左至右遍历排序后的 $\textit{nums}$ 数组一边尝试更新 $\textit{original}$ 即可。
代码
###C++
class Solution {
public:
int findFinalValue(vector<int>& nums, int original) {
sort(nums.begin(), nums.end());
for (int num: nums) {
if (original == num) {
original *= 2;
}
}
return original;
}
};
###Python
class Solution:
def findFinalValue(self, nums: List[int], original: int) -> int:
nums.sort()
for num in nums:
if num == original:
original *= 2
return original
###Java
class Solution {
public int findFinalValue(int[] nums, int original) {
Arrays.sort(nums);
for (int num : nums) {
if (original == num) {
original *= 2;
}
}
return original;
}
}
###C#
public class Solution {
public int FindFinalValue(int[] nums, int original) {
Array.Sort(nums);
foreach (int num in nums) {
if (original == num) {
original *= 2;
}
}
return original;
}
}
###Go
func findFinalValue(nums []int, original int) int {
sort.Ints(nums)
for _, num := range nums {
if original == num {
original *= 2
}
}
return original
}
###C
int cmp(const void* a, const void* b) {
return (*(int*)a - *(int*)b);
}
int findFinalValue(int* nums, int numsSize, int original) {
qsort(nums, numsSize, sizeof(int), cmp);
for (int i = 0; i < numsSize; i++) {
if (original == nums[i]) {
original *= 2;
}
}
return original;
}
###JavaScript
var findFinalValue = function(nums, original) {
nums.sort((a, b) => a - b);
for (const num of nums) {
if (original === num) {
original *= 2;
}
}
return original;
};
###TypeScript
function findFinalValue(nums: number[], original: number): number {
nums.sort((a, b) => a - b);
for (const num of nums) {
if (original === num) {
original *= 2;
}
}
return original;
}
###Rust
impl Solution {
pub fn find_final_value(nums: Vec<i32>, original: i32) -> i32 {
let mut nums = nums;
nums.sort();
let mut original = original;
for &num in nums.iter() {
if original == num {
original *= 2;
}
}
original
}
}
复杂度分析
时间复杂度：$O(n \log n)$，其中 $n$ 为 $\textit{nums}$ 的长度。排序的时间复杂度为 $O(n \log n)$，遍历更新 $\textit{original}$ 的时间复杂度最多为 $O(n)$。
空间复杂度：$O(\log n)$，即为排序的栈空间开销。
思路与算法
我们还可以采用更加直接地利用空间换取时间的方法：利用哈希集合存储数组 $\textit{nums}$ 中的元素，然后我们只需要每次判断 $\textit{original}$ 是否位于该哈希集合中即可。具体地：
如果 $\textit{original}$ 位于哈希集合中，我们将 $\textit{original}$ 乘以 $2$，然后再次判断；
如果 $\textit{original}$ 不位于哈希集合中，那么循环结束，我们返回当前的 $\textit{original}$ 作为答案。
代码
###C++
class Solution {
public:
int findFinalValue(vector<int>& nums, int original) {
unordered_set<int> s(nums.begin(), nums.end());
while (s.count(original)) {
original *= 2;
}
return original;
}
};
###Python
class Solution:
def findFinalValue(self, nums: List[int], original: int) -> int:
s = set(nums)
while original in s:
original *= 2
return original
###Java
class Solution {
public int findFinalValue(int[] nums, int original) {
Set<Integer> set = new HashSet<>();
for (int num : nums) {
set.add(num);
}
while (set.contains(original)) {
original *= 2;
}
return original;
}
}
###C#
public class Solution {
public int FindFinalValue(int[] nums, int original) {
HashSet<int> set = new HashSet<int>(nums);
while (set.Contains(original)) {
original *= 2;
}
return original;
}
}
###Go
func findFinalValue(nums []int, original int) int {
set := make(map[int]bool)
for _, num := range nums {
set[num] = true
}
for set[original] {
original *= 2
}
return original
}
###C
typedef struct {
int key;
UT_hash_handle hh;
} HashItem;
HashItem *hashFindItem(HashItem **obj, int key) {
HashItem *pEntry = NULL;
HASH_FIND_INT(*obj, &key, pEntry);
return pEntry;
}
bool hashAddItem(HashItem **obj, int key) {
if (hashFindItem(obj, key)) {
return false;
}
HashItem *pEntry = (HashItem *)malloc(sizeof(HashItem));
pEntry->key = key;
HASH_ADD_INT(*obj, key, pEntry);
return true;
}
void hashFree(HashItem **obj) {
HashItem *curr = NULL, *tmp = NULL;
HASH_ITER(hh, *obj, curr, tmp) {
HASH_DEL(*obj, curr);
free(curr);
}
}
int findFinalValue(int* nums, int numsSize, int original) {
HashItem *set = NULL;
for (int i = 0; i < numsSize; i++) {
hashAddItem(&set, nums[i]);
}
while (hashFindItem(&set, original)) {
original *= 2;
}
hashFree(&set);
return original;
}
###JavaScript
var findFinalValue = function(nums, original) {
const set = new Set(nums);
while (set.has(original)) {
original *= 2;
}
return original;
};
###TypeScript
function findFinalValue(nums: number[], original: number): number {
const set = new Set(nums);
while (set.has(original)) {
original *= 2;
}
return original;
}
###Rust
use std::collections::HashSet;
impl Solution {
pub fn find_final_value(nums: Vec<i32>, original: i32) -> i32 {
let set: HashSet<_> = nums.into_iter().collect();
let mut original = original;
while set.contains(&original) {
original *= 2;
}
original
}
}
复杂度分析
时间复杂度：$O(n)$，其中 $n$ 为 $\textit{nums}$ 的长度。遍历数组维护元素哈希集合的时间复杂度为 $O(n)$，遍历更新 $\textit{original}$ 的时间复杂度最多为 $O(n)$。
空间复杂度：$O(n)$，即为元素哈希集合的空间开销。
我们用一个哈希表 $\textit{s}$ 记录数组 $\textit{nums}$ 中的所有数字。
接下来，我们从 $\textit{original}$ 开始，如果 $\textit{original}$ 在 $\textit{s}$ 中，我们将 $\textit{original}$ 乘以 $2$，直到 $\textit{original}$ 不在 $\textit{s}$ 中，返回 $\textit{original}$。
###python
class Solution:
def findFinalValue(self, nums: List[int], original: int) -> int:
s = set(nums)
while original in s:
original <<= 1
return original
###java
class Solution {
public int findFinalValue(int[] nums, int original) {
Set<Integer> s = new HashSet<>();
for (int num : nums) {
s.add(num);
}
while (s.contains(original)) {
original <<= 1;
}
return original;
}
}
###cpp
class Solution {
public:
int findFinalValue(vector<int>& nums, int original) {
unordered_set<int> s(nums.begin(), nums.end());
while (s.contains(original)) {
original <<= 1;
}
return original;
}
};
###go
func findFinalValue(nums []int, original int) int {
s := map[int]bool{}
for _, x := range nums {
s[x] = true
}
for s[original] {
original <<= 1
}
return original
}
###ts
function findFinalValue(nums: number[], original: number): number {
const s: Set<number> = new Set([...nums]);
while (s.has(original)) {
original <<= 1;
}
return original;
}
###rust
impl Solution {
pub fn find_final_value(nums: Vec<i32>, original: i32) -> i32 {
use std::collections::HashSet;
let s: HashSet<i32> = nums.into_iter().collect();
let mut original = original;
while s.contains(&original) {
original <<= 1;
}
original
}
}
时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为数组 $\textit{nums}$ 的长度。
有任何问题，欢迎评论区交流，欢迎评论区提供其它解题思路（代码），也可以点个赞支持一下作者哈 😄~
