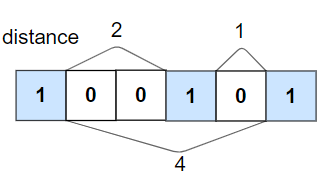
通用解法:栈+二分查找(Python/Java/C++/Go)
把 $2$ 改成 $k$ 怎么做?
更一般地,每个区间要包含的数字个数各有不同,怎么做?
这题是 2589. 完成所有任务的最少时间,我的题解。
class Solution:
def intersectionSizeTwo(self, intervals: List[List[int]]) -> int:
intervals.sort(key=lambda interval: interval[1])
# 栈中保存闭区间左右端点,栈底到栈顶的区间长度的和
st = [(-2, -2, 0)] # 哨兵,保证不和任何区间相交
for start, end in intervals:
_, r, s = st[bisect_left(st, (start,)) - 1]
d = 2 - (st[-1][2] - s) # 去掉运行中的时间点
if start <= r: # start 在区间 st[i] 内
d -= r - start + 1 # 去掉运行中的时间点
if d <= 0:
continue
while end - st[-1][1] <= d: # 剩余的 d 填充区间后缀
l, r, _ = st.pop()
d += r - l + 1 # 合并区间
st.append((end - d + 1, end, st[-1][2] + d))
return st[-1][2]
class Solution {
public int intersectionSizeTwo(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> a[1] - b[1]);
// 栈中保存闭区间左右端点,栈底到栈顶的区间长度的和
List<int[]> st = new ArrayList<>();
st.add(new int[]{-2, -2, 0}); // 哨兵,保证不和任何区间相交
for (int[] t : intervals) {
int start = t[0], end = t[1];
int[] e = st.get(lowerBound(st, start) - 1);
int d = 2 - (st.get(st.size() - 1)[2] - e[2]); // 去掉运行中的时间点
if (start <= e[1]) { // start 在区间 st[i] 内
d -= e[1] - start + 1; // 去掉运行中的时间点
}
if (d <= 0) {
continue;
}
while (end - st.get(st.size() - 1)[1] <= d) { // 剩余的 d 填充区间后缀
e = st.remove(st.size() - 1);
d += e[1] - e[0] + 1; // 合并区间
}
st.add(new int[]{end - d + 1, end, st.get(st.size() - 1)[2] + d});
}
return st.get(st.size() - 1)[2];
}
// 开区间二分
// 见 https://www.bilibili.com/video/BV1AP41137w7/
private int lowerBound(List<int[]> st, int target) {
int left = -1, right = st.size(); // 开区间 (left, right)
while (left + 1 < right) { // 区间不为空
// 循环不变量:
// st[left] < target
// st[right] >= target
int mid = (left + right) >>> 1;
if (st.get(mid)[0] < target) {
left = mid; // 范围缩小到 (mid, right)
} else {
right = mid; // 范围缩小到 (left, mid)
}
}
return right;
}
}
class Solution {
public:
int intersectionSizeTwo(vector<vector<int>>& intervals) {
ranges::sort(intervals, {}, [](auto& a) { return a[1]; });
// 栈中保存闭区间左右端点,栈底到栈顶的区间长度的和
vector<array<int, 3>> st = {{-2, -2, 0}}; // 哨兵,保证不和任何区间相交
for (auto& t : intervals) {
int start = t[0], end = t[1];
auto [_, r, s] = *--ranges::lower_bound(st, start, {}, [](auto& x) { return x[0]; });
int d = 2 - (st.back()[2] - s); // 去掉运行中的时间点
if (start <= r) { // start 在区间 st[i] 内
d -= r - start + 1; // 去掉运行中的时间点
}
if (d <= 0) {
continue;
}
while (end - st.back()[1] <= d) { // 剩余的 d 填充区间后缀
auto [l, r, _] = st.back();
st.pop_back();
d += r - l + 1; // 合并区间
}
st.push_back({end - d + 1, end, st.back()[2] + d});
}
return st.back()[2];
}
};
func intersectionSizeTwo(intervals [][]int) int {
slices.SortFunc(intervals, func(a, b []int) int { return a[1] - b[1] })
// 栈中保存闭区间左右端点,栈底到栈顶的区间长度的和
type tuple struct{ l, r, s int }
st := []tuple{{-2, -2, 0}} // 哨兵,保证不和任何区间相交
for _, p := range intervals {
start, end := p[0], p[1]
i := sort.Search(len(st), func(i int) bool { return st[i].l >= start }) - 1
d := 2 - (st[len(st)-1].s - st[i].s) // 去掉运行中的时间点
if start <= st[i].r { // start 在区间 st[i] 内
d -= st[i].r - start + 1 // 去掉运行中的时间点
}
if d <= 0 {
continue
}
for end-st[len(st)-1].r <= d { // 剩余的 d 填充区间后缀
top := st[len(st)-1]
st = st[:len(st)-1]
d += top.r - top.l + 1 // 合并区间
}
st = append(st, tuple{end - d + 1, end, st[len(st)-1].s + d})
}
return st[len(st)-1].s
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n\log n)$,其中 $n$ 是 $\textit{intervals}$ 的长度。
- 空间复杂度:$\mathcal{O}(n)$。
相似题目
见下面贪心题单的「§2.3 区间选点」。
分类题单
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 二分算法(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流)
- 动态规划(入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)
欢迎关注 B站@灵茶山艾府