前言
设 $\textit{strs}[i]$ 中 $0$ 的个数为 $\textit{cnt}_0[i]$,$1$ 的个数为 $\textit{cnt}_1[i]$,那么本题相当于:
- 有一个容量为 $(m,n)$ 的背包,至多可以装入 $m$ 个 $0$ 和 $n$ 个 $1$。现在有 $n$ 个物品,每个物品的体积为 $(\textit{cnt}_0[i],\textit{cnt}_1[i])$,表示该物品有 $\textit{cnt}_0[i]$ 个 $0$ 和 $\textit{cnt}_1[i]$ 个 $1$。问:最多可以选多少个物品?
这相当于背包有两种体积(二维),所以在定义状态的时候,相比只有一种体积的 0-1 背包,要多加一个参数。
如果你不了解 0-1 背包,请看【基础算法精讲 18】。
一、记忆化搜索
在一维 0-1 背包的基础上,多加一个参数,即定义 $\textit{dfs}(i,j,k)$ 表示在 $[0,i]$ 中选字符串,在 $0$ 的个数至多为 $j$,$1$ 的个数至多为 $k$ 的约束下,至多可以选多少个字符串。
考虑 $\textit{strs}[i]$ 选或不选:
- 不选:问题变成在 $[0,i-1]$ 中选字符串,在 $0$ 的个数至多为 $j$,$1$ 的个数至多为 $k$ 的约束下,至多可以选多少个字符串,即 $\textit{dfs}(i,j,k) = \textit{dfs}(i-1,j,k)$。
- 选:如果 $j\ge \textit{cnt}_0[i]$ 并且 $k\ge \textit{cnt}_1[i]$ 则可以选。问题变成在 $[0,i-1]$ 中选字符串,在 $0$ 的个数至多为 $j-\textit{cnt}_0[i]$,$1$ 的个数至多为 $k-\textit{cnt}_1[i]$ 的约束下,至多可以选多少个字符串,即 $\textit{dfs}(i,j,k) = \textit{dfs}(i-1,j-\textit{cnt}_0[i],k-\textit{cnt}_1[i]) + 1$。
两种情况取最大值,得
$$
\textit{dfs}(i,j,k) = \max(\textit{dfs}(i-1,j,k), \textit{dfs}(i-1,j-\textit{cnt}_0[i],k-\textit{cnt}_1[i]) + 1)
$$
如果
递归边界:$\textit{dfs}(-1,j,k)=0$。此时没有物品可以选。
递归入口:$\textit{dfs}(k-1,m,n)$,这是原问题,也是答案。其中 $k$ 为 $\textit{strs}$ 的长度。
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
cnt0 = [s.count('0') for s in strs]
@cache # 缓存装饰器,避免重复计算 dfs 的结果(记忆化)
def dfs(i: int, j: int, k: int) -> int:
if i < 0:
return 0
res = dfs(i - 1, j, k) # 不选 strs[i]
cnt1 = len(strs[i]) - cnt0[i]
if j >= cnt0[i] and k >= cnt1:
res = max(res, dfs(i - 1, j - cnt0[i], k - cnt1) + 1) # 选 strs[i]
return res
return dfs(len(strs) - 1, m, n)
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int k = strs.length;
int[] cnt0 = new int[k];
for (int i = 0; i < k; i++) {
cnt0[i] = (int) strs[i].chars().filter(ch -> ch == '0').count();
}
int[][][] memo = new int[strs.length][m + 1][n + 1];
for (int[][] mat : memo) {
for (int[] arr : mat) {
Arrays.fill(arr, -1); // -1 表示没有计算过
}
}
return dfs(k - 1, m, n, strs, cnt0, memo);
}
private int dfs(int i, int j, int k, String[] strs, int[] cnt0, int[][][] memo) {
if (i < 0) {
return 0;
}
if (memo[i][j][k] != -1) { // 之前计算过
return memo[i][j][k];
}
// 不选 strs[i]
int res = dfs(i - 1, j, k, strs, cnt0, memo);
int cnt1 = strs[i].length() - cnt0[i];
if (j >= cnt0[i] && k >= cnt1) {
// 选 strs[i]
res = Math.max(res, dfs(i - 1, j - cnt0[i], k - cnt1, strs, cnt0, memo) + 1);
}
return memo[i][j][k] = res; // 记忆化
}
}
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<int> cnt0(strs.size());
for (int i = 0; i < strs.size(); i++) {
cnt0[i] = ranges::count(strs[i], '0');
}
vector memo(strs.size(), vector(m + 1, vector<int>(n + 1, -1))); // -1 表示没有计算过
auto dfs = [&](this auto&& dfs, int i, int j, int k) -> int {
if (i < 0) {
return 0;
}
int& res = memo[i][j][k]; // 注意这里是引用
if (res != -1) { // 之前计算过
return res;
}
res = dfs(i - 1, j, k); // 不选 strs[i]
int cnt1 = strs[i].size() - cnt0[i];
if (j >= cnt0[i] && k >= cnt1) {
res = max(res, dfs(i - 1, j - cnt0[i], k - cnt1) + 1); // 选 strs[i]
}
return res;
};
return dfs(strs.size() - 1, m, n);
}
};
func findMaxForm(strs []string, m, n int) int {
k := len(strs)
cnt0 := make([]int, k)
for i, s := range strs {
cnt0[i] = strings.Count(s, "0")
}
memo := make([][][]int, k)
for i := range memo {
memo[i] = make([][]int, m+1)
for j := range memo[i] {
memo[i][j] = make([]int, n+1)
for k := range memo[i][j] {
memo[i][j][k] = -1 // -1 表示没有计算过
}
}
}
var dfs func(int, int, int) int
dfs = func(i, j, k int) int {
if i < 0 {
return 0
}
p := &memo[i][j][k]
if *p != -1 { // 之前计算过
return *p
}
res := dfs(i-1, j, k) // 不选 strs[i]
cnt1 := len(strs[i]) - cnt0[i]
if j >= cnt0[i] && k >= cnt1 {
res = max(res, dfs(i-1, j-cnt0[i], k-cnt1)+1) // 选 strs[i]
}
*p = res // 记忆化
return res
}
return dfs(k-1, m, n)
}
复杂度分析
- 时间复杂度:$\mathcal{O}(kmn+L)$,其中 $k$ 为 $\textit{strs}$ 的长度,$L$ 为 $\textit{strs}$ 中所有字符串的长度之和。由于每个状态只会计算一次,动态规划的时间复杂度 $=$ 状态个数 $\times$ 单个状态的计算时间。本题状态个数等于 $\mathcal{O}(kmn)$,单个状态的计算时间为 $\mathcal{O}(1)$,所以总的时间复杂度为 $\mathcal{O}(kmn)$。
- 空间复杂度:$\mathcal{O}(kmn)$。保存多少状态,就需要多少空间。
二、1:1 翻译成递推
我们可以去掉递归中的「递」,只保留「归」的部分,即自底向上计算。
具体来说,$f[i+1][j][k]$ 的定义和 $\textit{dfs}(i,j,k)$ 的定义是一样的,都表示在 $[0,i]$ 中选字符串,在 $0$ 的个数至多为 $j$,$1$ 的个数至多为 $k$ 的约束下,至多可以选多少个字符串。这里 $+1$ 是为了把 $\textit{dfs}(-1,j,k)$ 这个状态也翻译过来,这样我们可以把 $f[0][j][k]$ 作为初始值。
相应的递推式(状态转移方程)也和 $\textit{dfs}$ 一样:
$$
f[i+1][j][k] = \max(f[i][j][k], f[i][j-\textit{cnt}_0[i]][k-\textit{cnt}_1[i]] + 1)
$$
初始值 $f[0][j][k]=0$,翻译自递归边界 $\textit{dfs}(-1,j,k)=0$。
答案为 $f[k][m][n]$,翻译自递归入口 $\textit{dfs}(k-1,m,n)$。其中 $k$ 为 $\textit{strs}$ 的长度。
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
f = [[[0] * (n + 1) for _ in range(m + 1)] for _ in range(len(strs) + 1)]
for i, s in enumerate(strs):
cnt0 = s.count('0')
cnt1 = len(s) - cnt0
for j in range(m + 1):
for k in range(n + 1):
if j >= cnt0 and k >= cnt1:
f[i + 1][j][k] = max(f[i][j][k], f[i][j - cnt0][k - cnt1] + 1)
else:
f[i + 1][j][k] = f[i][j][k]
return f[-1][m][n]
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][][] f = new int[strs.length + 1][m + 1][n + 1];
for (int i = 0; i < strs.length; i++) {
int cnt0 = (int) strs[i].chars().filter(ch -> ch == '0').count();
int cnt1 = strs[i].length() - cnt0;
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
if (j >= cnt0 && k >= cnt1) {
f[i + 1][j][k] = Math.max(f[i][j][k], f[i][j - cnt0][k - cnt1] + 1);
} else {
f[i + 1][j][k] = f[i][j][k];
}
}
}
}
return f[strs.length][m][n];
}
}
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector f(strs.size() + 1, vector(m + 1, vector<int>(n + 1)));
for (int i = 0; i < strs.size(); i++) {
int cnt0 = ranges::count(strs[i], '0');
int cnt1 = strs[i].size() - cnt0;
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
if (j >= cnt0 && k >= cnt1) {
f[i + 1][j][k] = max(f[i][j][k], f[i][j - cnt0][k - cnt1] + 1);
} else {
f[i + 1][j][k] = f[i][j][k];
}
}
}
}
return f.back()[m][n];
}
};
func findMaxForm(strs []string, m, n int) int {
k := len(strs)
f := make([][][]int, k+1)
for i := range f {
f[i] = make([][]int, m+1)
for j := range f[i] {
f[i][j] = make([]int, n+1)
}
}
for i, s := range strs {
cnt0 := strings.Count(s, "0")
cnt1 := len(s) - cnt0
for j := range m + 1 {
for k := range n + 1 {
if j >= cnt0 && k >= cnt1 {
f[i+1][j][k] = max(f[i][j][k], f[i][j-cnt0][k-cnt1]+1)
} else {
f[i+1][j][k] = f[i][j][k]
}
}
}
}
return f[k][m][n]
}
复杂度分析
- 时间复杂度:$\mathcal{O}(kmn+L)$,其中 $k$ 为 $\textit{strs}$ 的长度,$L$ 为 $\textit{strs}$ 中所有字符串的长度之和。
- 空间复杂度:$\mathcal{O}(kmn)$。
三、空间优化
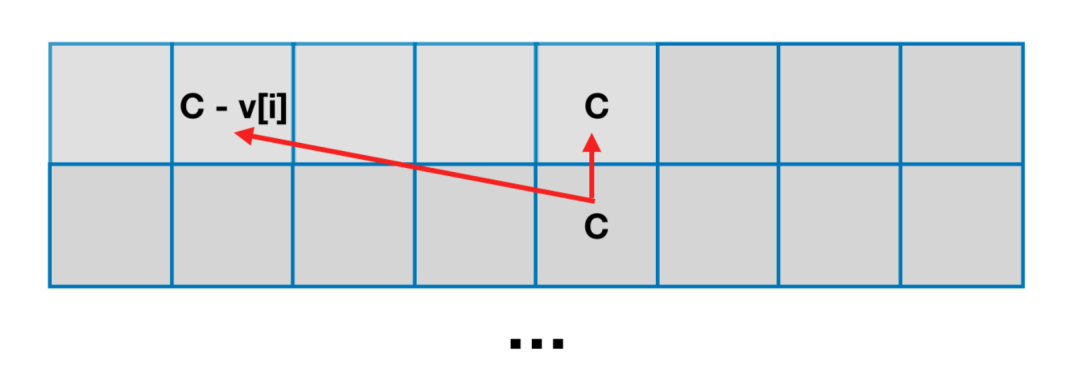
观察上面的状态转移方程,在计算 $f[i+1]$ 时,只会用到 $f[i]$,不会用到比 $i$ 更早的状态。
那么去掉第一个维度,把 $f[i+1]$ 和 $f[i]$ 保存到同一个二维数组中。
状态转移方程改为
$$
f[j][k] = \max(f[j][k], f[j-\textit{cnt}_0[i]][k-\textit{cnt}_1[i]] + 1)
$$
初始值 $f[j][k]=0$。
答案为 $f[m][n]$。
下面代码为什么要倒序循环,请看【基础算法精讲 18】。
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
f = [[0] * (n + 1) for _ in range(m + 1)]
for s in strs:
cnt0 = s.count('0')
cnt1 = len(s) - cnt0
for j in range(m, cnt0 - 1, -1):
for k in range(n, cnt1 - 1, -1):
f[j][k] = max(f[j][k], f[j - cnt0][k - cnt1] + 1)
return f[m][n]
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] f = new int[m + 1][n + 1];
for (String s : strs) {
int cnt0 = (int) s.chars().filter(ch -> ch == '0').count();
int cnt1 = s.length() - cnt0;
for (int j = m; j >= cnt0; j--) {
for (int k = n; k >= cnt1; k--) {
f[j][k] = Math.max(f[j][k], f[j - cnt0][k - cnt1] + 1);
}
}
}
return f[m][n];
}
}
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector f(m + 1, vector<int>(n + 1));
for (string& s : strs) {
int cnt0 = ranges::count(s, '0');
int cnt1 = s.size() - cnt0;
for (int j = m; j >= cnt0; j--) {
for (int k = n; k >= cnt1; k--) {
f[j][k] = max(f[j][k], f[j - cnt0][k - cnt1] + 1);
}
}
}
return f[m][n];
}
};
func findMaxForm(strs []string, m, n int) int {
f := make([][]int, m+1)
for i := range f {
f[i] = make([]int, n+1)
}
for _, s := range strs {
cnt0 := strings.Count(s, "0")
cnt1 := len(s) - cnt0
for j := m; j >= cnt0; j-- {
for k := n; k >= cnt1; k-- {
f[j][k] = max(f[j][k], f[j-cnt0][k-cnt1]+1)
}
}
}
return f[m][n]
}
进一步优化
比如 $n=m=90$,前 $3$ 个字符串总共有 $5$ 个 $0$ 和 $6$ 个 $1$,那么无论我们怎么选,也选不出几十个 $0$ 和 $1$,所以上面的代码中,其实有大量的循环是多余的。
为此,额外用两个变量 $\textit{sum}_0$ 和 $\textit{sum}_1$ 分别维护前 $i$ 个字符串中的 $0$ 的个数和 $1$ 的个数(但不能超过 $m$ 和 $n$)。循环的时候 $j$ 从 $\textit{sum}_0$ 开始,$k$ 从 $\textit{sum}_1$ 开始。
注意这个优化会导致只有一部分 $f[j][k]$ 被更新到,最大值并没有传递给 $f[m][n]$,可能留在二维数组中间的某个位置上。所以最后要遍历 $f$,取其中最大值作为答案。
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
f = [[0] * (n + 1) for _ in range(m + 1)]
sum0 = sum1 = 0
for s in strs:
cnt0 = s.count('0')
cnt1 = len(s) - cnt0
sum0 = min(sum0 + cnt0, m)
sum1 = min(sum1 + cnt1, n)
for j in range(sum0, cnt0 - 1, -1):
for k in range(sum1, cnt1 - 1, -1):
v = f[j - cnt0][k - cnt1] + 1
if v > f[j][k]: # 手写 max,效率更高
f[j][k] = v
return max(map(max, f))
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] f = new int[m + 1][n + 1];
int sum0 = 0;
int sum1 = 0;
for (String s : strs) {
int cnt0 = (int) s.chars().filter(ch -> ch == '0').count();
int cnt1 = s.length() - cnt0;
sum0 = Math.min(sum0 + cnt0, m);
sum1 = Math.min(sum1 + cnt1, n);
for (int j = sum0; j >= cnt0; j--) {
for (int k = sum1; k >= cnt1; k--) {
f[j][k] = Math.max(f[j][k], f[j - cnt0][k - cnt1] + 1);
}
}
}
int ans = 0;
for (int[] row : f) {
for (int v : row) {
ans = Math.max(ans, v);
}
}
return ans;
}
}
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector f(m + 1, vector<int>(n + 1));
int sum0 = 0, sum1 = 0;
for (string& s : strs) {
int cnt0 = ranges::count(s, '0');
int cnt1 = s.size() - cnt0;
sum0 = min(sum0 + cnt0, m);
sum1 = min(sum1 + cnt1, n);
for (int j = sum0; j >= cnt0; j--) {
for (int k = sum1; k >= cnt1; k--) {
f[j][k] = max(f[j][k], f[j - cnt0][k - cnt1] + 1);
}
}
}
int ans = 0;
for (auto& row : f) {
ans = max(ans, ranges::max(row));
}
return ans;
}
};
func findMaxForm(strs []string, m, n int) (ans int) {
f := make([][]int, m+1)
for i := range f {
f[i] = make([]int, n+1)
}
sum0, sum1 := 0, 0
for _, s := range strs {
cnt0 := strings.Count(s, "0")
cnt1 := len(s) - cnt0
sum0 = min(sum0+cnt0, m)
sum1 = min(sum1+cnt1, n)
for j := sum0; j >= cnt0; j-- {
for k := sum1; k >= cnt1; k-- {
f[j][k] = max(f[j][k], f[j-cnt0][k-cnt1]+1)
}
}
}
for _, row := range f {
ans = max(ans, slices.Max(row))
}
return
}
复杂度分析
- 时间复杂度:$\mathcal{O}(kmn+L)$,其中 $k$ 为 $\textit{strs}$ 的长度,$L$ 为 $\textit{strs}$ 中所有字符串的长度之和。
- 空间复杂度:$\mathcal{O}(mn)$。
更多相似题目,见 动态规划题单 中的「§3.1 0-1 背包」。
分类题单
如何科学刷题?
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 二分算法(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/最短路/最小生成树/二分图/基环树/欧拉路径)
- 【本题相关】动态规划(入门/背包/状态机/划分/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、二叉树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA/一般树)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)
我的题解精选(已分类)
欢迎关注 B站@灵茶山艾府

 {:width=400}
{:width=400}