给你一个二进制数组 nums ，你需要从中删掉一个元素。
请你在删掉元素的结果数组中，返回最长的且只包含 1 的非空子数组的长度。
如果不存在这样的子数组，请返回 0 。
提示 1：
输入：nums = [1,1,0,1] 输出：3 解释：删掉位置 2 的数后，[1,1,1] 包含 3 个 1 。
示例 2：
输入：nums = [0,1,1,1,0,1,1,0,1] 输出：5 解释：删掉位置 4 的数字后，[0,1,1,1,1,1,0,1] 的最长全 1 子数组为 [1,1,1,1,1] 。
示例 3：
输入：nums = [1,1,1] 输出：2 解释：你必须要删除一个元素。
提示：
登录1 <= nums.length <= 105nums[i] 要么是 0 要么是 1 。删除后，子数组只有 $1$，也就是没有 $0$。那么删除之前呢？至多有一个 $0$。
所以问题相当于：
子数组越短，包含的 $0$ 越少，越能满足要求；子数组越长，包含的 $0$ 越多，越无法满足要求。所以当子数组的右端点增大时，左端点也随之增大（或者不变），这符合滑动窗口模型。如果你不了解滑动窗口，请看视频【基础算法精讲 03】。
这个方法对于至多有 $k$ 个 $0$ 的题目，也是适用的。
⚠注意：删除之前的子数组长度是 $\textit{right}-\textit{left}+1$，由于题目一定要删除一个数（尤其是在全为 $1$ 的情况下，一定要删除一个 $1$），所以删除后的子数组长度是 $\textit{right}-\textit{left}$，用其更新答案的最大值。
###py
class Solution:
def longestSubarray(self, nums: List[int]) -> int:
ans = cnt0 = left = 0
for right, x in enumerate(nums):
# 1. 入，nums[right] 进入窗口
cnt0 += 1 - x # 维护窗口中的 0 的个数
while cnt0 > 1: # 不符合题目要求
# 2. 出，nums[left] 离开窗口
cnt0 -= 1 - nums[left] # 维护窗口中的 0 的个数
left += 1
# 3. 更新答案，注意不是 right-left+1，因为我们要删掉一个数
ans = max(ans, right - left)
return ans
###java
class Solution {
public int longestSubarray(int[] nums) {
int ans = 0;
int cnt0 = 0;
int left = 0;
for (int right = 0; right < nums.length; right++) {
// 1. 入，nums[right] 进入窗口
cnt0 += 1 - nums[right]; // 维护窗口中的 0 的个数
while (cnt0 > 1) { // 不符合题目要求
// 2. 出，nums[left] 离开窗口
cnt0 -= 1 - nums[left]; // 维护窗口中的 0 的个数
left++;
}
// 3. 更新答案，注意不是 right-left+1，因为我们要删掉一个数
ans = Math.max(ans, right - left);
}
return ans;
}
}
###cpp
class Solution {
public:
int longestSubarray(vector<int>& nums) {
int ans = 0, cnt0 = 0, left = 0;
for (int right = 0; right < nums.size(); right++) {
// 1. 入，nums[right] 进入窗口
cnt0 += 1 - nums[right]; // 维护窗口中的 0 的个数
while (cnt0 > 1) { // 不符合题目要求
// 2. 出，nums[left] 离开窗口
cnt0 -= 1 - nums[left]; // 维护窗口中的 0 的个数
left++;
}
// 3. 更新答案，注意不是 right-left+1，因为我们要删掉一个数
ans = max(ans, right - left);
}
return ans;
}
};
###c
#define MAX(a, b) ((b) > (a) ? (b) : (a))
int longestSubarray(int* nums, int numsSize) {
int ans = 0, cnt0 = 0, left = 0;
for (int right = 0; right < numsSize; right++) {
// 1. 入，nums[right] 进入窗口
cnt0 += 1 - nums[right]; // 维护窗口中的 0 的个数
while (cnt0 > 1) { // 不符合题目要求
// 2. 出，nums[left] 离开窗口
cnt0 -= 1 - nums[left]; // 维护窗口中的 0 的个数
left++;
}
// 3. 更新答案，注意不是 right-left+1，因为我们要删掉一个数
ans = MAX(ans, right - left);
}
return ans;
}
###go
func longestSubarray(nums []int) (ans int) {
cnt0, left := 0, 0
for right, x := range nums {
// 1. 入，nums[right] 进入窗口
cnt0 += 1 - x // 维护窗口中的 0 的个数
for cnt0 > 1 { // 不符合题目要求
// 2. 出，nums[left] 离开窗口
cnt0 -= 1 - nums[left] // 维护窗口中的 0 的个数
left++
}
// 3. 更新答案，注意不是 right-left+1，因为我们要删掉一个数
ans = max(ans, right-left)
}
return
}
###js
var longestSubarray = function(nums) {
let ans = 0, cnt0 = 0, left = 0;
for (let right = 0; right < nums.length; right++) {
// 1. 入，nums[right] 进入窗口
cnt0 += 1 - nums[right]; // 维护窗口中的 0 的个数
while (cnt0 > 1) { // 不符合题目要求
// 2. 出，nums[left] 离开窗口
cnt0 -= 1 - nums[left]; // 维护窗口中的 0 的个数
left++;
}
// 3. 更新答案，注意不是 right-left+1，因为我们要删掉一个数
ans = Math.max(ans, right - left);
}
return ans;
};
###rust
impl Solution {
pub fn longest_subarray(nums: Vec<i32>) -> i32 {
let mut ans = 0;
let mut cnt0 = 0;
let mut left = 0;
for (right, &x) in nums.iter().enumerate() {
// 1. 入，nums[right] 进入窗口
cnt0 += 1 - x; // 维护窗口中的 0 的个数
while cnt0 > 1 {
// 2. 出，nums[left] 离开窗口
cnt0 -= 1 - nums[left]; // 维护窗口中的 0 的个数
left += 1;
}
// 3. 更新答案，注意不是 right-left+1，因为我们要删掉一个数
ans = ans.max(right - left);
}
ans as _
}
}
见下面滑动窗口题单的「§2.1 越短越合法/求最长/最大」。
欢迎关注 B站@灵茶山艾府
思路
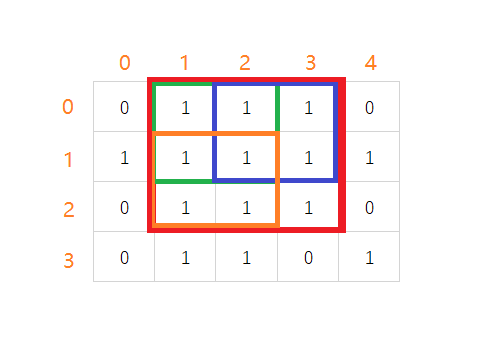
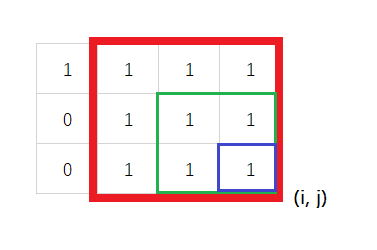
在删掉元素的结果数组中，最长的且只包含 $1$ 的非空子数组存在两种情况：
这个子数组在原数组中本身就是连续的，无论删或者不删其他的元素，它都是最长的且只包含 $1$ 的非空子数组；
这个子数组原本不连续，而是两个连续的全 $1$ 子数组，中间夹着一个 $0$，把这个 $0$ 删掉以后，左右两个子数组组合成一个最长的且只包含 $1$ 的非空子数组。
我们可以枚举被删除的位置，假设下标为 $i$，我们希望知道「以第 $i - 1$ 位结尾的最长连续全 $1$ 子数组」和「以第 $i + 1$ 位开头的最长连续全 $1$ 子数组」的长度分别是多少，这两个量的和就是删除第 $i$ 位之后最长的且只包含 $1$ 的非空子数组的长度。假设我们可以得到这两个量，我们只要枚举所有的 $i$，就可以得到最终的答案。
我们可以这样维护「以第 $i - 1$ 位结尾的最长连续全 $1$ 子数组」和「以第 $i + 1$ 位开头的最长连续全 $1$ 子数组」的长度：
记原数组为 $a$
记 ${\rm pre}(i)$ 为「以第 $i$ 位结尾的最长连续全 $1$ 子数组」，那么
$$
{\rm pre}(i) = \left{ \begin{aligned}
& 0 , & a_i = 0 \
& {\rm pre}(i - 1) + 1 , & a_i = 1
\end{aligned} \right.
$$
记 ${\rm suf}(i)$ 为「以第 $i$ 位开头的最长连续全 $1$ 子数组」，那么
$$
{\rm suf}(i) = \left{ \begin{aligned}
& 0 , & a_i = 0 \
& {\rm suf}(i + 1) + 1 , & a_i = 1
\end{aligned} \right.
$$
我们可以对原数组做一次正向遍历，预处理出 $\rm pre$，再做一次反向遍历，预处理出 $\rm suf$。最后我们枚举所有的元素作为待删除的元素，计算出删除这些元素之后最长的且只包含 $1$ 的非空子数组的长度，比较并取最大值。
代码如下。
算法
###C++
class Solution {
public:
int longestSubarray(vector<int>& nums) {
int n = nums.size();
vector<int> pre(n), suf(n);
pre[0] = nums[0];
for (int i = 1; i < n; ++i) {
pre[i] = nums[i] ? pre[i - 1] + 1 : 0;
}
suf[n - 1] = nums[n - 1];
for (int i = n - 2; i >= 0; --i) {
suf[i] = nums[i] ? suf[i + 1] + 1 : 0;
}
int ans = 0;
for (int i = 0; i < n; ++i) {
int preSum = i == 0 ? 0 : pre[i - 1];
int sufSum = i == n - 1 ? 0 : suf[i + 1];
ans = max(ans, preSum + sufSum);
}
return ans;
}
};
###Java
class Solution {
public int longestSubarray(int[] nums) {
int n = nums.length;
int[] pre = new int[n];
int[] suf = new int[n];
pre[0] = nums[0];
for (int i = 1; i < n; ++i) {
pre[i] = nums[i] != 0 ? pre[i - 1] + 1 : 0;
}
suf[n - 1] = nums[n - 1];
for (int i = n - 2; i >= 0; --i) {
suf[i] = nums[i] != 0 ? suf[i + 1] + 1 : 0;
}
int ans = 0;
for (int i = 0; i < n; ++i) {
int preSum = i == 0 ? 0 : pre[i - 1];
int sufSum = i == n - 1 ? 0 : suf[i + 1];
ans = Math.max(ans, preSum + sufSum);
}
return ans;
}
}
###Python
class Solution:
def longestSubarray(self, nums: List[int]) -> int:
n = len(nums)
pre = [0] * n
suf = [0] * n
pre[0] = nums[0]
for i in range(1, n):
pre[i] = pre[i - 1] + 1 if nums[i] else 0
suf[-1] = nums[-1]
for i in range(n - 2, -1, -1):
suf[i] = suf[i + 1] + 1 if nums[i] else 0
ans = 0
for i in range(n):
pre_sum = pre[i - 1] if i > 0 else 0
suf_sum = suf[i + 1] if i < n - 1 else 0
ans = max(ans, pre_sum + suf_sum)
return ans
###C#
public class Solution {
public int LongestSubarray(int[] nums) {
int n = nums.Length;
int[] pre = new int[n];
int[] suf = new int[n];
pre[0] = nums[0];
for (int i = 1; i < n; ++i) {
pre[i] = nums[i] != 0 ? pre[i - 1] + 1 : 0;
}
suf[n - 1] = nums[n - 1];
for (int i = n - 2; i >= 0; --i) {
suf[i] = nums[i] != 0 ? suf[i + 1] + 1 : 0;
}
int ans = 0;
for (int i = 0; i < n; ++i) {
int preSum = i == 0 ? 0 : pre[i - 1];
int sufSum = i == n - 1 ? 0 : suf[i + 1];
ans = Math.Max(ans, preSum + sufSum);
}
return ans;
}
}
###Go
func longestSubarray(nums []int) int {
n := len(nums)
pre := make([]int, n)
suf := make([]int, n)
pre[0] = nums[0]
for i := 1; i < n; i++ {
if nums[i] != 0 {
pre[i] = pre[i - 1] + 1
} else {
pre[i] = 0
}
}
suf[n - 1] = nums[n - 1]
for i := n - 2; i >= 0; i-- {
if nums[i] != 0 {
suf[i] = suf[i + 1] + 1
} else {
suf[i] = 0
}
}
ans := 0
for i := 0; i < n; i++ {
preSum := 0
if i != 0 {
preSum = pre[i - 1]
}
sufSum := 0
if i != n - 1 {
sufSum = suf[i + 1]
}
if preSum + sufSum > ans {
ans = preSum + sufSum
}
}
return ans
}
###C
int longestSubarray(int* nums, int numsSize) {
int* pre = (int*)malloc(numsSize * sizeof(int));
int* suf = (int*)malloc(numsSize * sizeof(int));
pre[0] = nums[0];
for (int i = 1; i < numsSize; ++i) {
pre[i] = nums[i] ? pre[i - 1] + 1 : 0;
}
suf[numsSize - 1] = nums[numsSize - 1];
for (int i = numsSize - 2; i >= 0; --i) {
suf[i] = nums[i] ? suf[i + 1] + 1 : 0;
}
int ans = 0;
for (int i = 0; i < numsSize; ++i) {
int preSum = i == 0 ? 0 : pre[i - 1];
int sufSum = i == numsSize - 1 ? 0 : suf[i + 1];
ans = fmax(ans, preSum + sufSum);
}
free(pre);
free(suf);
return ans;
}
###JavaScript
var longestSubarray = function(nums) {
const n = nums.length;
const pre = new Array(n);
const suf = new Array(n);
pre[0] = nums[0];
for (let i = 1; i < n; ++i) {
pre[i] = nums[i] ? pre[i - 1] + 1 : 0;
}
suf[n - 1] = nums[n - 1];
for (let i = n - 2; i >= 0; --i) {
suf[i] = nums[i] ? suf[i + 1] + 1 : 0;
}
let ans = 0;
for (let i = 0; i < n; ++i) {
const preSum = i === 0 ? 0 : pre[i - 1];
const sufSum = i === n - 1 ? 0 : suf[i + 1];
ans = Math.max(ans, preSum + sufSum);
}
return ans;
};
###TypeScript
function longestSubarray(nums: number[]): number {
const n = nums.length;
const pre: number[] = new Array(n);
const suf: number[] = new Array(n);
pre[0] = nums[0];
for (let i = 1; i < n; ++i) {
pre[i] = nums[i] ? pre[i - 1] + 1 : 0;
}
suf[n - 1] = nums[n - 1];
for (let i = n - 2; i >= 0; --i) {
suf[i] = nums[i] ? suf[i + 1] + 1 : 0;
}
let ans = 0;
for (let i = 0; i < n; ++i) {
const preSum = i === 0 ? 0 : pre[i - 1];
const sufSum = i === n - 1 ? 0 : suf[i + 1];
ans = Math.max(ans, preSum + sufSum);
}
return ans;
}
###Rust
impl Solution {
pub fn longest_subarray(nums: Vec<i32>) -> i32 {
let n = nums.len();
let mut pre = vec![0; n];
let mut suf = vec![0; n];
pre[0] = nums[0];
for i in 1..n {
pre[i] = if nums[i] != 0 { pre[i - 1] + 1 } else { 0 };
}
suf[n - 1] = nums[n - 1];
for i in (0..n - 1).rev() {
suf[i] = if nums[i] != 0 { suf[i + 1] + 1 } else { 0 };
}
let mut ans = 0;
for i in 0..n {
let pre_sum = if i == 0 { 0 } else { pre[i - 1] };
let suf_sum = if i == n - 1 { 0 } else { suf[i + 1] };
ans = ans.max(pre_sum + suf_sum);
}
ans
}
}
复杂度
假设原数组长度为 $n$。
时间复杂度：$O(n)$。这里对原数组进行三次遍历，每次时间代价为 $O(n)$，故渐进时间复杂度为 $O(n)$。
空间复杂度：$O(n)$。这里预处理 $\rm pre$ 和 $\rm suf$ 需要两个长度为 $n$ 的数组。
思路
我们也可以修改递推的方式使用一次就可以得到答案。
记 $p_0(i)$ 为「以第 $i$ 位结尾的最长连续全 $1$ 子数组」，与方法一中的 ${\rm pre}(i)$ 相同，递推式为：
$$
p_0(i) = \left{ \begin{aligned}
& 0 , & a_i = 0 \
& p_0(i - 1) + 1 , & a_i = 1
\end{aligned} \right.
$$
同时，我们记 $p_1(i)$ 为「以第 $i$ 位结尾，并且可以在某个位置删除一个 $0$ 的最长连续全 $1$ 子数组」。注意这里我们规定了只删除 $0$，而不是任意一个元素，这是因为只要数组中的元素不全为 $1$，那么删除 $1$ 就没有任何意义。$p_1(i)$ 的递推式为：
$$
p_1(i) = \left{ \begin{aligned}
& p_0(i - 1) , & a_i = 0 \
& p_1(i - 1) + 1 , & a_i = 1
\end{aligned} \right.
$$
当我们遇到 $1$ 时，$p_1(i)$ 的递推式与 $p_0(i)$ 相同；而当我们遇到 $0$ 时，由于 $p_1(i)$ 允许删除一个 $0$，那么我们可以把这个 $0$ 删除，将 $p_0(i-1)$ 的值赋予 $p_1(i)$。
最后的答案即为 $p_1(i)$ 中的最大值。当遇到数组中的元素全为 $1$ 的特殊情况时，我们需要将答案减去 $1$，这是因为在这种情况下，我们不得不删除一个 $1$。注意到递推式中所有的 $p_0(i), p_1(i)$ 只和 $p_0(i-1), p_1(i-1)$ 相关，因此我们可以直接使用两个变量进行递推，减少空间复杂度。
算法
###C++
class Solution {
public:
int longestSubarray(vector<int>& nums) {
int ans = 0;
int p0 = 0, p1 = 0;
for (int num: nums) {
if (num == 0) {
p1 = p0;
p0 = 0;
}
else {
++p0;
++p1;
}
ans = max(ans, p1);
}
if (ans == nums.size()) {
--ans;
}
return ans;
}
};
###Java
class Solution {
public int longestSubarray(int[] nums) {
int ans = 0;
int p0 = 0, p1 = 0;
for (int num : nums) {
if (num == 0) {
p1 = p0;
p0 = 0;
} else {
++p0;
++p1;
}
ans = Math.max(ans, p1);
}
if (ans == nums.length) {
--ans;
}
return ans;
}
}
###Python
class Solution:
def longestSubarray(self, nums: List[int]) -> int:
ans = 0
p0 = p1 = 0
for num in nums:
if num == 0:
p1, p0 = p0, 0
else:
p0 += 1
p1 += 1
ans = max(ans, p1)
if ans == len(nums):
ans -= 1
return ans
###C#
public class Solution {
public int LongestSubarray(int[] nums) {
int ans = 0;
int p0 = 0, p1 = 0;
foreach (int num in nums) {
if (num == 0) {
p1 = p0;
p0 = 0;
}
else {
++p0;
++p1;
}
ans = Math.Max(ans, p1);
}
if (ans == nums.Length) {
--ans;
}
return ans;
}
}
###Go
func longestSubarray(nums []int) int {
ans := 0
p0, p1 := 0, 0
for _, num := range nums {
if num == 0 {
p1 = p0
p0 = 0
} else {
p0++
p1++
}
if p1 > ans {
ans = p1
}
}
if ans == len(nums) {
ans--
}
return ans
}
###C
int longestSubarray(int* nums, int numsSize) {
int ans = 0;
int p0 = 0, p1 = 0;
for (int i = 0; i < numsSize; i++) {
if (nums[i] == 0) {
p1 = p0;
p0 = 0;
} else {
++p0;
++p1;
}
ans = fmax(ans, p1);
}
if (ans == numsSize) {
--ans;
}
return ans;
}
###JavaScript
var longestSubarray = function(nums) {
let ans = 0;
let p0 = 0, p1 = 0;
for (const num of nums) {
if (num === 0) {
p1 = p0;
p0 = 0;
} else {
p0++;
p1++;
}
ans = Math.max(ans, p1);
}
if (ans === nums.length) {
ans--;
}
return ans;
};
###TypeScript
function longestSubarray(nums: number[]): number {
let ans = 0;
let p0 = 0, p1 = 0;
for (const num of nums) {
if (num === 0) {
p1 = p0;
p0 = 0;
} else {
p0++;
p1++;
}
ans = Math.max(ans, p1);
}
if (ans === nums.length) {
ans--;
}
return ans;
}
###Rust
impl Solution {
pub fn longest_subarray(nums: Vec<i32>) -> i32 {
let mut ans = 0;
let mut p0 = 0;
let mut p1 = 0;
for &num in nums.iter() {
if num == 0 {
p1 = p0;
p0 = 0;
} else {
p0 += 1;
p1 += 1;
}
ans = ans.max(p1);
}
if ans == nums.len() as i32 {
ans -= 1;
}
ans
}
}
复杂度
假设原数组长度为 $n$。
时间复杂度：$O(n)$。这里对原数组进行一次遍历，时间代价为 $O(n)$，故渐进时间复杂度为 $O(n)$。
空间复杂度：$O(1)$。
a 存中间有一个“非1”的和，b 存连续1的和，遇 1 两数自增，遇“非1” a=b;b=0。
扫描过程保存最大的 a 值，最后处理一下全1特例即可。
class Solution {
public int longestSubarray(int[] nums) {
int ret = 0;
int a = 0;
int b = 0;
int n = nums.length;
for (int i = 0; i < n; ++i) {
if (nums[i] == 1) {
++a;
++b;
ret = Math.max(ret, a);
} else {
a = b;
b = 0;
}
}
if (ret == n) ret--;
return ret;
}
}
我们可以遍历 grid，找到所有 1 的最小边界，记为 $(x_1, y_1)$，最大边界，记为 $(x_2, y_2)$，那么最小矩形的面积就是 $(x_2 - x_1 + 1) \times (y_2 - y_1 + 1)$。
###python
class Solution:
def minimumArea(self, grid: List[List[int]]) -> int:
x1 = y1 = inf
x2 = y2 = -inf
for i, row in enumerate(grid):
for j, x in enumerate(row):
if x == 1:
x1 = min(x1, i)
y1 = min(y1, j)
x2 = max(x2, i)
y2 = max(y2, j)
return (x2 - x1 + 1) * (y2 - y1 + 1)
###java
class Solution {
public int minimumArea(int[][] grid) {
int m = grid.length, n = grid[0].length;
int x1 = m, y1 = n;
int x2 = 0, y2 = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
x1 = Math.min(x1, i);
y1 = Math.min(y1, j);
x2 = Math.max(x2, i);
y2 = Math.max(y2, j);
}
}
}
return (x2 - x1 + 1) * (y2 - y1 + 1);
}
}
###cpp
class Solution {
public:
int minimumArea(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int x1 = m, y1 = n;
int x2 = 0, y2 = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
x1 = min(x1, i);
y1 = min(y1, j);
x2 = max(x2, i);
y2 = max(y2, j);
}
}
}
return (x2 - x1 + 1) * (y2 - y1 + 1);
}
};
###go
func minimumArea(grid [][]int) int {
x1, y1 := len(grid), len(grid[0])
x2, y2 := 0, 0
for i, row := range grid {
for j, x := range row {
if x == 1 {
x1, y1 = min(x1, i), min(y1, j)
x2, y2 = max(x2, i), max(y2, j)
}
}
}
return (x2 - x1 + 1) * (y2 - y1 + 1)
}
###ts
function minimumArea(grid: number[][]): number {
const [m, n] = [grid.length, grid[0].length];
let [x1, y1] = [m, n];
let [x2, y2] = [0, 0];
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid[i][j] === 1) {
x1 = Math.min(x1, i);
y1 = Math.min(y1, j);
x2 = Math.max(x2, i);
y2 = Math.max(y2, j);
}
}
}
return (x2 - x1 + 1) * (y2 - y1 + 1);
}
时间复杂度 $O(m \times n)$，其中 $m$ 和 $n$ 分别是 grid 的行数和列数。空间复杂度 $O(1)$。
有任何问题，欢迎评论区交流，欢迎评论区提供其它解题思路（代码），也可以点个赞支持一下作者哈😄~
给你一个二维 二进制 数组 grid。请你找出一个边在水平方向和竖直方向上、面积 最小 的矩形，并且满足 grid 中所有的 1 都在矩形的内部。
返回这个矩形可能的 最小 面积。
示例 1：
输入： grid = [[0,1,0],[1,0,1]]
输出： 6
解释：
这个最小矩形的高度为 2，宽度为 3，因此面积为 2 * 3 = 6。
示例 2：
输入： grid = [[0,0],[1,0]]
输出： 1
解释：
这个最小矩形的高度和宽度都是 1，因此面积为 1 * 1 = 1。
提示：
1 <= grid.length, grid[i].length <= 1000grid[i][j] 是 0 或 1。grid 中至少有一个 1 。经典题。求包含所有点的，边与坐标轴平行的矩形的最小面积。
矩形的上（下）边界即为所有点中纵坐标最大（小）的，矩形的左（右）边界即为所有点中横坐标最大（小）的。枚举所有点计算边界即可。复杂度 $\mathcal{O}(nm)$。
###cpp
class Solution {
public:
int minimumArea(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
int U = n, D = -1, L = m, R = -1;
for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) if (grid[i][j]) {
U = min(U, i); D = max(D, i);
L = min(L, j); R = max(R, j);
}
return (D - U + 1) * (R - L + 1);
}
};
遍历 $\textit{grid}$：
矩形面积至少为
$$
(\textit{right} - \textit{left} + 1) \cdot (\textit{bottom} - \textit{top} + 1)
$$
###py
class Solution:
def minimumArea(self, grid: List[List[int]]) -> int:
left = top = inf
right = bottom = 0
for i, row in enumerate(grid):
for j, x in enumerate(row):
if x:
left = min(left, j)
right = max(right, j)
top = min(top, i)
bottom = i
return (right - left + 1) * (bottom - top + 1)
###java
class Solution {
public int minimumArea(int[][] grid) {
int left = Integer.MAX_VALUE;
int right = 0;
int top = Integer.MAX_VALUE;
int bottom = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[i].length; j++) {
if (grid[i][j] == 1) {
left = Math.min(left, j);
right = Math.max(right, j);
top = Math.min(top, i);
bottom = i;
}
}
}
return (right - left + 1) * (bottom - top + 1);
}
}
###cpp
class Solution {
public:
int minimumArea(vector<vector<int>>& grid) {
int left = INT_MAX, right = 0;
int top = INT_MAX, bottom = 0;
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[i].size(); j++) {
if (grid[i][j]) {
left = min(left, j);
right = max(right, j);
top = min(top, i);
bottom = i;
}
}
}
return (right - left + 1) * (bottom - top + 1);
}
};
###c
#define MIN(a, b) ((b) < (a) ? (b) : (a))
#define MAX(a, b) ((b) > (a) ? (b) : (a))
int minimumArea(int** grid, int gridSize, int* gridColSize) {
int left = INT_MAX, right = 0;
int top = INT_MAX, bottom = 0;
for (int i = 0; i < gridSize; i++) {
for (int j = 0; j < gridColSize[i]; j++) {
if (grid[i][j]) {
left = MIN(left, j);
right = MAX(right, j);
top = MIN(top, i);
bottom = i;
}
}
}
return (right - left + 1) * (bottom - top + 1);
}
###go
func minimumArea(grid [][]int) int {
left, right := math.MaxInt, 0
top, bottom := math.MaxInt, 0
for i, row := range grid {
for j, x := range row {
if x == 1 {
left = min(left, j)
right = max(right, j)
top = min(top, i)
bottom = i
}
}
}
return (right - left + 1) * (bottom - top + 1)
}
###js
var minimumArea = function(grid) {
let left = Infinity, right = 0;
let top = Infinity, bottom = 0;
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[i].length; j++) {
if (grid[i][j]) {
left = Math.min(left, j);
right = Math.max(right, j);
top = Math.min(top, i);
bottom = i;
}
}
}
return (right - left + 1) * (bottom - top + 1);
};
###rust
impl Solution {
pub fn minimum_area(grid: Vec<Vec<i32>>) -> i32 {
let mut left = usize::MAX;
let mut right = 0;
let mut top = usize::MAX;
let mut bottom = 0;
for (i, row) in grid.into_iter().enumerate() {
for (j, x) in row.into_iter().enumerate() {
if x != 0 {
left = left.min(j);
right = right.max(j);
top = top.min(i);
bottom = i;
}
}
}
((right - left + 1) * (bottom - top + 1)) as _
}
}
欢迎关注 B站@灵茶山艾府
给你一个 m x n 的二进制矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。
示例 1：
输入：mat = [[1,0,1],[1,1,0],[1,1,0]] 输出：13 解释： 有 6 个 1x1 的矩形。 有 2 个 1x2 的矩形。 有 3 个 2x1 的矩形。 有 1 个 2x2 的矩形。 有 1 个 3x1 的矩形。 矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
示例 2：
输入：mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] 输出：24 解释： 有 8 个 1x1 的子矩形。 有 5 个 1x2 的子矩形。 有 2 个 1x3 的子矩形。 有 4 个 2x1 的子矩形。 有 2 个 2x2 的子矩形。 有 2 个 3x1 的子矩形。 有 1 个 3x2 的子矩形。 矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。
提示：
1 <= m, n <= 150mat[i][j] 仅包含 0 或 1
枚举子矩形的上下边界，统计每一列的 $1$ 的个数，把原问题「压缩」为一维数组上的问题。
在示例 2 中，假设现在枚举到子矩形的上边界为 $0$ 行，下边界为 $1$ 行，即 $\textit{mat}$ 的前两行。子矩形的高 $h=2$。
统计每一列的 $1$ 的个数，得到一个一维数组 $a=[0,2,2,1]$。我们要找的子矩形，就是 $a$ 的子数组。由于全 $1$ 子矩形的每一列都是 $1$，所以子数组的每一项都得是子矩形的高 $h=2$。问题变成：
做法同 2348. 全 0 子数组的数目。
代码实现时，外层循环枚举上边界，内层循环枚举下边界。当下边界 $\textit{bottom}$ 加一时，只需把每个 $a[j]$ 都增加相应的 $\textit{mat}[\textit{bottom}][j]$，无需整个重新统计。
###py
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
ans = 0
for top in range(m): # 枚举上边界
a = [0] * n
for bottom in range(top, m): # 枚举下边界
h = bottom - top + 1 # 高
# 2348. 全 h 子数组的数目
last = -1
for j in range(n):
a[j] += mat[bottom][j] # 把 bottom 这一行的值加到 a 中
if a[j] != h:
last = j # 记录上一个非 h 元素的位置
else:
ans += j - last
return ans
###java
class Solution {
public int numSubmat(int[][] mat) {
int m = mat.length;
int n = mat[0].length;
int ans = 0;
for (int top = 0; top < m; top++) { // 枚举上边界
int[] a = new int[n];
for (int bottom = top; bottom < m; bottom++) { // 枚举下边界
int h = bottom - top + 1; // 高
// 2348. 全 h 子数组的数目
int last = -1;
for (int j = 0; j < n; j++) {
a[j] += mat[bottom][j]; // 把 bottom 这一行的值加到 a 中
if (a[j] != h) {
last = j; // 记录上一个非 h 元素的位置
} else {
ans += j - last;
}
}
}
}
return ans;
}
}
###cpp
class Solution {
public:
int numSubmat(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
int ans = 0;
for (int top = 0; top < m; top++) { // 枚举上边界
vector<int> a(n);
for (int bottom = top; bottom < m; bottom++) { // 枚举下边界
int h = bottom - top + 1; // 高
// 2348. 全 h 子数组的数目
int last = -1;
for (int j = 0; j < n; j++) {
a[j] += mat[bottom][j]; // 把 bottom 这一行的值加到 a 中
if (a[j] != h) {
last = j; // 记录上一个非 h 元素的位置
} else {
ans += j - last;
}
}
}
}
return ans;
}
};
###go
func numSubmat(mat [][]int) (ans int) {
m, n := len(mat), len(mat[0])
for top := range m { // 枚举上边界
a := make([]int, n)
for bottom := top; bottom < m; bottom++ { // 枚举下边界
h := bottom - top + 1 // 高
// 2348. 全 h 子数组的数目
last := -1
for j := range n {
a[j] += mat[bottom][j] // 把 bottom 这一行的值加到 a 中
if a[j] != h {
last = j // 记录上一个非 h 元素的位置
} else {
ans += j - last
}
}
}
}
return
}
枚举子矩形的右下角（枚举底边，枚举右边界），有多少个对应的子矩形？
举个例子。
在示例 2 中，当我们枚举到最后一行时，柱子高度为 $\textit{heights}=[1,3,3,0]$。然后枚举子矩形的右边界：
一般地，用 单调栈 计算小于 $\textit{heights}[j]$ 的左边最近柱子的位置 $\textit{left}$，把子矩形分成两类：
###py
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
heights = [0] * len(mat[0])
ans = 0
for row in mat:
for j, x in enumerate(row):
if x == 0:
heights[j] = 0
else:
heights[j] += 1
# (j, f, heights[j])
st = [(-1, 0, -1)] # 哨兵，方便处理 left=-1 的情况
for j, h in enumerate(heights):
while st[-1][2] >= h:
st.pop()
left, f, _ = st[-1]
# 计算底边为 row，右边界为 j 的子矩形个数
# 左边界 <= left 的矩形，每个矩形的右边界都可以扩展到 j，一共有 f 个
# 左边界 > left 的矩形，左边界有 j-left 种，高度有 h 种，一共有 (j-left)*h 个
f += (j - left) * h
ans += f
st.append((j, f, h))
return ans
###java
class Solution {
public int numSubmat(int[][] mat) {
int n = mat[0].length;
int[] heights = new int[n];
int ans = 0;
int[][] st = new int[n + 1][3]; // (j, f, heights[j])
for (int[] row : mat) {
for (int j = 0; j < n; j++) {
if (row[j] == 0) {
heights[j] = 0;
} else {
heights[j]++;
}
}
st[0][0] = st[0][2] = -1; // 哨兵，方便处理 left=-1 的情况
int top = 0;
for (int j = 0; j < n; j++) {
int h = heights[j];
while (st[top][2] >= h) {
top--; // 出栈
}
int left = st[top][0];
int f = st[top][1];
// 计算底边为 row，右边界为 j 的子矩形个数
// 左边界 <= left 的矩形，每个矩形的右边界都可以扩展到 j，一共有 f 个
// 左边界 > left 的矩形，左边界有 j-left 种，高度有 h 种，一共有 (j-left)*h 个
f += (j - left) * h;
ans += f;
top++;
st[top][0] = j; // 入栈
st[top][1] = f;
st[top][2] = h;
}
}
return ans;
}
}
###cpp
class Solution {
public:
int numSubmat(vector<vector<int>>& mat) {
int n = mat[0].size();
vector<int> heights(n);
int ans = 0;
for (auto& row : mat) {
for (int j = 0; j < n; j++) {
if (row[j] == 0) {
heights[j] = 0;
} else {
heights[j]++;
}
}
stack<tuple<int, int, int>> st; // (j, f, heights[j])
st.emplace(-1, 0, -1); // 哨兵，方便处理 left=-1 的情况
for (int j = 0; j < n; j++) {
int h = heights[j];
while (get<2>(st.top()) >= h) {
st.pop();
}
auto [left, f, _] = st.top();
// 计算底边为 row，右边界为 j 的子矩形个数
// 左边界 <= left 的矩形，每个矩形的右边界都可以扩展到 j，一共有 f 个
// 左边界 > left 的矩形，左边界有 j-left 种，高度有 h 种，一共有 (j-left)*h 个
f += (j - left) * h;
ans += f;
st.emplace(j, f, h);
}
}
return ans;
}
};
###go
func numSubmat(mat [][]int) (ans int) {
heights := make([]int, len(mat[0]))
for _, row := range mat {
for j, x := range row {
if x == 0 {
heights[j] = 0
} else {
heights[j]++
}
}
type tuple struct{ j, f, h int }
st := []tuple{{-1, 0, -1}} // 哨兵，方便处理 left=-1 的情况
for j, h := range heights {
for st[len(st)-1].h >= h {
st = st[:len(st)-1]
}
p := st[len(st)-1]
left, f := p.j, p.f
// 计算底边为 row，右边界为 j 的子矩形个数
// 左边界 <= left 的矩形，每个矩形的右边界都可以扩展到 j，一共有 f 个
// 左边界 > left 的矩形，左边界有 j-left 种，高度有 h 种，一共有 (j-left)*h 个
f += (j - left) * h
ans += f
st = append(st, tuple{j, f, h})
}
}
return
}
见下面单调栈题单的「二、矩形」。
欢迎关注 B站@灵茶山艾府
看了很多题解，大家大致的思路基本一致，时间复杂度为O(n·n·m)，但大多题解没有把过程表述的很完整，作为一个刷题的小白，我想在这写写小白也能看懂的思路，和做这道题的一些细节和收获
题目要求既要考虑1x2, 2x1的情况, 也要考虑2x2的情况：
(1)先考虑1xn的情况，即在一行中(横向)可以找出多少个矩形**(这步我称之为"统计")**，代码如下：统计行中的矩形数目 int now = 0; for (int k = 0; k < col; k++){ if (mat[j][k] == 0) now = 0; else now = k == 0 ? mat[j][0] : now + 1; ans += now; }
(2)压缩：
起始的二维数组
对其使用“按位与”进行压缩
第二次统计的结果
思考：这里我们可以发现第二次的统计是2xn的，既包含了2X1的情况也包含了2x2的情况，接下来的步骤继续如上循环"压缩"即可
###java
class Solution {
public int numSubmat(int[][] mat) {
int row = mat.length, col = mat[0].length, ans = 0;
for (int i = 0; i < row; i++){
//统计
for (int j = i; j < row; j++){
int now = 0;
for (int k = 0; k < col; k++){
if (mat[j][k] == 0) now = 0;
else now = k == 0 ? mat[j][0] : now + 1;
ans += now;
}
}
//压缩
for (int j = row - 1; j > i; j--){
for (int k = 0; k < col; k++){
mat[j][k] = mat[j][k] & mat[j - 1][k];
}
}
}
return ans;
}
}
希望这篇题解能让你看懂，喜欢的留下你宝贵的会心一赞吧，刷题之路，我们绝不言败！ヾ(◍°∇°◍)ﾉﾞ
矩阵里每个点(i.j)统计他这行左边到他这个位置最多有几个连续的1，存为left[i][j]。然后对于每个点(i.j)，我们固定子矩形的右下角为(i.j)，利用left从该行i向上寻找子矩阵左上角为第k行的矩阵个数。每次将子矩阵个数加到答案中即可。
时间复杂度O(nnm)，空间复杂度O(nm)。
###cpp
class Solution {
public:
int numSubmat(vector<vector<int>>& mat) {
int n = mat.size();
int m = mat[0].size();
vector<vector<int> > left(n,vector<int>(m));
int now = 0;
for(int i=0;i<n;i++){
now = 0;
for(int j=0;j<m;j++){
if(mat[i][j] == 1) now ++;
else now = 0;
left[i][j] = now;
}
}
int ans = 0,minx;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
minx = 0x3f3f3f3f;
for(int k=i;k>=0;k--){
minx = min(left[k][j],minx);
ans += minx;
}
}
}
return ans;
}
};
给你一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。
示例 1：
输入：matrix = [ [0,1,1,1], [1,1,1,1], [0,1,1,1] ] 输出：15 解释： 边长为 1 的正方形有 10 个。 边长为 2 的正方形有 4 个。 边长为 3 的正方形有 1 个。 正方形的总数 = 10 + 4 + 1 = 15.
示例 2：
输入：matrix = [ [1,0,1], [1,1,0], [1,1,0] ] 输出：7 解释： 边长为 1 的正方形有 6 个。 边长为 2 的正方形有 1 个。 正方形的总数 = 6 + 1 = 7.
提示：
1 <= arr.length <= 3001 <= arr[0].length <= 3000 <= arr[i][j] <= 1思路启发：学习 二维前缀和 对于想出本题的转移方程有帮助。
整理上图中的结论。定义 $f_{i,j}$ 为右下角在 $(i,j)$ 的全 $1$ 正方形的最大边长。我们有
$$
f_{i,j} =
\begin{cases}
0, & \textit{matrix}{i,j} = 0 \
\min(f{i-1,j-1},f_{i-1,j},f_{i,j-1}) + 1, & \textit{matrix}_{i,j} = 1 \
\end{cases}
$$
然而，当 $i=0$ 或者 $j=0$ 时，上式会产生负数下标 $-1$。
为避免出现负数下标，可以在 $f$ 矩阵的最上边添加一行 $0$，最左边添加一列 $0$，对应下标出界的状态（正方形的最大边长为 $0$）。
由于修改了 $f$，状态转移方程中的 $f$ 的下标要加一，即
$$
f_{i+1,j+1} =
\begin{cases}
0, & \textit{matrix}{i,j} = 0 \
\min(f{i,j},f_{i,j+1},f_{i+1,j}) + 1, & \textit{matrix}_{i,j} = 1 \
\end{cases}
$$
注意 $\textit{matrix}$ 的下标是不用变的，因为我们只是在 $f$ 矩阵的上边和左边插入了 $0$，所以只有 $f$ 的下标受此影响需要加一。
初始值 $f_{0,j} = f_{i,0} = 0$。
根据图中的结论（个数等于最大边长），答案为整个 $f$ 矩阵的元素和。
###py
class Solution:
def countSquares(self, matrix: List[List[int]]) -> int:
m, n = len(matrix), len(matrix[0])
f = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(matrix):
for j, x in enumerate(row):
if x:
f[i + 1][j + 1] = min(f[i][j], f[i][j + 1], f[i + 1][j]) + 1
return sum(map(sum, f))
###java
class Solution {
public int countSquares(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[][] f = new int[m + 1][n + 1];
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] > 0) {
f[i + 1][j + 1] = Math.min(Math.min(f[i][j], f[i][j + 1]), f[i + 1][j]) + 1;
ans += f[i + 1][j + 1];
}
}
}
return ans;
}
}
###cpp
class Solution {
public:
int countSquares(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector f(m + 1, vector<int>(n + 1));
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j]) {
f[i + 1][j + 1] = min({f[i][j], f[i][j + 1], f[i + 1][j]}) + 1;
ans += f[i + 1][j + 1];
}
}
}
return ans;
}
};
###go
func countSquares(matrix [][]int) (ans int) {
m, n := len(matrix), len(matrix[0])
f := make([][]int, m+1)
for i := range f {
f[i] = make([]int, n+1)
}
for i, row := range matrix {
for j, x := range row {
if x > 0 {
f[i+1][j+1] = min(f[i][j], f[i][j+1], f[i+1][j]) + 1
ans += f[i+1][j+1]
}
}
}
return
}
直接把 $\textit{matrix}$ 当作 $f$，原地修改。
###py
class Solution:
def countSquares(self, matrix: List[List[int]]) -> int:
for i, row in enumerate(matrix):
for j, x in enumerate(row):
if x and i and j:
row[j] += min(matrix[i - 1][j], matrix[i - 1][j - 1], row[j - 1])
return sum(map(sum, matrix))
###java
class Solution {
public int countSquares(int[][] matrix) {
int ans = 0;
for (int i = 0; i < matrix.length; i++) {
int[] row = matrix[i];
for (int j = 0; j < row.length; j++) {
if (row[j] > 0 && i > 0 && j > 0) {
row[j] += Math.min(Math.min(matrix[i - 1][j], matrix[i - 1][j - 1]), row[j - 1]);
}
ans += row[j];
}
}
return ans;
}
}
###cpp
class Solution {
public:
int countSquares(vector<vector<int>>& matrix) {
int ans = 0;
for (int i = 0; i < matrix.size(); i++) {
auto& row = matrix[i];
for (int j = 0; j < row.size(); j++) {
if (i && j && row[j]) {
row[j] += min({matrix[i - 1][j], matrix[i - 1][j - 1], row[j - 1]});
}
ans += row[j];
}
}
return ans;
}
};
###go
func countSquares(matrix [][]int) (ans int) {
for i, row := range matrix {
for j, x := range row {
if x > 0 && i > 0 && j > 0 {
row[j] += min(matrix[i-1][j], matrix[i-1][j-1], row[j-1])
}
ans += row[j]
}
}
return
}
见下面动态规划题单的「§7.5 子矩形 DP」。
欢迎关注 B站@灵茶山艾府
思路
我们用 $f[i][j]$ 表示以 $(i, j)$ 为右下角的正方形的最大边长，那么除此定义之外，$f[i][j] = x$ 也表示以 $(i, j)$ 为右下角的正方形的数目为 $x$（即边长为 $1, 2, \cdots, x$ 的正方形各一个）。在计算出所有的 $f[i][j]$ 后，我们将它们进行累加，就可以得到矩阵中正方形的数目。
我们尝试挖掘 $f[i][j]$ 与相邻位置的关系来计算出 $f[i][j]$ 的值。
如上图所示，若对于位置 $(i, j)$ 有 $f[i][j] = 4$，我们将以 $(i, j)$ 为右下角、边长为 $4$ 的正方形涂上色，可以发现其左侧位置 $(i, j - 1)$，上方位置 $(i - 1, j)$ 和左上位置 $(i - 1, j - 1)$ 均可以作为一个边长为 $4 - 1 = 3$ 的正方形的右下角。也就是说，这些位置的的 $f$ 值至少为 $3$，即：
将这三个不等式联立，可以得到：
$$\texttt{min}(f[i][j−1],f[i−1][j],f[i−1][j−1])\ge f[i][j]−1$$
这是我们通过固定 $f[i][j]$ 的值，判断其相邻位置与之的关系得到的不等式。同理，我们也可以固定 $f[i][j]$ 相邻位置的值，得到另外的限制条件。
如上图所示，假设 $f[i][j - 1]$，$f[i - 1][j]$ 和 $f[i - 1][j - 1]$ 中的最小值为 $3$，即，$(i, j - 1)$，$(i - 1, j)$ 和 $(i - 1, j - 1)$ 均可以作为一个边长为 $3$ 的正方形的右下角。我们将这些边长为 $3$ 的正方形依次涂上色，可以发现，如果位置 $(i, j)$ 的元素为 $1$，那么它可以作为一个边长为 $4$ 的正方形的右下角，$f$ 值至少为 $4$，即：
$$f[i][j]\geq \texttt{min}(f[i][j−1],f[i−1][j],f[i−1][j−1])+1$$
将其与上一个不等式联立，可以得到：
$$f[i][j] = \texttt{min}(f[i][j−1],f[i−1][j],f[i−1][j−1])+1$$
再考虑一些边界情况，我们就得到了完整的递推式：
$$
f[i][j] =
\begin{cases}
matrix[i][j] & \texttt{if } i=0 \texttt{ or } j=0 \
0 & \texttt{if } matrix[i][j]=0 \
\min(f[i][j-1], f[i-1][j], f[i-1][j-1]) + 1 & \texttt{otherwise}
\end{cases}
$$
我们按照行优先的顺序依次计算 $f[i][j]$ 的值，累加就可以得到最终的答案。
代码
###Python
class Solution:
def countSquares(self, matrix: List[List[int]]) -> int:
m, n = len(matrix), len(matrix[0])
f = [[0] * n for _ in range(m)]
ans = 0
for i in range(m):
for j in range(n):
if i == 0 or j == 0:
f[i][j] = matrix[i][j]
elif matrix[i][j] == 0:
f[i][j] = 0
else:
f[i][j] = min(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]) + 1
ans += f[i][j]
return ans
###C++
class Solution {
public:
int countSquares(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> f(m, vector<int>(n, 0));
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || j == 0) {
f[i][j] = matrix[i][j];
} else if (matrix[i][j] == 0) {
f[i][j] = 0;
} else {
f[i][j] = min({f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]}) + 1;
}
ans += f[i][j];
}
}
return ans;
}
};
###Java
class Solution {
public int countSquares(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int[][] f = new int[m][n];
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || j == 0) {
f[i][j] = matrix[i][j];
} else if (matrix[i][j] == 0) {
f[i][j] = 0;
} else {
f[i][j] = Math.min(Math.min(f[i][j - 1], f[i - 1][j]), f[i - 1][j - 1]) + 1;
}
ans += f[i][j];
}
}
return ans;
}
}
###C#
public class Solution {
public int CountSquares(int[][] matrix) {
int m = matrix.Length, n = matrix[0].Length;
int[,] f = new int[m, n];
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || j == 0) {
f[i, j] = matrix[i][j];
} else if (matrix[i][j] == 0) {
f[i, j] = 0;
} else {
f[i, j] = Math.Min(Math.Min(f[i, j - 1], f[i - 1, j]), f[i - 1, j - 1]) + 1;
}
ans += f[i, j];
}
}
return ans;
}
}
###Go
func countSquares(matrix [][]int) int {
m, n := len(matrix), len(matrix[0])
f := make([][]int, m)
for i := range f {
f[i] = make([]int, n)
}
ans := 0
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if i == 0 || j == 0 {
f[i][j] = matrix[i][j]
} else if matrix[i][j] == 0 {
f[i][j] = 0
} else {
f[i][j] = min(min(f[i][j - 1], f[i - 1][j]), f[i - 1][j - 1]) + 1
}
ans += f[i][j]
}
}
return ans
}
###C
int countSquares(int** matrix, int matrixSize, int* matrixColSize) {
int m = matrixSize, n = matrixColSize[0];
int** f = (int**)malloc(m * sizeof(int*));
for (int i = 0; i < m; ++i) {
f[i] = (int*)malloc(n * sizeof(int));
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || j == 0) {
f[i][j] = matrix[i][j];
} else if (matrix[i][j] == 0) {
f[i][j] = 0;
} else {
f[i][j] = fmin(f[i][j - 1], fmin(f[i - 1][j], f[i - 1][j - 1])) + 1;
}
ans += f[i][j];
}
}
for (int i = 0; i < m; ++i) {
free(f[i]);
}
free(f);
return ans;
}
###JavaScript
var countSquares = function(matrix) {
const m = matrix.length, n = matrix[0].length;
const f = new Array(m).fill(0).map(() => new Array(n).fill(0));
let ans = 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (i === 0 || j === 0) {
f[i][j] = matrix[i][j];
} else if (matrix[i][j] === 0) {
f[i][j] = 0;
} else {
f[i][j] = Math.min(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]) + 1;
}
ans += f[i][j];
}
}
return ans;
};
###TypeScript
function countSquares(matrix: number[][]): number {
const m = matrix.length, n = matrix[0].length;
const f: number[][] = new Array(m).fill(0).map(() => new Array(n).fill(0));
let ans = 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (i === 0 || j === 0) {
f[i][j] = matrix[i][j];
} else if (matrix[i][j] === 0) {
f[i][j] = 0;
} else {
f[i][j] = Math.min(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]) + 1;
}
ans += f[i][j];
}
}
return ans;
}
###Rust
impl Solution {
pub fn count_squares(matrix: Vec<Vec<i32>>) -> i32 {
let m = matrix.len();
let n = matrix[0].len();
let mut f = vec![vec![0; n]; m];
let mut ans = 0;
for i in 0..m {
for j in 0..n {
if i == 0 || j == 0 {
f[i][j] = matrix[i][j];
} else if matrix[i][j] == 0 {
f[i][j] = 0;
} else {
f[i][j] = f[i][j - 1].min(f[i - 1][j]).min(f[i - 1][j - 1]) + 1;
}
ans += f[i][j];
}
}
ans
}
}
复杂度分析
时间复杂度：$O(m\times n)$，其中 $m$ 和 $n$ 是输入 $\textit{matrix}$ 的行和列。
空间复杂度：$O(m\times n)$。
给你一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。
示例 1：
输入：
matrix =
[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]
输出： 15
解释：
边长为1的正方形有10个。
边长为2的正方形有4个。
边长为3的正方形有1个。
正方形的总数 =10+4+1=15.
示例 2：
输入：
matrix =
[
[1,0,1],
[1,1,0],
[1,1,0]
]
输出： 7
解释：
边长为1的正方形有6个。
边长为2的正方形有1个。
正方形的总数 =6+1=7.
首先，暴力解就是以矩阵每一个点为起点，依次判断边长为1，2，3，...，min{m, n}的区域是否是全1正方形(该区域所有点的和等于该区域面积)，显然，这种复杂度是过不了的。
很容易知道，上述过程在判断较大区域是否为正方形的时候，并没有用到前面计算的结果，每一次判断都从头开始。这也是复杂度过高的原因。
那么怎么利用之前判断过的结果呢？举个例子，比如我要判断以(2, 3)为右下角边长为3的正方形区域（红色边框区域）是否是全为1：
(i, j)位置是否为1，如果否，则显然不满足；如果是，进行下一步判断(i - 1, j), (i - 1, j - 1), (i, j - 1)为右下角的区域是否能构成边长为2的正方形，如果能，那就满足条件。
基于上述，我们可以看出思路大致跟最大正方形那题差不多，设dp[i][j][k]表示以(i, j)为右下角，边长为k的正方形区域是否全为1，那么易得出如下状态转移方程：
###java
dp[i][j][k] = (matrix[i][j] == 1 && dp[i - 1][j][k - 1] && dp[i][j - 1][k - 1] && dp[i - 1][j - 1] [k - 1]);
###java
class Solution {
public int countSquares(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int len = Math.min(m, n);
boolean[][][] dp = new boolean[m][n][len];
int count = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
dp[i][j][0] = (matrix[i][j] == 1);
count += dp[i][j][0] ? 1 : 0;
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
for (int k = 1; k < len; k++) {
dp[i][j][k] = (matrix[i][j] == 1 && dp[i - 1][j][k - 1] && dp[i][j - 1][k - 1] && dp[i - 1][j - 1] [k - 1]);
if (dp[i][j][k]) {
count++;
}
}
}
}
return count;
}
}
经评论区@da-fei-kai提醒，上述代码可以做进一步优化。
首先，题目并不关心边长为
1,2,...,k的各有多少个，并且我们知道，以(i, j)为右下角边长为k的正方形全为1的话，那么以(i, j)为右下角边长分别为1,2,...,k - 1的正方形区域一定是全为1，如下图：
上图中，如果红色区域是边长为
3的全1正方形区域，那么它一定包含了一个边长为2和边长为1的全1正方形区域。所以，我们只需记录以(i, j)为右下角的区域包含的最大全1正方形边长即可，这个最大边长也即以(i , j)为右下角的全1正方形的个数.
那么基于此，我们就可以将原始的dp降一维度，设dp[i][j]表示以(i, j)为右下角的最大全1正方形区域的边长，则有如下状态转移方程：
###java
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
这就和最大正方形那题的状态转移方程完全一样了。
###java
class Solution {
public int countSquares(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[][] dp = new int[m][n];
int ans = 0;
// 预处理每一行和每一列
for (int i = 0; i < m; i++) {
ans += dp[i][0] = matrix[i][0];
}
for (int j = 0; j < n; j++) {
ans += dp[0][j] = matrix[0][j];
}
// 上述过程(0, 0)判断了两次, 如果matrix[0][0] == 1，说明ans多算了一个
if (matrix[0][0] == 1) {
ans--;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == 1) {
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
ans += dp[i][j];
}
}
}
return ans;
}
}
给你一个整数数组 nums ，返回全部为 0 的 子数组 数目。
子数组 是一个数组中一段连续非空元素组成的序列。
示例 1：
输入：nums = [1,3,0,0,2,0,0,4] 输出：6 解释： 子数组 [0] 出现了 4 次。 子数组 [0,0] 出现了 2 次。 不存在长度大于 2 的全 0 子数组，所以我们返回 6 。
示例 2：
输入：nums = [0,0,0,2,0,0] 输出：9 解释： 子数组 [0] 出现了 5 次。 子数组 [0,0] 出现了 3 次。 子数组 [0,0,0] 出现了 1 次。 不存在长度大于 3 的全 0 子数组，所以我们返回 9 。
示例 3：
输入：nums = [2,10,2019] 输出：0 解释：没有全 0 子数组，所以我们返回 0 。
提示：
1 <= nums.length <= 105-109 <= nums[i] <= 109本题做法很多，下面讲两个更具一般性的方法。
子数组越长，越可能包含非零元素，不满足题目要求；子数组越短，越可能全为 $0$，满足题目要求。我们枚举子数组的右端点，当右端点变大（子数组变长）的时候，子数组左端点要么不变，要么也变大。
不仅是本题，有这样性质的题目，都可以用滑动窗口解决，见 滑动窗口【基础算法精讲 03】。
本题属于「越短越合法」型滑动窗口。由于题目的特殊性，有更简单的解决方法：
示例 1 的 $\textit{nums} = [1,3,0,0,2,0,0,4]$，当右端点在 $i=3$ 时，$\textit{last}=1$，我们找到了 $i-\textit{last}=2$ 个右端点在 $3$ 的全 $0$ 子数组，加入答案。
为了兼容 $\textit{nums}=[0,0,0,2,0,0]$ 这种一开始就是 $0$ 的情况，初始化 $\textit{last}=-1$。
class Solution:
def zeroFilledSubarray(self, nums: List[int]) -> int:
ans = 0
last = -1
for i, x in enumerate(nums):
if x:
last = i # 记录上一个非 0 元素的位置
else:
ans += i - last
return ans
class Solution {
public long zeroFilledSubarray(int[] nums) {
long ans = 0;
int last = -1;
for (int i = 0; i < nums.length; i++) {
int x = nums[i];
if (x != 0) {
last = i; // 记录上一个非 0 元素的位置
} else {
ans += i - last;
}
}
return ans;
}
}
class Solution {
public:
long long zeroFilledSubarray(vector<int>& nums) {
long long ans = 0;
int last = -1;
for (int i = 0; i < nums.size(); i++) {
if (nums[i]) {
last = i; // 记录上一个非 0 元素的位置
} else {
ans += i - last;
}
}
return ans;
}
};
long long zeroFilledSubarray(int* nums, int numsSize) {
long long ans = 0;
int last = -1;
for (int i = 0; i < numsSize; i++) {
if (nums[i]) {
last = i; // 记录上一个非 0 元素的位置
} else {
ans += i - last;
}
}
return ans;
}
func zeroFilledSubarray(nums []int) (ans int64) {
last := -1
for i, x := range nums {
if x != 0 {
last = i // 记录上一个非 0 元素的位置
} else {
ans += int64(i - last)
}
}
return
}
var zeroFilledSubarray = function(nums) {
let ans = 0;
let last = -1;
for (let i = 0; i < nums.length; i++) {
if (nums[i] !== 0) {
last = i; // 记录上一个非 0 元素的位置
} else {
ans += i - last;
}
}
return ans;
};
impl Solution {
pub fn zero_filled_subarray(nums: Vec<i32>) -> i64 {
let mut ans = 0;
let mut last = -1;
for (i, x) in nums.into_iter().enumerate() {
let i = i as i64;
if x != 0 {
last = i; // 记录上一个非 0 元素的位置
} else {
ans += (i - last) as i64;
}
}
ans
}
}
遍历到 $\textit{nums}[i]=0$，现在来计算右端点为 $i$ 的全 $0$ 子数组的个数。
我们可以在右端点为 $i-1$ 的全 $0$ 子数组的末尾添加一个 $0$。比如右端点为 $i-1$ 的全 $0$ 子数组有 $5$ 个，那么在这 $5$ 个子数组的末尾添加 $\textit{nums}[i]=0$，再算上 $\textit{nums}[i]$ 单独组成一个长为 $1$ 的子数组，我们得到了 $5+1=6$ 个右端点为 $i$ 的全 $0$ 子数组，加入答案。
具体来说：
class Solution:
def zeroFilledSubarray(self, nums: List[int]) -> int:
ans = cnt0 = 0
for x in nums:
if x:
cnt0 = 0
else:
cnt0 += 1 # 右端点为 i 的全 0 子数组比右端点为 i-1 的全 0 子数组多一个
ans += cnt0
return ans
class Solution {
public long zeroFilledSubarray(int[] nums) {
long ans = 0;
int cnt0 = 0;
for (int x : nums) {
if (x != 0) {
cnt0 = 0;
} else {
cnt0++; // 右端点为 i 的全 0 子数组比右端点为 i-1 的全 0 子数组多一个
ans += cnt0;
}
}
return ans;
}
}
class Solution {
public:
long long zeroFilledSubarray(vector<int>& nums) {
long long ans = 0;
int cnt0 = 0;
for (int x : nums) {
if (x) {
cnt0 = 0;
} else {
cnt0++; // 右端点为 i 的全 0 子数组比右端点为 i-1 的全 0 子数组多一个
ans += cnt0;
}
}
return ans;
}
};
long long zeroFilledSubarray(int* nums, int numsSize) {
long long ans = 0;
int cnt0 = 0;
for (int i = 0; i < numsSize; i++) {
if (nums[i]) {
cnt0 = 0;
} else {
cnt0++; // 右端点为 i 的全 0 子数组比右端点为 i-1 的全 0 子数组多一个
ans += cnt0;
}
}
return ans;
}
func zeroFilledSubarray(nums []int) (ans int64) {
cnt0 := 0
for _, x := range nums {
if x != 0 {
cnt0 = 0
} else {
cnt0++ // 右端点为 i 的全 0 子数组比右端点为 i-1 的全 0 子数组多一个
ans += int64(cnt0)
}
}
return
}
var zeroFilledSubarray = function(nums) {
let ans = 0;
let cnt0 = 0;
for (const x of nums) {
if (x !== 0) {
cnt0 = 0;
} else {
cnt0++; // 右端点为 i 的全 0 子数组比右端点为 i-1 的全 0 子数组多一个
ans += cnt0;
}
}
return ans;
};
impl Solution {
pub fn zero_filled_subarray(nums: Vec<i32>) -> i64 {
let mut ans = 0;
let mut cnt0 = 0;
for x in nums {
if x != 0 {
cnt0 = 0;
} else {
cnt0 += 1; // 右端点为 i 的全 0 子数组比右端点为 i-1 的全 0 子数组多一个
ans += cnt0 as i64;
}
}
ans
}
}
注：本题还有其他方法，例如找极大连续 $0$ 的长度，然后用等差数列计算。
方法一：滑动窗口题单的「§2.3.1 越短越合法」。
方法二：动态规划题单「§7.3 子数组 DP」的「思维扩展」。
欢迎关注 B站@灵茶山艾府
###python3
class Solution:
def zeroFilledSubarray(self, nums: List[int]) -> int:
groups = [(char, len(list(group))) for char, group in groupby(nums)]
return sum(count * (count + 1) // 2 for char, count in groups if char == 0)
