滑动窗口优化 DP,简洁写法(Python/Java/C++/C/Go/JS/Rust)
寻找子问题
我们要解决的问题(原问题)是:
- 从 $0$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率。
用「枚举选哪个」思考,即枚举我们获得多少分:
- 有 $\dfrac{1}{\textit{maxPts}}$ 的概率获得 $1$ 分,问题变成从 $1$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率。
- 有 $\dfrac{1}{\textit{maxPts}}$ 的概率获得 $2$ 分,问题变成从 $2$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率。
- 有 $\dfrac{1}{\textit{maxPts}}$ 的概率获得 $3$ 分,问题变成从 $3$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率。
- ……
- 有 $\dfrac{1}{\textit{maxPts}}$ 的概率获得 $\textit{maxPts}$ 分,问题变成从 $\textit{maxPts}$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率。
这些问题都是和原问题相似的、规模更小的子问题。
状态定义与状态转移方程
根据上面的讨论,定义 $f[i]$ 表示从 $i$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率。
在当前回合,我们等概率地发生以下 $\textit{\textit{maxPts}}$ 种事件:
- 获得 $1$ 分。问题变成从 $i+1$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率,即 $f[i+1]$。
- 获得 $2$ 分。问题变成从 $i+2$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率,即 $f[i+2]$。
- 获得 $3$ 分。问题变成从 $i+3$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率,即 $f[i+3]$。
- ……
- 获得 $\textit{maxPts}$ 分。问题变成从 $i+\textit{maxPts}$ 分开始游戏,最终到达闭区间 $[k,n]$ 的概率,即 $f[i+\textit{maxPts}]$。
由于上述 $\textit{\textit{maxPts}}$ 种事件互斥且等概率地被选择,因此最终到达闭区间 $[k,n]$ 的概率为上述 $\textit{\textit{maxPts}}$ 个状态值的平均值,即
$$
f[i] = \dfrac{f[i+1] + f[i+2] + f[i+3] + \dots + f[i+\textit{maxPts}]}{\textit{maxPts}}
$$
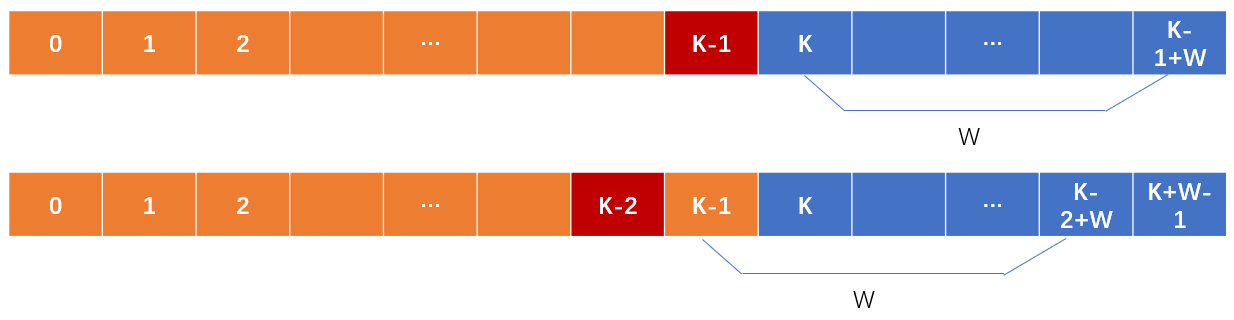
由于转移来源比 $i$ 大,所以要倒序枚举 $i$。
由于转移方程中的分子是一个长度固定为 $\textit{maxPts}$ 的连续子数组的元素和,所以可以用定长滑动窗口 $\mathcal{O}(1)$ 计算,原理讲解请看【套路】教你解决定长滑窗!适用于所有定长滑窗题目!
初始值:
- 当 $k\le i\le n$ 时,游戏结束,由于到达闭区间 $[k,n]$,所以 $f[i]=1$。
- 当 $i > n$ 时,游戏结束,由于在闭区间 $[k,n]$ 外,所以 $f[i]=0$。代码实现时,可以直接创建大小为 $n+1$ 的 $f$ 数组,下标出界就表示 $f[i]=0$。
答案:$f[0]$,即原问题。
答疑
问:为什么滑动窗口的计算顺序不是「入-计算-出」,而是「计算-入-出」?
答:当我们遍历到 $i$ 时,窗口的左端点是 $i+1$ 而不是 $i$。所以 $f[i]$ 并不在窗口中,得先把 $f[i]$ 计算出来,然后下个循环 $f[i]$ 才在窗口中。
注:$n$ 可以与 $k+\textit{maxPts}$ 取 $\min$,但测试发现这个优化不显著。
###py
class Solution:
def new21Game(self, n: int, k: int, maxPts: int) -> float:
f = [0.0] * (n + 1)
s = 0.0
for i in range(n, -1, -1):
f[i] = 1.0 if i >= k else s / maxPts
# 当前循环计算的是 f[i+1] + ... + f[i+maxPts]
# 下个循环计算的是 f[i] + ... + f[i+maxPts-1],多了 f[i],少了 f[i+maxPts]
s += f[i]
if i + maxPts <= n:
s -= f[i + maxPts]
return f[0]
###java
class Solution {
public double new21Game(int n, int k, int maxPts) {
double[] f = new double[n + 1];
double s = 0;
for (int i = n; i >= 0; i--) {
f[i] = i >= k ? 1 : s / maxPts;
// 当前循环计算的是 f[i+1] + ... + f[i+maxPts]
// 下个循环计算的是 f[i] + ... + f[i+maxPts-1],多了 f[i],少了 f[i+maxPts]
s += f[i];
if (i + maxPts <= n) {
s -= f[i + maxPts];
}
}
return f[0];
}
}
###cpp
class Solution {
public:
double new21Game(int n, int k, int maxPts) {
vector<double> f(n + 1);
double s = 0;
for (int i = n; i >= 0; i--) {
f[i] = i >= k ? 1 : s / maxPts;
// 当前循环计算的是 f[i+1] + ... + f[i+maxPts]
// 下个循环计算的是 f[i] + ... + f[i+maxPts-1],多了 f[i],少了 f[i+maxPts]
s += f[i];
if (i + maxPts <= n) {
s -= f[i + maxPts];
}
}
return f[0];
}
};
###c
double new21Game(int n, int k, int maxPts) {
double* f = malloc((n + 1) * sizeof(double));
double s = 0;
for (int i = n; i >= 0; i--) {
f[i] = i >= k ? 1 : s / maxPts;
// 当前循环计算的是 f[i+1] + ... + f[i+maxPts]
// 下个循环计算的是 f[i] + ... + f[i+maxPts-1],多了 f[i],少了 f[i+maxPts]
s += f[i];
if (i + maxPts <= n) {
s -= f[i + maxPts];
}
}
double ans = f[0];
free(f);
return ans;
}
###go
func new21Game(n, k, maxPts int) float64 {
f := make([]float64, n+1)
s := 0.0
for i := n; i >= 0; i-- {
if i >= k {
f[i] = 1 // 初始值
} else {
f[i] = s / float64(maxPts)
}
// 当前循环计算的是 f[i+1] + ... + f[i+maxPts]
// 下个循环计算的是 f[i] + ... + f[i+maxPts-1],多了 f[i],少了 f[i+maxPts]
s += f[i]
if i+maxPts <= n {
s -= f[i+maxPts]
}
}
return f[0]
}
###js
var new21Game = function(n, k, maxPts) {
const f = new Array(n + 1).fill(0);
let s = 0;
for (let i = n; i >= 0; i--) {
f[i] = i >= k ? 1 : s / maxPts;
// 当前循环计算的是 f[i+1] + ... + f[i+maxPts]
// 下个循环计算的是 f[i] + ... + f[i+maxPts-1],多了 f[i],少了 f[i+maxPts]
s += f[i];
if (i + maxPts <= n) {
s -= f[i + maxPts];
}
}
return f[0];
};
###rust
impl Solution {
pub fn new21_game(n: i32, k: i32, max_pts: i32) -> f64 {
let n = n as usize;
let k = k as usize;
let max_pts = max_pts as usize;
let mut f = vec![0.0; n + 1];
let mut s = 0.0;
for i in (0..=n).rev() {
f[i] = if i >= k { 1.0 } else { s / max_pts as f64 };
// 当前循环计算的是 f[i+1] + ... + f[i+maxPts]
// 下个循环计算的是 f[i] + ... + f[i+maxPts-1],多了 f[i],少了 f[i+maxPts]
s += f[i];
if i + max_pts <= n {
s -= f[i + max_pts];
}
}
f[0]
}
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n)$。
- 空间复杂度:$\mathcal{O}(n)$。
专题训练
见下面动态规划题单的「十五、概率/期望 DP」和「§11.1 前缀和优化 DP」。
分类题单
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 二分算法(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流)
- 动态规划(入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、二叉树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA/一般树)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)