❌

阅读视图

发现新文章，点击刷新页面。

每日一题-新 21 点🟡

✇LeetCode 每日一题题解

爱丽丝参与一个大致基于纸牌游戏 “21点” 规则的游戏，描述如下：

爱丽丝以 0 分开始，并在她的得分少于 k 分时抽取数字。 抽取时，她从 [1, maxPts] 的范围中随机获得一个整数作为分数进行累计，其中 maxPts 是一个整数。 每次抽取都是独立的，其结果具有相同的概率。

当爱丽丝获得 k 分 或更多分 时，她就停止抽取数字。

爱丽丝的分数不超过 n 的概率是多少？

与实际答案误差不超过 10-5 的答案将被视为正确答案。

 

示例 1：

输入：n = 10, k = 1, maxPts = 10
输出：1.00000
解释：爱丽丝得到一张牌，然后停止。

示例 2：

输入：n = 6, k = 1, maxPts = 10
输出：0.60000
解释：爱丽丝得到一张牌，然后停止。 在 10 种可能性中的 6 种情况下，她的得分不超过 6 分。

示例 3：

输入：n = 21, k = 17, maxPts = 10
输出：0.73278

 

提示：

  • 0 <= k <= n <= 104
  • 1 <= maxPts <= 104

还有比这更简单的题解吗？填格子游戏开始

✇LeetCode 每日一题题解
Mcdull0921

解题思路

老实说，一开始没懂题目意思，后面才知道是求爱丽丝的胜率。
规则是这样：

  1. 她可以从牌面为 [1,W] 的牌中选择任意一张，这张牌是可以无限重复的，也就是说无论她取多少次，每次取到 2（假如 2 在 [1,W] 范围内）的概率都是 1/W;
  2. 如果她手上牌的总额小于 K，她就会抽牌，大于等于 K 时，就停止抽牌;
  3. 停止抽牌后，她的牌面小于等于 N 时，她就获胜了，求她获胜的概率。

假设 dp[x] 为她手上牌面为x时，能获胜的概率，那么这个概率应该是：
dp[x]=1/w * (dp[x+1]+dp[x+2]+dp[x+3]...+dp[x+w])
因为抽取的牌面机会都是均等的，她能抽取的面值在 [1,W] 之间，所以将概率之和平均一下就是 dp[x] 的概率。

强插一段解释：
x代表爱丽丝手上的牌面值，dp[x]代表爱丽丝手上持有的牌面值为x时，她获胜的概率（游戏结束时她所持牌面值小于等于N的概率）。
这个概率是怎么来的？x分2种情况:

  1. 当x>=K时，爱丽丝会停止抽牌，这个时候游戏已经结束了，她是赢是输也已经确定了，所以此时赢的概率要么1，要么0
  2. 当x<K时，爱丽丝会继续抽牌，抽牌是有概率的，所以她是赢是输也有概率。
    她能抽到的牌面值在 [1,W] 之间，所以抽完后她的牌面在[x+1,x+w]之间，因为每张牌机率均等，所以抽完后牌面在[x+1,x+w]之间的每个面值概率都是相等的，而假如我们已知当牌面是[x+1,x+w]的胜率(即dp[x+1]...dp[x+w]的值)，那么可以推导：
    dp[x]=1/w * dp[x+1]+ 1/w * dp[x+2] + 1/w * dp[x+3]...+ 1/w * dp[x+w]
    这个实际上就是动态规划的状态转移方程，不过本例是反着来转移的。

x 最多能到 K-1，因为当大于等于 K 时，爱丽丝会停止抽牌，所以当游戏结束时，即爱丽丝停止抽牌时，她可能达到的最大牌面是 K+W-1，而一开始她的牌面是 0，所以我们用一个长度为 K+W 的 dp 数组来保存她在所有面值下的胜率。
最后 dp[0]，也就是最开始爱丽丝还没有抽牌，她的牌面为 0 时的胜率，这个就是我们的答案。

填格子游戏开始

image.png

我将这个格子分成了 2 部分 [0,K-1] 和 [K,K+W-1]，区别就是 [0,K-1] 爱丽丝可以抽牌，[K,K+W-1] 时不能抽牌，那么不能抽牌时她获胜的概率是多少呢，此时已不能抽牌，要么赢要么输，很显然牌面小于等于N时，概率就是 1，大于 N 概率就是 0，所以先直接填满图中蓝色的格子。

接下来，从 K-1 开始填图中的橘色部分，这个值根据我们前面提到的计算方式，实际上就相当于它后面 W 个格子的总和除以 W，
这时聪明的你一定会想到不用每轮都累加的方法吧，用一个 s 变量来保存累加结果，而下一轮只是减去右边的格子，加上左边的格子即可。

image.png

所以这题你要做的就是，先初始化蓝色格子，然后从最右边的橘色格子开始，填到最左边的格子，就是这么简单，不仅简单，而且你连动态规划的思想都学会了。
相信这么厉害的你，看到这里给我点个赞一定不是件很困难的事吧。

代码

###Python3

class Solution:
    def new21Game(self, N: int, K: int, W: int) -> float:
        dp=[None]*(K+W)
        s=0
        for i in range(K,K+W):          # 填蓝色的格子
            dp[i] = 1 if i<=N else 0
            s+=dp[i]
        for i in range(K-1,-1,-1):      # 填橘黄色格子
            dp[i]=s/W
            s=s-dp[i+W]+dp[i]
        return dp[0]

时间复杂度=格子长度 $O(K+W)$
空间复杂度=格子长度 $O(K+W)$

怎样得到官方题解中的状态转移方程

✇LeetCode 每日一题题解
sour-e

怎样推导出官方题解中的状态转移方程

按照官方题解的说明，$dp[x]$ 表示从得分为$x$的情况开始游戏并且获胜的概率，如果我们引入 $x_t=x$ 表示$t$ 时刻的总分是 $x$，那么 $dp[x]$ 用条件概率可以写作
$$
dp[x] = P(win | x_t = x)
$$
我们怎么利用这个条件概率来得到题解中的状态转移方程呢？从条件概率可以联想到全概率公式。拿总分 $x=K - 1$ 为例，
$$
dp[K - 1] = P(win | x_t = K - 1) \
= \sum_{i=1}^{W} P(win | x_{t+1} = K - 1 + i) P(x_{t + 1} = K - 1 + i | x_t = K - 1)
$$
其中，$P(x_{t + 1} = K - 1 + i | x_t = K - 1)$ 表示，在 $t$ 时刻，一次抽取后，总分从 $K - 1$ 变成 $K - 1 + i$ 的概率，这实际上就是当前抽到数字 $i$ 的概率，根据题目

抽取时，她从 [1, W] 的范围中随机获得一个整数作为分数进行累计，其中 W 是整数。每次抽取都是独立的，其结果具有相同的概率

我们知道在任意时刻抽取得到 ${1, 2, .., W}$ 的概率相同（抽取的数字服从离散型均匀分布），即
$$
P(x_{t + 1} = K - 1 + i | x_t = K - 1) = P(\Delta x_t = i) = \frac{1}{W}
$$
另外，$P(win | x_{t+1} = K - 1 + i) = dp[K - 1 + i]$，我们就得到了官方题解里的状态转移方程
$$
dp[K - 1] = P(win | x_t = K - 1) \
= \sum_{i=1}^{W} P(x_{t + 1} = K - 1 + i | x_t = K - 1) P(win | x_{t+1} = K - 1 + i) \
= \sum_{i=1}^{W} \frac{1}{W} \cdot dp[K - 1 + i]\
= \frac{dp[K] + dp[K + 1] + ... + dp[K - 1 + W]}{W}
$$

延申

  1. 我们定义的$t$时刻总分$x_t$其实是一个马尔科夫链

    • 它有马尔可夫性$P(x_{t+1}| x_{t}, x_{t - 1}, ..., x_{1}) = P(x_{t+1} | x_{t})$，即下一状态（抽一次后的总分）的分布只与当前状态（当前总分）有关，而与之前的状态（之前的总分）无关。
    • 在题目中我们仅关心抽取一次后的总分概率$P(x_{t+1} = j| x_{t} = i)$，这个概率与当前时间$t$无关，这样的马尔科夫链叫齐次马尔科夫链。
    • 我们进而可以把上述概率写作$P(x_{t+1} = j| x_{t} = i) = p_{i,j}$，$p_{i,j}$也被称作一步转移概率，相应地也有$n$步转移概率$P(x_{t+n} = j| x_{t} = i) = p_{i,j}^{(n)}$，即抽取n次后总分$x_{t+n}$的分布，$n$步转移概率需要用C-K方程求解。

  2. 题目中，抽取时，她从 [1, W] 的范围中随机获得一个整数作为分数进行累计，其中 W 是整数。每次抽取都是独立的，其结果具有相同的概率的条件对玩家每一次抽取到数字的分布做出了假设，即假设 “无论玩家当前总分是多少，玩家抽到任意数字的概率都相等”，用转移概率表示就是 $P(x_{t + 1} = x + i | x_t = x) = \frac{1}{W}$，其中 $i \in {1,2,..,W}$，考虑以下两种情况

    • 假设玩家当前收到数字的概率与其当前总分有关，即 $P(x_{t + 1} = x + i | x_t = x) = f(x, W)$，比如在一些赌场，玩家当前总分越高，发牌器中混入更多大牌，给玩家发到小牌的概率越小，玩家更容易爆掉。
    • 假设玩家当前收到数字的概率不仅与其当前总分有关，还和玩家游玩时间有关，即 $P(x_{t + 1} = x + i | x_t = x) = f(x, W, t)$，比如在一些赌场，玩家游玩时间越久，发牌器中混入的大牌越多，给玩家发到小牌的概率越小，让玩家更容易爆掉。

    第一种情况和原题类似，同属于齐次马尔可夫链（即转移概率不随时间变化而变化），第二种情况属于非齐次马尔科夫链，求解更加复杂。

  3. 如果我们把上面 抽取时，她从 [1, W] 的范围中随机获得一个整数作为分数进行累计，其中 W 是整数。每次抽取都是独立的，其结果具有相同的概率 的条件改为 抽取时，她从 [0, 1] 两个数字中抽取W次，以W次抽取结果的和作为分数进行累计，其中 W 是整数，那么每一次增加的分数将服从$n=M$, $p=0.5$的二项分布，状态转移方程也将随之改变为
    $$
    dp[K - 1]
    = \sum_{i=0}^{W} C^{i}_{W} (\frac{1}{2})^{W-i} (\frac{1}{2})^{i} \cdot dp[K - 1 + i]\
    = \frac{dp[K - 1] + W \cdot dp[K] + \frac{W(W-1)}{2} \cdot dp[K + 1] + ... + dp[K - 1 + W]}{2^W}
    $$

新21点

✇LeetCode 每日一题题解
LeetCode-Solution

📺视频题解

837. 新21点 4.mp4

📖文字题解

方法一：动态规划

爱丽丝获胜的概率只和下一轮开始前的得分有关，因此根据得分计算概率。

令 $\textit{dp}[x]$ 表示从得分为 $x$ 的情况开始游戏并且获胜的概率，目标是求 $\textit{dp}[0]$ 的值。

根据规则，当分数达到或超过 $k$ 时游戏结束，游戏结束时，如果分数不超过 $n$ 则获胜，如果分数超过 $n$ 则失败。因此当 $k \le x \le \min(n, k+\textit{maxPts}-1)$ 时有 $\textit{dp}[x]=1$，当 $x>\min(n, k+\textit{maxPts}-1)$ 时有 $\textit{dp}[x]=0$。

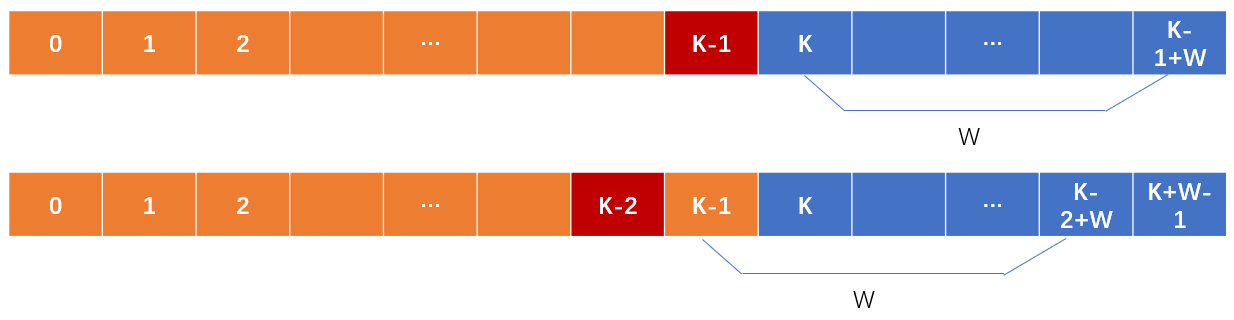
为什么分界线是 $\min(n, k+\textit{maxPts}-1)$？首先，只有在分数不超过 $n$ 时才算获胜；其次，可以达到的最大分数为 $k+\textit{maxPts}-1$，即在最后一次抽取数字之前的分数为 $k-1$，并且抽到了 $\textit{maxPts}$。

当 $0 \le x < k$ 时，如何计算 $\textit{dp}[x]$ 的值？注意到每次在范围 $[1, \textit{maxPts}]$ 内随机抽取一个整数，且每个整数被抽取到的概率相等，因此可以得到如下状态转移方程：

$$
\textit{dp}[x]=\frac{\sum_{i=1}^\textit{maxPts} \textit{dp}[x+i]}{\textit{maxPts}}
$$

根据状态转移方程，可以实现如下简单的动态规划：

###Java

class Solution {
    public double new21Game(int n, int k, int maxPts) {
        if (k == 0) {
            return 1.0;
        }
        double[] dp = new double[k + maxPts];
        for (int i = k; i <= n && i < k + maxPts; i++) {
            dp[i] = 1.0;
        }
        for (int i = k - 1; i >= 0; i--) {
            for (int j = 1; j <= maxPts; j++) {
                dp[i] += dp[i + j] / maxPts;
            }
        }
        return dp[0];
    }
}

###C#

public class Solution {
    public double New21Game(int n, int k, int maxPts) {
        if (k == 0) {
            return 1.0;
        }
        double[] dp = new double[k + maxPts];
        for (int i = k; i <= n && i < k + maxPts; i++) {
            dp[i] = 1.0;
        }
        for (int i = k - 1; i >= 0; i--) {
            for (int j = 1; j <= maxPts; j++) {
                dp[i] += dp[i + j] / maxPts;
            }
        }
        return dp[0];
    }
}

###C++

class Solution {
public:
    double new21Game(int n, int k, int maxPts) {
        if (k == 0) {
            return 1.0;
        }
        vector<double> dp(k + maxPts);
        for (int i = k; i <= n && i < k + maxPts; i++) {
            dp[i] = 1.0;
        }
        for (int i = k - 1; i >= 0; i--) {
            for (int j = 1; j <= maxPts; j++) {
                dp[i] += dp[i + j] / maxPts;
            }
        }
        return dp[0];
    }
};

###Python

class Solution:
    def new21Game(self, n: int, k: int, maxPts: int) -> float:
        if k == 0:
            return 1.0
        dp = [0.0] * (k + maxPts)
        for i in range(k, min(n, k + maxPts - 1) + 1):
            dp[i] = 1.0
        for i in range(k - 1, -1, -1):
            for j in range(1, maxPts + 1):
                dp[i] += dp[i + j] / maxPts
        return dp[0]

###golang

func new21Game(n int, k int, maxPts int) float64 {
    if k == 0 {
        return 1.0
    }
    dp := make([]float64, k + maxPts)
    for i := k; i <= n && i < k + maxPts; i++ {
        dp[i] = 1.0
    }
    for i := k - 1; i >= 0; i-- {
        for j := 1; j <= maxPts; j++ {
            dp[i] += dp[i + j] / float64(maxPts)
        }
    }
    return dp[0]
}

上述解法的时间复杂度是 $O(n+k \times \textit{maxPts})$，会超出时间限制，因此需要优化。

考虑对 $\textit{dp}$ 的相邻项计算差分，有如下结果：

$$
\textit{dp}[x] - \textit{dp}[x+1]=\frac{\textit{dp}[x+1] - \textit{dp}[x+\textit{maxPts}+1]}{\textit{maxPts}}
$$

其中 $0 \le x<k-1$。

因此可以得到新的状态转移方程：

$$
\textit{dp}[x]=\textit{dp}[x+1]-\frac{\textit{dp}[x+\textit{maxPts}+1]-\textit{dp}[x+1]}{\textit{maxPts}}
$$

其中 $0 \le x<k-1$。

注意到上述状态转移方程中 $x$ 的取值范围，当 $x=k-1$ 时不适用。因此对于 $\textit{dp}[k-1]$ 的值，需要通过

$$
\textit{dp}[k-1]=\frac{\sum_{i=0}^{\textit{maxPts}-1} \textit{dp}[k+i]}{\textit{maxPts}}
$$

计算得到。注意到只有当 $k \le x \le \min(n, k+\textit{maxPts}-1)$ 时才有 $\textit{dp}[x]=1$，因此

$$
\textit{dp}[k-1]=\frac{\min(n, k+\textit{maxPts}-1) - k + 1}{\textit{maxPts}} = \frac{\min(n-k+1,\textit{maxPts})}{\textit{maxPts}}
$$

可在 $O(1)$ 时间内计算得到 $\textit{dp}[k-1]$ 的值。

对于 $\textit{dp}[k-2]$ 到 $\textit{dp}[0]$ 的值，则可通过新的状态转移方程得到。

###Java

class Solution {
    public double new21Game(int n, int k, int maxPts) {
        if (k == 0) {
            return 1.0;
        }
        double[] dp = new double[k + maxPts];
        for (int i = k; i <= n && i < k + maxPts; i++) {
            dp[i] = 1.0;
        }
        dp[k - 1] = 1.0 * Math.min(n - k + 1, maxPts) / maxPts;
        for (int i = k - 2; i >= 0; i--) {
            dp[i] = dp[i + 1] - (dp[i + maxPts + 1] - dp[i + 1]) / maxPts;
        }
        return dp[0];
    }
}

###C#

public class Solution {
    public double New21Game(int n, int k, int maxPts) {
        if (k == 0) {
            return 1.0;
        }
        double[] dp = new double[k + maxPts];
        for (int i = k; i <= n && i < k + maxPts; i++) {
            dp[i] = 1.0;
        }
        dp[k - 1] = 1.0 * Math.Min(n - k + 1, maxPts) / maxPts;
        for (int i = k - 2; i >= 0; i--) {
            dp[i] = dp[i + 1] - (dp[i + maxPts + 1] - dp[i + 1]) / maxPts;
        }
        return dp[0];
    }
}

###C++

class Solution {
public:
    double new21Game(int n, int k, int maxPts) {
        if (k == 0) {
            return 1.0;
        }
        vector<double> dp(k + maxPts);
        for (int i = k; i <= n && i < k + maxPts; i++) {
            dp[i] = 1.0;
        }
        dp[k - 1] = 1.0 * min(n - k + 1, maxPts) / maxPts;
        for (int i = k - 2; i >= 0; i--) {
            dp[i] = dp[i + 1] - (dp[i + maxPts + 1] - dp[i + 1]) / maxPts;
        }
        return dp[0];
    }
};

###Python

class Solution:
    def new21Game(self, n: int, k: int, maxPts: int) -> float:
        if k == 0:
            return 1.0
        dp = [0.0] * (k + maxPts)
        for i in range(k, min(n, k + maxPts - 1) + 1):
            dp[i] = 1.0
        dp[k - 1] = float(min(n - k + 1, maxPts)) / maxPts
        for i in range(k - 2, -1, -1):
            dp[i] = dp[i + 1] - (dp[i + maxPts + 1] - dp[i + 1]) / maxPts
        return dp[0]

###golang

func new21Game(n int, k int, maxPts int) float64 {
    if k == 0 {
        return 1.0
    }
    dp := make([]float64, k + maxPts)
    for i := k; i <= n && i < k + maxPts; i++ {
        dp[i] = 1.0
    }

    dp[k - 1] = 1.0 * float64(min(n - k + 1, maxPts)) / float64(maxPts)
    for i := k - 2; i >= 0; i-- {
        dp[i] = dp[i + 1] - (dp[i + maxPts + 1] - dp[i + 1]) / float64(maxPts) 
    }
    return dp[0]
}

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

复杂度分析

  • 时间复杂度：$O(\min(n, k+\textit{maxPts}))$。即需要计算的 $\textit{dp}$ 值的数量 $\min(n, k+\textit{maxPts}-1)$。

  • 空间复杂度：$O(k+\textit{maxPts})$。创建了一个长度为 $k+\textit{maxPts}$ 的数组 $\textit{dp}$。

每日一题-6 和 9 组成的最大数字🟢

✇LeetCode 每日一题题解

给你一个仅由数字 6 和 9 组成的正整数 num。

你最多只能翻转一位数字，将 6 变成 9，或者把 9 变成 6 。

请返回你可以得到的最大数字。

 

示例 1：

输入：num = 9669
输出：9969
解释：
改变第一位数字可以得到 6669 。
改变第二位数字可以得到 9969 。
改变第三位数字可以得到 9699 。
改变第四位数字可以得到 9666 。
其中最大的数字是 9969 。

示例 2：

输入：num = 9996
输出：9999
解释：将最后一位从 6 变到 9，其结果 9999 是最大的数。

示例 3：

输入：num = 9999
输出：9999
解释：无需改变就已经是最大的数字了。

 

提示：

  • 1 <= num <= 10^4
  • num 每一位上的数字都是 6 或者 9 。

两种方法：用字符串/不用字符串（Python/Java/C++/C/Go/JS/Rust）

✇LeetCode 每日一题题解
endlesscheng

分析

要想把数字变大，只能把 $6$ 改成 $9$。

比如 $\textit{num}=9669$：

  • 改高位的 $6$，得到 $9969$。
  • 改低位的 $6$，得到 $9699$。
  • $9969 > 9699$。

改高位的 $6$ 比改低位的 $6$ 更好。由于至多改一次，所以改最高位的 $6$。若 $\textit{num}$ 无 $6$，则 $\textit{num}$ 不变。

方法一：用字符串

###py

class Solution:
    def maximum69Number(self, num: int) -> int:
        s = str(num).replace('6', '9', 1)  # 替换第一个 6
        return int(s)

###py

class Solution:
    def maximum69Number(self, num: int) -> int:
        s = str(num)
        i = s.find('6')
        if i < 0:
            return num
        return int(s[:i] + '9' + s[i + 1:])

###java

class Solution {
    public int maximum69Number(int num) {
        String s = String.valueOf(num).replaceFirst("6", "9"); // 替换第一个 6
        return Integer.parseInt(s);
    }
}

###java

class Solution {
    public int maximum69Number(int num) {
        String s = Integer.toString(num);
        int i = s.indexOf('6');
        if (i < 0) {
            return num;
        }
        s = s.substring(0, i) + "9" + s.substring(i + 1);
        return Integer.parseInt(s);
    }
}

###cpp

class Solution {
public:
    int maximum69Number(int num) {
        string s = to_string(num);
        int i = s.find('6');
        if (i == string::npos) {
            return num;
        }
        s[i] = '9';
        return stoi(s);
    }
};

###c

int maximum69Number(int num) {
    char s[6];
    sprintf(s, "%d", num);
    char* p = strchr(s, '6');
    if (p == NULL) {
        return num;
    }
    *p = '9';
    return atoi(s);
}

###go

func maximum69Number(num int) int {
s := strconv.Itoa(num)
s = strings.Replace(s, "6", "9", 1) // 替换第一个 6
ans, _ := strconv.Atoi(s)
return ans
}

###js

var maximum69Number = function(num) {
    const s = String(num).replace('6', '9'); // 替换第一个 6
    return parseInt(s);
};

###rust

impl Solution {
    pub fn maximum69_number(num: i32) -> i32 {
        num.to_string()
           .replacen("6", "9", 1) // 替换第一个 6
           .parse()
           .unwrap()
    }
}

复杂度分析

  • 时间复杂度：$\mathcal{O}(\log \textit{num})$。
  • 空间复杂度：$\mathcal{O}(\log \textit{num})$。

方法二：不用字符串

可以不用转成字符串处理，而是不断取最低位（模 $10$），去掉最低位（除以 $10$），直到数字为 $0$。

例如 $\textit{num}=9669$：

  1. 初始化 $x=\textit{num}$。
  2. 通过 $x\bmod 10$ 取到个位数 $9$，然后把 $x$ 除以 $10$（下取整），得到 $x=966$。
  3. 再次 $x\bmod 10$ 取到十位数 $6$，然后把 $x$ 除以 $10$（下取整），得到 $x=96$。
  4. 再次 $x\bmod 10$ 取到百位数 $6$，然后把 $x$ 除以 $10$（下取整），得到 $x=9$。
  5. 最后 $x\bmod 10$ 取到千位数 $9$，然后把 $x$ 除以 $10$（下取整），得到 $x=0$。此时完成了遍历 $\textit{num}$ 的每个数位，退出循环。

在这个过程中，维护一个变量 $\textit{base}$，初始值为 $1$，在循环末尾把 $\textit{base}$ 乘以 $10$。每当我们遍历到一个等于 $6$ 的数位，就保存此刻的 $\textit{base}$，即更新 $\textit{maxBase} = \textit{base}$。其中 $\textit{maxBase}$ 初始值为 $0$。由于我们从低位往高位遍历，所以最终的 $\textit{maxBase}$ 就是最高位的 $6$ 对应的 $\textit{base}$。在上面的例子中，我们可以得到 $\textit{maxBase} = 100$。

最终答案为

$$
\textit{num} + \textit{maxBase}\cdot 3
$$

在上面的例子中，答案为 $9669 + 100\cdot 3 = 9969$。

注：如果 $\textit{num}$ 中没有 $6$，由于我们初始化 $\textit{maxBase}=0$，最终答案为 $\textit{num}$。

###py

class Solution:
    def maximum69Number(self, num: int) -> int:
        max_base = 0
        base = 1
        x = num
        while x:
            x, d = divmod(x, 10)
            if d == 6:
                max_base = base
            base *= 10
        return num + max_base * 3

###java

class Solution {
    public int maximum69Number(int num) {
        int maxBase = 0;
        int base = 1;
        for (int x = num; x > 0; x /= 10) {
            if (x % 10 == 6) {
                maxBase = base;
            }
            base *= 10;
        }
        return num + maxBase * 3;
    }
}

###cpp

class Solution {
public:
    int maximum69Number(int num) {
        int max_base = 0;
        int base = 1;
        for (int x = num; x > 0; x /= 10) {
            if (x % 10 == 6) {
                max_base = base;
            }
            base *= 10;
        }
        return num + max_base * 3;
    }
};

###c

int maximum69Number(int num) {
    int max_base = 0;
    int base = 1;
    for (int x = num; x > 0; x /= 10) {
        if (x % 10 == 6) {
            max_base = base;
        }
        base *= 10;
    }
    return num + max_base * 3;
}

###go

func maximum69Number(num int) int {
maxBase := 0
base := 1
for x := num; x > 0; x /= 10 {
if x%10 == 6 {
maxBase = base
}
base *= 10
}
return num + maxBase*3
}

###js

var maximum69Number = function(num) {
    let maxBase = 0;
    let base = 1;
    for (let x = num; x > 0; x = Math.floor(x / 10)) {
        if (x % 10 === 6) {
            maxBase = base;
        }
        base *= 10;
    }
    return num + maxBase * 3;
};

###rust

impl Solution {
    pub fn maximum69_number(num: i32) -> i32 {
        let mut max_base = 0;
        let mut base = 1;
        let mut x = num;
        while x > 0 {
            if x % 10 == 6 {
                max_base = base;
            }
            base *= 10;
            x /= 10;
        }
        num + max_base * 3
    }
}

复杂度分析

  • 时间复杂度：$\mathcal{O}(\log \textit{num})$。
  • 空间复杂度：$\mathcal{O}(1)$。

思考题

  1. 改成求最小数字。
  2. 额外输入一个正整数 $k$，至多翻转 $k$ 个数，返回可以得到的最大数字。
  3. 给定正整数 $\textit{low}$ 和 $\textit{high}$，计算闭区间 $[\textit{low},\textit{high}]$ 中的所有整数 $x$ 的 $\texttt{maximum69Number}(x)$ 之和。

欢迎在评论区分享你的思路/代码。

专题训练

见下面贪心题单的「§3.1 字典序最小/最大」。

分类题单

如何科学刷题？

  1. 滑动窗口与双指针（定长/不定长/单序列/双序列/三指针/分组循环）
  2. 二分算法（二分答案/最小化最大值/最大化最小值/第K小）
  3. 单调栈（基础/矩形面积/贡献法/最小字典序）
  4. 网格图（DFS/BFS/综合应用）
  5. 位运算（基础/性质/拆位/试填/恒等式/思维）
  6. 图论算法（DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流）
  7. 动态规划（入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望）
  8. 常用数据结构（前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树）
  9. 数学算法（数论/组合/概率期望/博弈/计算几何/随机算法）
  10. 贪心与思维（基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造）
  11. 链表、二叉树与回溯（前后指针/快慢指针/DFS/BFS/直径/LCA/一般树）
  12. 字符串（KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机）

我的题解精选（已分类）

欢迎关注 B站@灵茶山艾府

6 和 9 组成的最大数字

✇LeetCode 每日一题题解
LeetCode-Solution

方法一：贪心 + 字符串

思路与算法

此题要求将一个由数字 $6$ 和 $9$ 构成的十进制数 $\textit{num}$ 进行至多一次 $6$ 和 $9$ 之间的翻转得到的最大数字。由十进制数的性质易知：贪心的选择数位最高的一个 $6$ 变成 $9$，得到的答案就是最大的。如果不存在这样的 $6$，则说明这个数字全由数字 $9$ 构成。根据题意，此时不对 $\textit{num}$ 做任何更改即为最优解。

对于算法实现，我们使用字符数组来处理 $\textit{num}$ 较为方便。首先将 $\textit{num}$ 转为字符数组，然后从左到遍历字符，按上述算法处理。最后将修改后的字符数组转回数字即为所求。

代码

###C++

class Solution {
public:
    int maximum69Number (int num) {
        string s = to_string(num);
        for (char &c : s) {
            if (c == '6') {
                c = '9';
                break;
            }
        }
        return stoi(s);
    }
};

###Java

public class Solution {
    public int maximum69Number (int num) {
        char[] chars = Integer.toString(num).toCharArray();
        for (int i = 0; i < chars.length; i++) {
            if (chars[i] == '6') {
                chars[i] = '9';
                break;
            }
        }
        return Integer.parseInt(new String(chars));
    }
}

###C#

public class Solution {
    public int Maximum69Number (int num) {
        char[] chars = num.ToString().ToCharArray();
        for (int i = 0; i < chars.Length; i++) {
            if (chars[i] == '6') {
                chars[i] = '9';
                break;
            }
        }
        return int.Parse(new string(chars));
    }
}

###Go

func maximum69Number(num int) int {
    s := strconv.Itoa(num)
    chars := []byte(s)
    for i := 0; i < len(chars); i++ {
        if chars[i] == '6' {
            chars[i] = '9'
            break
        }
    }
    result, _ := strconv.Atoi(string(chars))
    return result
}

###Python

class Solution:
    def maximum69Number (self, num: int) -> int:
        s = list(str(num))
        for i in range(len(s)):
            if s[i] == '6':
                s[i] = '9'
                break
        return int(''.join(s))

###C

int maximum69Number(int num) {
    char s[20];
    sprintf(s, "%d", num);
    for (int i = 0; s[i] != '\0'; i++) {
        if (s[i] == '6') {
            s[i] = '9';
            break;
        }
    }
    return atoi(s);
}

###Rust

impl Solution {
    pub fn maximum69_number (num: i32) -> i32 {
        let mut s = num.to_string().chars().collect::<Vec<char>>();
        for i in 0..s.len() {
            if s[i] == '6' {
                s[i] = '9';
                break;
            }
        }
        s.iter().collect::<String>().parse().unwrap()
    }
}

###JavaScript

var maximum69Number = function (num) {
    let charArray = [...num.toString()];

    for (let i = 0; i < charArray.length; i++) {
        if (charArray[i] === '6') {
            charArray[i] = '9';
            break;
        }
    }

    return Number(charArray.join(''));
};

###TypeScript

function maximum69Number(num: number): number {
    let charArray = [...num.toString()];

    for (let i = 0; i < charArray.length; i++) {
        if (charArray[i] === '6') {
            charArray[i] = '9';
            break;
        }
    }

    return Number(charArray.join(''));
};

复杂度分析

  • 时间复杂度：$O(\log \textit{num})$。

  • 空间复杂度：$O(\log \textit{num})$。

方法二：贪心 + 数学

思路与算法

思想同方法一，但是不依赖字符串操作，而是通过纯数学的方式找到最高位的 $6$ 并更改为 $9$。

首先初始化一个基数 $\textit{digitBase} = 10^{\lfloor \log_{10}(\textit{num}) \rfloor}$，这个基数代表了 $\textit{num}$ 的最高位。然后从高位向低位遍历，每次将 $\textit{digitBase}$ 除以 $10$。在每一次循环中，通过 $\lfloor \textit{num} \div \textit{digitBase} \rfloor \bmod 10$ 来获取当前基数 $\textit{digitBase}$ 所在的十进制位上的数字。一旦这个数字等于 $6$，我们就可以确定这就是需要修改的最高位的 $6$。此时，我们将 $\textit{num}$ 加上 $3 \times \textit{digitBase}$，即可将该位的 $6$ 修改为 $9$，结果即为所求。

代码

###C++

class Solution {
public:
    int maximum69Number (int num) {
        int digitBase = pow(10, (int)log10(num));
        while (digitBase > 0) {
            if ((num / digitBase) % 10 == 6) {
                num += 3 * digitBase;
                return num;
            }
            digitBase /= 10;
        }
        
        return num;
    }
};

###Java

public class Solution {
    public int maximum69Number (int num) {
        int digitBase = (int)Math.pow(10, (int)Math.log10(num));
        while (digitBase > 0) {
            if ((num / digitBase) % 10 == 6) {
                num += 3 * digitBase;
                return num;
            }
            digitBase /= 10;
        }
        
        return num;
    }
}

###C#

public class Solution {
    public int Maximum69Number (int num) {
        int digitBase = (int)Math.Pow(10, (int)Math.Log10(num));
        while (digitBase > 0) {
            if ((num / digitBase) % 10 == 6) {
                num += 3 * digitBase;
                return num;
            }
            digitBase /= 10;
        }
        
        return num;
    }
}

###Go

func maximum69Number(num int) int {
    digitBase := int(math.Pow10(int(math.Log10(float64(num)))))
    for digitBase > 0 {
        if (num / digitBase) % 10 == 6 {
            num += 3 * digitBase
            return num
        }
        digitBase /= 10
    }
    
    return num
}

###Python

class Solution:
    def maximum69Number (self, num: int) -> int:
        digit_base = 10 ** int(math.log10(num)) if num != 0 else 0
        while digit_base > 0:
            if (num // digit_base) % 10 == 6:
                num += 3 * digit_base
                return num
            digit_base = digit_base // 10
        
        return num

###C

int maximum69Number(int num) {
    int digitBase = pow(10, (int)log10(num));
    while (digitBase > 0) {
        if ((num / digitBase) % 10 == 6) {
            num += 3 * digitBase;
            return num;
        }
        digitBase /= 10;
    }
    
    return num;
}

###Rust

impl Solution {
    pub fn maximum69_number (num: i32) -> i32 {
        let mut digit_base = 10i32.pow((num as f32).log10() as u32);
        let mut num = num;
        while digit_base > 0 {
            if (num / digit_base) % 10 == 6 {
                num += 3 * digit_base;
                return num;
            }
            digit_base /= 10;
        }
        
        num
    }
}

###JavaScript

var maximum69Number = function (num) {
    let digitBase = Math.pow(10, Math.trunc(Math.log10(num)));

    while (digitBase > 0) {
        if (Math.trunc(num / digitBase) % 10 === 6) {
            num += 3 * digitBase;
            return num;
        }
        digitBase = Math.trunc(digitBase / 10);
    }

    return num;
};

###TypeScript

function maximum69Number(num: number): number {
    let digitBase = Math.pow(10, Math.trunc(Math.log10(num)));

    while (digitBase > 0) {
        if (Math.trunc(num / digitBase) % 10 === 6) {
            num += 3 * digitBase;
            return num;
        }
        digitBase = Math.trunc(digitBase / 10);
    }

    return num;
};

复杂度分析

  • 时间复杂度：$O(\log \textit{num})$。

  • 空间复杂度：$O(1)$。

C 不转换字符串

✇LeetCode 每日一题题解
logan-31

解题思路

循环看看哪个6最靠前，然后加上3的x次幂即可
（4ms, 61.64%; 6.8MB, 100.00%）

代码

###c

#include <Math.h>
int maximum69Number (int num){
    int count = 0, th = 0;          // count 记录除了多少次，th记录最大的6在第几位
    int re = num;
    while(re){
        count++;
        if(re%10==6)
           th = count;
        re /= 10;
    }
    return num+3*pow(10,th-1);
}

每日一题-判断一个数字是否可以表示成三的幂的和🟡

✇LeetCode 每日一题题解

给你一个整数 n ，如果你可以将 n 表示成若干个不同的三的幂之和，请你返回 true ，否则请返回 false 。

对于一个整数 y ，如果存在整数 x 满足 y == 3x ，我们称这个整数 y 是三的幂。

 

示例 1：

输入：n = 12
输出：true
解释：12 = 31 + 32

示例 2：

输入：n = 91
输出：true
解释：91 = 30 + 32 + 34

示例 3：

输入：n = 21
输出：false

 

提示：

  • 1 <= n <= 107

【爪哇缪斯】图解LeetCode

✇LeetCode 每日一题题解
muse-77

解题思路

根据题目表述，我们要判断n是否满足三的幂之和，其实关于这道题，如果我们将三的幂之和改变为二的幂之和，就清晰多了。因为我们常用的二进制转成十进制，就是采用二的幂之和来计算获得了。那么，同理，我们采用三进制计算的方式，就可以获得这道题的答案了。

也就是说，我们通过对n进行除3取余操作，如果获得0或1，则表示满足三进制，依次类推，直到除完为止。如果在除3取余过程中，不满足0或者1，则直接返回false。具体逻辑，请参照下图所示：

image.png

代码实现

###java

class Solution {
    public boolean checkPowersOfThree(int n) {
        while (n != 0) {
            if (n % 3 == 0 || n % 3 == 1) n = n / 3; // 满足三进制
            else return false; // 不满足三进制，返回false
        }
        return true;
    }
}

image.png

今天的文章内容就这些了：

写作不易，笔者几个小时甚至数天完成的一篇文章，只愿换来您几秒钟的 点赞 & 分享 。

更多技术干货，欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享，每天更新」

三进制

✇LeetCode 每日一题题解
himymBen

Problem: 1780. 判断一个数字是否可以表示成三的幂的和

[TOC]

思路

一个数可以表示为不同的3的幂次的和，那么它的三进制每一位只能是1或0

解题方法

按三进制转换，确保三进制任意位中没有2

复杂度

  • 时间复杂度:

$O(log_{3}n)$

  • 空间复杂度:

$O(1)$

Code

###Python3


class Solution:
    def checkPowersOfThree(self, n: int) -> bool:
        while n:
            if n % 3 == 2:
                return False
            n //= 3
        return True

###Go

func checkPowersOfThree(n int) bool {
    for ; n > 0; n /= 3 {
        if n % 3 == 2 {
            return false
        }
    }
    return true
}

判断一个数字是否可以表示成三的幂的和

✇LeetCode 每日一题题解
LeetCode-Solution

方法一：进制转换

思路与算法

我们可以将 $n$ 转换成 $3$ 进制。如果 $n$ 的 $3$ 进制表示中每一位均不为 $2$，那么答案为 $\text{True}$，否则为 $\text{False}$。

例如当 $n=12$ 时，$12 = (110)_3$，满足要求；当 $n=21$ 时，$21 = (210)_3$，不满足要求。

代码

###C++

class Solution {
public:
    bool checkPowersOfThree(int n) {
        while (n) {
            if (n % 3 == 2) {
                return false;
            }
            n /= 3;
        }
        return true;
    }
};

###Java

class Solution {
    public boolean checkPowersOfThree(int n) {
        while (n != 0) {
            if (n % 3 == 2) {
                return false;
            }
            n /= 3;
        }
        return true;
    }
}

###C#

public class Solution {
    public bool CheckPowersOfThree(int n) {
        while (n != 0) {
            if (n % 3 == 2) {
                return false;
            }
            n /= 3;
        }
        return true;
    }
}

###Python

class Solution:
    def checkPowersOfThree(self, n: int) -> bool:
        while n > 0:
            if n % 3 == 2:
                return False
            n //= 3
        return True

###C

bool checkPowersOfThree(int n) {
    while (n) {
        if (n % 3 == 2) {
            return false;
        }
        n /= 3;
    }
    return true;
}

###JavaScript

var checkPowersOfThree = function(n) {
    while (n !== 0) {
        if (n % 3 === 2) {
            return false;
        }
        n = Math.floor(n / 3);
    }
    return true;
};

###go

func checkPowersOfThree(n int) bool {
    for ; n > 0; n /= 3 {
        if n%3 == 2 {
            return false
        }
    }
    return true
}

复杂度分析

  • 时间复杂度：$O(\log n)$，即为进制转换需要的时间。

  • 空间复杂度：$O(1)$。

每日一题-3 的幂🟢

✇LeetCode 每日一题题解

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。

整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x

 

示例 1：

输入：n = 27
输出：true

示例 2：

输入：n = 0
输出：false

示例 3：

输入：n = 9
输出：true

示例 4：

输入：n = 45
输出：false

 

提示：

  • -231 <= n <= 231 - 1

 

进阶：你能不使用循环或者递归来完成本题吗？

O(1) 数学做法，一行搞定（Python/Java/C++/C/Go/JS/Rust）

✇LeetCode 每日一题题解
endlesscheng

$3$ 的幂一定大于 $0$。如果 $n\le 0$，那么 $n$ 不是 $3$ 的幂。下文假定 $n>0$。

在本题的数据范围下，最大的 $3$ 的幂是 $3^{19} = 1162261467$。

怎么算的？比如可以写个循环，找最大的满足 $3^i\le 2^{31}-1$ 的整数 $i$。

  • 如果 $n$ 是 $3$ 的幂。由于任何 $3$ 的幂都是 $3^{19}$ 的因子，所以 $3^{19}\bmod n = 0$。或者说 $n$ 的某个倍数等于 $3^{19}$。
  • 如果 $n$ 不是 $3$ 的幂。那么 $n$ 必然有不等于 $3$ 的质因子，所以 $n$ 的倍数不可能等于 $3^{19}$ 这个只含质因子 $3$ 的数，所以 $3^{19}\bmod n \ne 0$。

因此，在本题数据范围下，当且仅当 $n>0$ 且 $3^{19}\bmod n = 0$ 时，$n$ 是 $3$ 的幂。

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        return n > 0 and 1162261467 % n == 0

class Solution {
    public boolean isPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }
}

class Solution {
public:
    bool isPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }
};

bool isPowerOfThree(int n) {
    return n > 0 && 1162261467 % n == 0;
}

func isPowerOfThree(n int) bool {
    return n > 0 && 1162261467%n == 0
}

var isPowerOfThree = function(n) {
    return n > 0 && 1162261467 % n === 0;
};

impl Solution {
    pub fn is_power_of_three(n: i32) -> bool {
        n > 0 && 1162261467 % n == 0
    }
}

复杂度分析

  • 时间复杂度：$\mathcal{O}(1)$。
  • 空间复杂度：$\mathcal{O}(1)$。

分类题单

如何科学刷题？

  1. 滑动窗口与双指针（定长/不定长/单序列/双序列/三指针/分组循环）
  2. 二分算法（二分答案/最小化最大值/最大化最小值/第K小）
  3. 单调栈（基础/矩形面积/贡献法/最小字典序）
  4. 网格图（DFS/BFS/综合应用）
  5. 位运算（基础/性质/拆位/试填/恒等式/思维）
  6. 图论算法（DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流）
  7. 动态规划（入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望）
  8. 常用数据结构（前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树）
  9. 数学算法（数论/组合/概率期望/博弈/计算几何/随机算法）
  10. 贪心与思维（基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造）
  11. 链表、二叉树与回溯（前后指针/快慢指针/DFS/BFS/直径/LCA/一般树）
  12. 字符串（KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机）

我的题解精选（已分类）

欢迎关注 B站@灵茶山艾府

【宫水三叶】一题三解 :「数学」&「倍数/约数」&「打表」

✇LeetCode 每日一题题解
AC_OIer

数学

一个不能再朴素的做法是将 $n$ 对 $3$ 进行试除，直到 $n$ 不再与 $3$ 呈倍数关系，最后判断 $n$ 是否为 $3^0 = 1$ 即可。

代码：

###Java

class Solution {
    public boolean isPowerOfThree(int n) {
        if (n <= 0) return false;
        while (n % 3 == 0) n /= 3;
        return n == 1;
    }
}
  • 时间复杂度：$O(\log_{3}n)$
  • 空间复杂度：$O(1)$

倍数 & 约数

题目要求不能使用循环或递归来做，而传参 $n$ 的数据类型为 int，这引导我们首先分析出 int 范围内的最大 $3$ 次幂是多少，约为 $3^{19} = 1162261467$。

如果 $n$ 为 $3$ 的幂的话，那么必然满足 $n * 3^k = 1162261467$，即 $n$ 与 $1162261467$ 存在倍数关系。

因此，我们只需要判断 $n$ 是否为 $1162261467$ 的约数即可。

注意：这并不是快速判断 $x$ 的幂的通用做法，当且仅当 $x$ 为质数可用。

代码：

###Java

class Solution {
    public boolean isPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }
}
  • 时间复杂度：$O(1)$
  • 空间复杂度：$O(1)$

打表

另外一个更容易想到的「不使用循环/递归」的做法是进行打表预处理。

使用 static 代码块，预处理出不超过 int 数据范围的所有 $3$ 的幂，这样我们在跑测试样例时，就不需要使用「循环/递归」来实现逻辑，可直接 $O(1)$ 查表返回。

代码：

###Java

class Solution {
    static Set<Integer> set = new HashSet<>();
    static {
        int cur = 1;
        set.add(cur);
        while (cur <= Integer.MAX_VALUE / 3) {
            cur *= 3;
            set.add(cur);
        }
    }
    public boolean isPowerOfThree(int n) {
        return n > 0 && set.contains(n);
    }
}
  • 时间复杂度：将打表逻辑交给 $OJ$ 执行的话，复杂度为 $O(\log_3{C})$，$C$ 固定为 $2147483647$；将打表逻辑放到本地执行，复杂度为 $O(1)$
  • 空间复杂度：$O(\log_3{n})$

其他「$x$ 的幂」问题

题目简单？不如来看「矩阵快速幂」三部曲 🍭🍭🍭：

题目 题解 难度 推荐指数
1137. 第 N 个泰波那契数 LeetCode 题解链接 简单 🤩🤩🤩🤩🤩
剑指 Offer 10- I. 斐波那契数列 LeetCode 题解链接 简单 🤩🤩🤩🤩🤩
552. 学生出勤记录 II LeetCode 题解链接 困难 🤩🤩🤩🤩

或是加练如下的「$x$ 的幂」问题 🍭🍭🍭：

题目 题解 难度 推荐指数
231. 2 的幂 LeetCode 题解链接 简单 🤩🤩🤩🤩
342. 4的幂 LeetCode 题解链接 简单 🤩🤩🤩🤩

最后

如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ ("▔□▔)/

也欢迎你 关注我（公主号后台回复「送书」即可参与长期看题解学算法送实体书活动）或 加入「组队打卡」小群 ，提供写「证明」&「思路」的高质量题解。

所有题解已经加入 刷题指南，欢迎 star 哦 ~

3的幂

✇LeetCode 每日一题题解
LeetCode-Solution

方法一：试除法

思路与算法

我们不断地将 $n$ 除以 $3$，直到 $n=1$。如果此过程中 $n$ 无法被 $3$ 整除，就说明 $n$ 不是 $3$ 的幂。

本题中的 $n$ 可以为负数或 $0$，可以直接提前判断该情况并返回 $\text{False}$，也可以进行试除，因为负数或 $0$ 也无法通过多次除以 $3$ 得到 $1$。

代码

###C++

class Solution {
public:
    bool isPowerOfThree(int n) {
        while (n && n % 3 == 0) {
            n /= 3;
        }
        return n == 1;
    }
};

###Java

class Solution {
    public boolean isPowerOfThree(int n) {
        while (n != 0 && n % 3 == 0) {
            n /= 3;
        }
        return n == 1;
    }
}

###C#

public class Solution {
    public bool IsPowerOfThree(int n) {
        while (n != 0 && n % 3 == 0) {
            n /= 3;
        }
        return n == 1;
    }
}

###Python

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        while n and n % 3 == 0:
            n //= 3
        return n == 1

###JavaScript

var isPowerOfThree = function(n) {
    while (n !== 0 && n % 3 === 0) {
        n = Math.floor(n / 3);
    }
    return n === 1;
};

###go

func isPowerOfThree(n int) bool {
    for n > 0 && n%3 == 0 {
        n /= 3
    }
    return n == 1
}

复杂度分析

  • 时间复杂度：$O(\log n)$。当 $n$ 是 $3$ 的幂时，需要除以 $3$ 的次数为 $\log_3 n = O(\log n)$；当 $n$ 不是 $3$ 的幂时，需要除以 $3$ 的次数小于该值。

  • 空间复杂度：$O(1)$。

方法二：判断是否为最大 $3$ 的幂的约数

思路与算法

我们还可以使用一种较为取巧的做法。

在题目给定的 $32$ 位有符号整数的范围内，最大的 $3$ 的幂为 $3^{19} = 1162261467$。我们只需要判断 $n$ 是否是 $3^{19}$ 的约数即可。

与方法一不同的是，这里需要特殊判断 $n$ 是负数或 $0$ 的情况。

代码

###C++

class Solution {
public:
    bool isPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }
};

###Java

class Solution {
    public boolean isPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }
}

###C#

public class Solution {
    public bool IsPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }
}

###Python

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        return n > 0 and 1162261467 % n == 0

###JavaScript

var isPowerOfThree = function(n) {
    return n > 0 && 1162261467 % n === 0;
};

###go

func isPowerOfThree(n int) bool {
    return n > 0 && 1162261467%n == 0
}

复杂度分析

  • 时间复杂度：$O(1)$。

  • 空间复杂度：$O(1)$。

每日一题-将一个数字表示成幂的和的方案数🟡

✇LeetCode 每日一题题解

给你两个 正 整数 n 和 x 。

请你返回将 n 表示成一些 互不相同 正整数的 x 次幂之和的方案数。换句话说，你需要返回互不相同整数 [n1, n2, ..., nk] 的集合数目，满足 n = n1x + n2x + ... + nkx 。

由于答案可能非常大，请你将它对 109 + 7 取余后返回。

比方说，n = 160 且 x = 3 ，一个表示 n 的方法是 n = 23 + 33 + 53 。

 

示例 1：

输入：n = 10, x = 2
输出：1
解释：我们可以将 n 表示为：n = 32 + 12 = 10 。
这是唯一将 10 表达成不同整数 2 次方之和的方案。

示例 2：

输入：n = 4, x = 1
输出：2
解释：我们可以将 n 按以下方案表示：
- n = 41 = 4 。
- n = 31 + 11 = 4 。

 

提示：

  • 1 <= n <= 300
  • 1 <= x <= 5

2787. 将一个数字表示成幂的和的方案数

✇LeetCode 每日一题题解
stormsunshine

解法

思路和算法

计算 $\textit{maxNum} = \lfloor \sqrt[x]{n} \rfloor$，则当 $n$ 表示成各不相同的正整数的 $x$ 次幂之和时，任何一个作为底数的正整数都不能超过 $\textit{maxNum}$。问题等价于计算从 $1^x$ 到 $\textit{maxNum}^x$ 的 $\textit{maxNum}$ 个正整数的 $x$ 次幂中选取一个或多个数字满足选取的数字之和等于 $n$ 的方案数。

该问题是 0-1 背包问题的变种，和传统 0-1 背包问题的区别在于，这道题要求选取的数字之和恰好等于 $n$。对于每个数字，选取的数字之和取决于之前选取的数字，因此可以使用动态规划计算选取的数字之和等于 $n$ 的方案数。

创建 $(\textit{maxNum} + 1) \times (n + 1)$ 的二维数组 $\textit{dp}$，其中 $\textit{dp}[i][j]$ 表示在前 $i$ 个数字中选取数字使数字之和等于 $j$ 的方案数。

当 $i = 0$ 时，没有任何数字，数字之和一定是 $0$，因此动态规划的边界情况是：当 $j = 0$ 时 $\textit{dp}[0][j] = 1$，当 $j > 0$ 时 $\textit{dp}[0][j] = 0$。

当 $i > 0$ 时，当前数字是 $i^x$，只有当 $j \ge i^x$ 时才能选取当前数字。分别考虑 $j < i^x$ 和 $j \ge i^x$ 的情况。

  • 如果 $j < i^x$，则不能选取当前数字，在前 $i$ 个数字中选取数字使数字之和等于 $j$ 等价于在前 $i - 1$ 个数字中选取数字使数字之和等于 $j$，因此方案数为 $\textit{dp}[i - 1][j]$。

  • 如果 $j \ge i^x$，则可以不选取或选取当前数字，根据两种情况计算方案数。

    • 如果不选取当前数字，则需要在前 $i - 1$ 个数字中选取数字使数字之和等于 $j$，方案数为 $\textit{dp}[i - 1][j]$。

    • 如果选取当前数字，则需要在前 $i - 1$ 个数字中选取数字使数字之和等于 $j - i^x$，加上选取的当前数字之后数字之和等于 $j$，因此方案数为 $\textit{dp}[i - 1][j - i^x]$。

因此动态规划的状态转移方程如下。

  • 如果 $j < i^x$，则 $\textit{dp}[i][j] = \textit{dp}[i - 1][j]$。

  • 如果 $j \ge i^x$，则 $\textit{dp}[i][j] = \textit{dp}[i - 1][j] + \textit{dp}[i - 1][j - i^x]$。

根据动态规划的状态转移方程，计算 $\textit{dp}[i][j]$ 的顺序为从小到大遍历每个 $i$。计算得到 $\textit{dp}[\textit{maxNum}][n]$ 即为将 $n$ 表示成各不相同的正整数的 $x$ 次幂之和的方案数。

上述做法的时间复杂度和空间复杂度都是 $O(\sqrt[x]{n} \times n)$。

实现方面可以优化空间，做法如下。

  1. 由于 $\textit{dp}[i][]$ 只取决于 $\textit{dp}[i - 1][]$，和更早的状态无关，因此可以使用滚动数组的思想，只保留前一个 $i$ 处的状态，将空间复杂度降到 $O(n)$。

  2. 优化空间时，如果从小到大遍历每个 $j$ 则对于每个遍历到的 $i$ 都需要新建一个临时数组。可以进一步优化空间，从大到小遍历每个 $j$，则不需要新建临时数组。

为了避免浮点数误差，计算 $\textit{maxNum}$ 时可以取 $\textit{maxNum} = \lfloor \sqrt[x]{n + 0.5} \rfloor$。

代码

下面的代码为不优化空间的实现。

###Java

class Solution {
    static final int MODULO = 1000000007;

    public int numberOfWays(int n, int x) {
        int maxNum = (int) Math.pow(n + 0.5, 1.0 / x);
        int[][] dp = new int[maxNum + 1][n + 1];
        dp[0][0] = 1;
        for (int i = 1; i <= maxNum; i++) {
            int power = (int) Math.pow(i, x);
            for (int j = 0; j <= n; j++) {
                if (j < power) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = (dp[i - 1][j] + dp[i - 1][j - power]) % MODULO;
                }
            }
        }
        return dp[maxNum][n];
    }
}

###C#

public class Solution {
    const int MODULO = 1000000007;

    public int NumberOfWays(int n, int x) {
        int maxNum = (int) Math.Pow(n + 0.5, 1.0 / x);
        int[][] dp = new int[maxNum + 1][];
        for (int i = 0; i <= maxNum; i++) {
            dp[i] = new int[n + 1];
        }
        dp[0][0] = 1;
        for (int i = 1; i <= maxNum; i++) {
            int power = (int) Math.Pow(i, x);
            for (int j = 0; j <= n; j++) {
                if (j < power) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = (dp[i - 1][j] + dp[i - 1][j - power]) % MODULO;
                }
            }
        }
        return dp[maxNum][n];
    }
}

下面的代码为优化空间的实现。

###Java

class Solution {
    static final int MODULO = 1000000007;

    public int numberOfWays(int n, int x) {
        int maxNum = (int) Math.pow(n + 0.5, 1.0 / x);
        int[] dp = new int[n + 1];
        dp[0] = 1;
        for (int i = 1; i <= maxNum; i++) {
            int power = (int) Math.pow(i, x);
            for (int j = n; j >= power; j--) {
                dp[j] = (dp[j] + dp[j - power]) % MODULO;
            }
        }
        return dp[n];
    }
}

###C#

public class Solution {
    const int MODULO = 1000000007;

    public int NumberOfWays(int n, int x) {
        int maxNum = (int) Math.Pow(n + 0.5, 1.0 / x);
        int[] dp = new int[n + 1];
        dp[0] = 1;
        for (int i = 1; i <= maxNum; i++) {
            int power = (int) Math.Pow(i, x);
            for (int j = n; j >= power; j--) {
                dp[j] = (dp[j] + dp[j - power]) % MODULO;
            }
        }
        return dp[n];
    }
}

复杂度分析

代码中使用了 $\texttt{Math.pow}$ 方法，该方法调用了本地方法 $\texttt{StrictMath.pow}$，因此其时间与空间复杂度取决于本地方法的实现，此处的复杂度分析将该方法的时间复杂度和空间复杂度视为 $O(1)$。

  • 时间复杂度：$O(\sqrt[x]{n} \times n)$，其中 $n$ 和 $x$ 是给定的正整数。状态数是 $O(\sqrt[x]{n} \times n)$，每个状态的计算时间是 $O(1)$，因此时间复杂度是 $O(\sqrt[x]{n} \times n)$。

  • 空间复杂度：$O(\sqrt[x]{n} \times n)$ 或 $O(n)$，其中 $n$ 和 $x$ 是给定的正整数。空间复杂度取决于实现方式，不优化空间的实现需要创建大小为 $(\lfloor \sqrt[x]{n} \rfloor + 1) \times (n + 1)$ 的二维数组因此空间复杂度是 $O(\sqrt[x]{n} \times n)$，优化空间的实现需要创建长度为 $n + 1$ 的一维数组因此空间复杂度是 $O(n)$。

0-1 背包模板题（Python/Java/C++/C/Go/JS/Rust）

✇LeetCode 每日一题题解
endlesscheng

把 $n$ 看成背包容量，$1^x,2^x,3^x,\dots$ 看成物品，本题是恰好装满型 0-1 背包的方案数，做法同 494. 目标和，原理讲解见【基础算法精讲 18】，包含倒序循环的讲解。

代码实现时，由于最坏情况 $n=300$，$x=1$ 的答案没有超过 $64$ 位整数的最大值，可以在计算结束后再取模。

class Solution:
    def numberOfWays(self, n: int, x: int) -> int:
        f = [1] + [0] * n
        for i in range(1, n + 1):
            v = i ** x
            if v > n:
                break
            for s in range(n, v - 1, -1):
                f[s] += f[s - v]
        return f[n] % 1_000_000_007

# 预处理所有答案
MX_N = 300
MX_X = 5
f = [[1] + [0] * MX_N for _ in range(MX_X + 1)]
for x in range(1, MX_X + 1):
    for i in count(1):
        v = i ** x
        if v > MX_N:
            break
        for s in range(MX_N, v - 1, -1):
            f[x][s] += f[x][s - v]

class Solution:
    def numberOfWays(self, n: int, x: int) -> int:
        return f[x][n] % 1_000_000_007

class Solution {
    int numberOfWays(int n, int x) {
        long[] f = new long[n + 1];
        f[0] = 1;
        // 本题数据范围小，Math.pow 的计算结果一定准确
        for (int i = 1; Math.pow(i, x) <= n; i++) {
            int v = (int) Math.pow(i, x);
            for (int s = n; s >= v; s--) {
                f[s] += f[s - v];
            }
        }
        return (int) (f[n] % 1_000_000_007);
    }
}

class Solution {
public:
    int numberOfWays(int n, int x) {
        vector<long long> f(n + 1);
        f[0] = 1;
        // 本题数据范围小，pow 的计算结果一定准确
        for (int i = 1; pow(i, x) <= n; i++) {
            int v = pow(i, x);
            for (int s = n; s >= v; s--) {
                f[s] += f[s - v];
            }
        }
        return f[n] % 1'000'000'007;
    }
};

#define MOD 1000000007

int numberOfWays(int n, int x) {
    long long* f = calloc(n + 1, sizeof(long long));
    f[0] = 1;

    // 本题数据范围小，pow 的计算结果一定准确
    for (int i = 1; pow(i, x) <= n; i++) {
        int v = pow(i, x);
        for (int s = n; s >= v; s--) {
            f[s] += f[s - v];
        }
    }

    int ans = f[n] % MOD;
    free(f);
    return ans;
}

func numberOfWays(n, x int) int {
f := make([]int, n+1)
f[0] = 1
for i := 1; pow(i, x) <= n; i++ {
v := pow(i, x)
for s := n; s >= v; s-- {
f[s] += f[s-v]
}
}
return f[n] % 1_000_000_007
}

// 本题数据范围小，math.Pow 的计算结果一定准确
func pow(i, x int) int {
return int(math.Pow(float64(i), float64(x)))
}

var numberOfWays = function(n, x) {
    const f = new Array(n + 1).fill(0);
    f[0] = 1;
    // 本题数据范围小，pow 的计算结果一定准确
    for (let i = 1; Math.pow(i, x) <= n; i++) {
        const v = Math.pow(i, x);
        for (let s = n; s >= v; s--) {
            f[s] += f[s - v];
        }
    }
    return f[n] % 1_000_000_007;
};

impl Solution {
    pub fn number_of_ways(n: i32, x: i32) -> i32 {
        let n = n as usize;
        let mut f = vec![0i64; n + 1];
        f[0] = 1;
        for i in 1usize.. {
            let v = i.pow(x as u32);
            if v > n {
                break;
            }
            for s in (v..=n).rev() {
                f[s] += f[s - v];
            }
        }
        (f[n] % 1_000_000_007) as _
    }
}

复杂度分析

  • 时间复杂度：$\mathcal{O}(n\sqrt[x]n)$。外层循环的循环次数为 $\mathcal{O}(\sqrt[x]n)$。
  • 空间复杂度：$\mathcal{O}(n)$。

注：也可以用快速幂计算 $\texttt{pow}$，原理见【图解】一张图秒懂快速幂。

专题训练

见下面动态规划题单的「§3.1 0-1 背包」。

分类题单

如何科学刷题？

  1. 滑动窗口与双指针（定长/不定长/单序列/双序列/三指针/分组循环）
  2. 二分算法（二分答案/最小化最大值/最大化最小值/第K小）
  3. 单调栈（基础/矩形面积/贡献法/最小字典序）
  4. 网格图（DFS/BFS/综合应用）
  5. 位运算（基础/性质/拆位/试填/恒等式/思维）
  6. 图论算法（DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流）
  7. 动态规划（入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望）
  8. 常用数据结构（前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树）
  9. 数学算法（数论/组合/概率期望/博弈/计算几何/随机算法）
  10. 贪心与思维（基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造）
  11. 链表、二叉树与回溯（前后指针/快慢指针/DFS/BFS/直径/LCA/一般树）
  12. 字符串（KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机）

我的题解精选（已分类）

欢迎关注 B站@灵茶山艾府

❌