方法一:子树的序列化表示
思路
我们可以想出这道题在抽象层面(也就是省去了所有实现细节)的解决方法,即:
-
第一步,我们通过给定的 $\textit{paths}$,简历出文件系统的树型表示。这棵树是一棵多叉树,根节点为 $\texttt{/}$,每个非根节点表示一个文件夹。
-
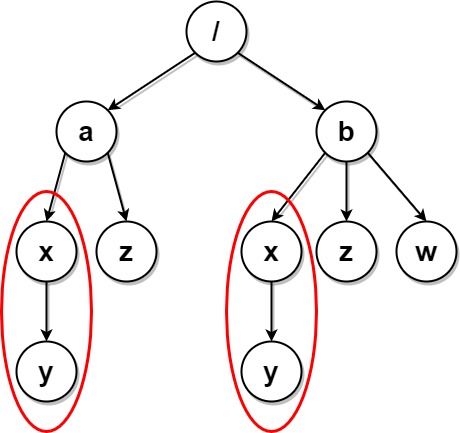
第二步,我们对整棵树从根节点开始进行一次遍历。根据题目中的描述,如果两个节点 $x$ 和 $y$ 包含的子文件夹的「结构」(即这些子文件夹、子文件夹的子文件夹等等,递归直到空文件夹为止)完全相同,我们就需要将 $x$ 和 $y$ 都进行删除。那么,为了得到某一个节点的子文件夹的「结构」,我们应当首先遍历完成该节点的所有子节点,再回溯遍历该节点本身。这就对应着多叉树的后序遍历。
在回溯到某节点时,我们需要将该节点的「结构」存储下来,记录在某一「数据结构」中,以便于与其它节点的「结构」进行比较。
-
第三步,我们再次对整棵树从根节点开始进行一次遍历。当我们遍历到节点 $x$ 时,如果 $x$ 的「结构」在「数据结构」中出现了超过 $1$ 次,那就说明存在于 $x$ 相同的文件夹,我们就需要将 $x$ 删除并回溯,否则 $x$ 是唯一的,我们将从根节点开始到 $x$ 的路径计入答案,并继续向下遍历 $x$ 的子节点。
在遍历完成后,我们就删除了所有重复的文件夹,并且得到了最终的答案。
算法
对于上面的三个步骤,我们依次尝试进行解决。
对于第一步而言,我们只需要定义一个表示树结构的类,建立一个根节点,随后遍历 $\textit{paths}$ 中的每一条表示文件夹的路径,将路径上的所有节点加入树中即可。如果读者已经掌握了字典树(Trie)这一数据结构,就可以较快地实现这一步。
对于第二步而言,难点不在于对树进行后序遍历,而在于如何表示一个节点的「结构」。我们可以参考「297. 二叉树的序列化与反序列化」,实现一个多叉树的序列化表示。我们用 $\text{serial}(x)$ 记录节点 $x$ 的序列化表示,具体地:
-
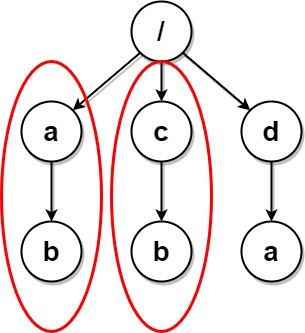
如果节点 $x$ 是子节点,那么 $\text{serial}(x)$ 为空字符串,这是因为节点 $x$ 中不包含任何文件夹,它没有「结构」。例如示例 $1$ 中,三个叶节点 $b, a, a$ 对应的序列化表示均为空字符串;
-
如果节点 $x$ 不是子节点,它的子节点分别为 $y_1, y_2, \cdots, y_k$ 那么 $\text{serial}(x)$ 递归定义为:
$$
\text{serial}(x) = y_1(\text{serial}(y_1))y_2(\text{serial}(y_2))\cdots y_k(\text{serial}(y_k))
$$
也就是说,我们首先递归地求出 $y_1, y_2, \cdots, y_k$ 的序列化表示,随后将它们连通本身的文件夹名拼接在一起,并在外层使用括号 $()$ 将它们之间进行区分(或者说隔离)。但如果只是随意地进行拼接,会产生顺序的问题,即如果有节点 $x_1$ 和 $x_2$,它们有相同的子节点 $y_1$ 和 $y_2$,但在 $x_1$ 的子节点中 $y_1$ 先出现 $y_2$ 后出现,而在 $x_2$ 的子节点中 $y_2$ 先出现而 $y_1$ 后出现,这样尽管 $x_1$ 和 $x_2$ 的「结构」是完全相同的,但会因为子节点的出现顺序不同,导致序列化的字符串不同。
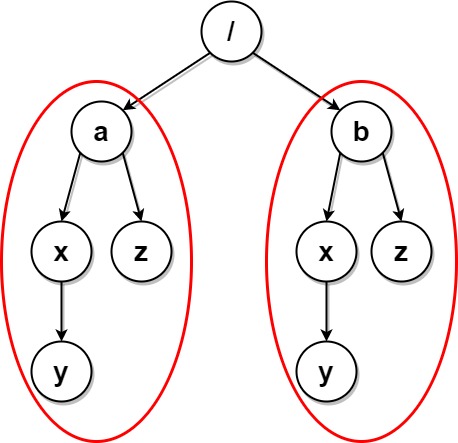
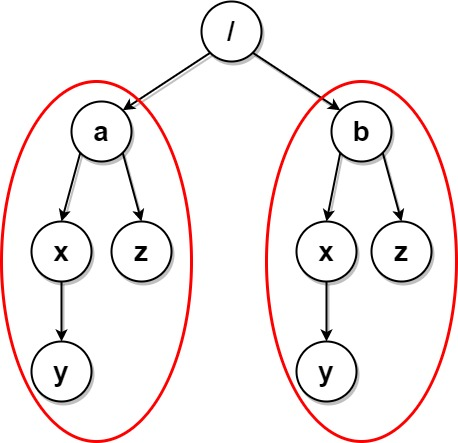
因此,在将 $y_1, y_2, \cdots, y_k$ 的序列化表示进行拼接之前,我们可以对它们进行排序(字典序顺序),再将排序后的结果进行拼接,就可以保证具有相同「结构」的节点的序列化表示是完全相同的了。例如示例 $4$ 中,根节点下方的两个子节点 $a, b$,它们的序列化表示均为 $\texttt{x(y())z()}$。
这样一来,通过一次树的后序遍历,我们就可以求出每一个节点「结构」的序列化表示。由于序列化表示都是字符串,因此我们可以使用一个哈希映射,记录每一种序列化表示以及其对应的出现次数。
对于第三步而言,我们从根节点开始对树进行深度优先遍历,并使用一个数组 $\textit{path}$ 记录从根节点到当前遍历到的节点 $x$ 的路径。如果 $x$ 的序列化表示在哈希映射中出现了超过 $1$ 次,就进行回溯,否则将 $\textit{path}$ 加入答案,并向下递归遍历 $x$ 的所有子节点。
代码
下面的 $\texttt{C++}$ 代码没有析构树的空间。如果在面试中遇到了本题,可以和面试官进行沟通,询问是否需要析构对应的空间。
###C++
struct Trie {
// 当前节点结构的序列化表示
string serial;
// 当前节点的子节点
unordered_map<string, Trie*> children;
};
class Solution {
public:
vector<vector<string>> deleteDuplicateFolder(vector<vector<string>>& paths) {
// 根节点
Trie* root = new Trie();
for (const vector<string>& path: paths) {
Trie* cur = root;
for (const string& node: path) {
if (!cur->children.count(node)) {
cur->children[node] = new Trie();
}
cur = cur->children[node];
}
}
// 哈希表记录每一种序列化表示的出现次数
unordered_map<string, int> freq;
// 基于深度优先搜索的后序遍历,计算每一个节点结构的序列化表示
function<void(Trie*)> construct = [&](Trie* node) {
// 如果是叶节点,那么序列化表示为空字符串,无需进行任何操作
if (node->children.empty()) {
return;
}
vector<string> v;
// 如果不是叶节点,需要先计算子节点结构的序列化表示
for (const auto& [folder, child]: node->children) {
construct(child);
v.push_back(folder + "(" + child->serial + ")");
}
// 防止顺序的问题,需要进行排序
sort(v.begin(), v.end());
for (string& s: v) {
node->serial += move(s);
}
// 计入哈希表
++freq[node->serial];
};
construct(root);
vector<vector<string>> ans;
// 记录根节点到当前节点的路径
vector<string> path;
function<void(Trie*)> operate = [&](Trie* node) {
// 如果序列化表示在哈希表中出现了超过 1 次,就需要删除
if (freq[node->serial] > 1) {
return;
}
// 否则将路径加入答案
if (!path.empty()) {
ans.push_back(path);
}
for (const auto& [folder, child]: node->children) {
path.push_back(folder);
operate(child);
path.pop_back();
}
};
operate(root);
return ans;
}
};
###Python
class Trie:
# 当前节点结构的序列化表示
serial: str = ""
# 当前节点的子节点
children: dict
def __init__(self):
self.children = dict()
class Solution:
def deleteDuplicateFolder(self, paths: List[List[str]]) -> List[List[str]]:
# 根节点
root = Trie()
for path in paths:
cur = root
for node in path:
if node not in cur.children:
cur.children[node] = Trie()
cur = cur.children[node]
# 哈希表记录每一种序列化表示的出现次数
freq = Counter()
# 基于深度优先搜索的后序遍历,计算每一个节点结构的序列化表示
def construct(node: Trie) -> None:
# 如果是叶节点,那么序列化表示为空字符串,无需进行任何操作
if not node.children:
return
v = list()
# 如果不是叶节点,需要先计算子节点结构的序列化表示
for folder, child in node.children.items():
construct(child)
v.append(folder + "(" + child.serial + ")")
# 防止顺序的问题,需要进行排序
v.sort()
node.serial = "".join(v)
# 计入哈希表
freq[node.serial] += 1
construct(root)
ans = list()
# 记录根节点到当前节点的路径
path = list()
def operate(node: Trie) -> None:
# 如果序列化表示在哈希表中出现了超过 1 次,就需要删除
if freq[node.serial] > 1:
return
# 否则将路径加入答案
if path:
ans.append(path[:])
for folder, child in node.children.items():
path.append(folder)
operate(child)
path.pop()
operate(root)
return ans
###Java
class Solution {
class Trie {
String serial; // 当前节点结构的序列化表示
Map<String, Trie> children = new HashMap<>(); // 当前节点的子节点
}
public List<List<String>> deleteDuplicateFolder(List<List<String>> paths) {
Trie root = new Trie(); // 根节点
// 构建字典树
for (List<String> path : paths) {
Trie cur = root;
for (String node : path) {
cur.children.putIfAbsent(node, new Trie());
cur = cur.children.get(node);
}
}
Map<String, Integer> freq = new HashMap<>(); // 哈希表记录每一种序列化表示的出现次数
// 基于深度优先搜索的后序遍历,计算每一个节点结构的序列化表示
construct(root, freq);
List<List<String>> ans = new ArrayList<>();
List<String> path = new ArrayList<>();
// 操作字典树,删除重复文件夹
operate(root, freq, path, ans);
return ans;
}
private void construct(Trie node, Map<String, Integer> freq) {
if (node.children.isEmpty()) return; // 如果是叶节点,无需操作
List<String> v = new ArrayList<>();
for (Map.Entry<String, Trie> entry : node.children.entrySet()) {
construct(entry.getValue(), freq);
v.add(entry.getKey() + "(" + entry.getValue().serial + ")");
}
Collections.sort(v);
StringBuilder sb = new StringBuilder();
for (String s : v) {
sb.append(s);
}
node.serial = sb.toString();
freq.put(node.serial, freq.getOrDefault(node.serial, 0) + 1);
}
private void operate(Trie node, Map<String, Integer> freq, List<String> path, List<List<String>> ans) {
if (freq.getOrDefault(node.serial, 0) > 1) return; // 如果序列化表示出现超过1次,需要删除
if (!path.isEmpty()) {
ans.add(new ArrayList<>(path));
}
for (Map.Entry<String, Trie> entry : node.children.entrySet()) {
path.add(entry.getKey());
operate(entry.getValue(), freq, path, ans);
path.remove(path.size() - 1);
}
}
}
###C#
public class Solution {
class Trie {
public string Serial { get; set; } = ""; // 当前节点结构的序列化表示
public Dictionary<string, Trie> Children { get; } = new Dictionary<string, Trie>(); // 当前节点的子节点
}
public IList<IList<string>> DeleteDuplicateFolder(IList<IList<string>> paths) {
// 根节点
Trie root = new Trie();
// 构建字典树
foreach (var p in paths) {
Trie current = root;
foreach (var node in p) {
if (!current.Children.ContainsKey(node)) {
current.Children[node] = new Trie();
}
current = current.Children[node];
}
}
// 哈希表记录每一种序列化表示的出现次数
var freq = new Dictionary<string, int>();
// 基于深度优先搜索的后序遍历,计算每一个节点结构的序列化表示
void Construct(Trie node) {
// 如果是叶节点,那么序列化表示为空字符串,无需进行任何操作
if (node.Children.Count == 0) {
return;
}
var v = new List<string>();
// 如果不是叶节点,需要先计算子节点结构的序列化表示
foreach (var entry in node.Children) {
Construct(entry.Value);
v.Add($"{entry.Key}({entry.Value.Serial})");
}
// 防止顺序的问题,需要进行排序
v.Sort();
node.Serial = string.Join("", v);
// 计入哈希表
if (!freq.ContainsKey(node.Serial)) {
freq[node.Serial] = 0;
}
freq[node.Serial]++;
}
Construct(root);
var ans = new List<IList<string>>();
// 记录根节点到当前节点的路径
var path = new List<string>();
void Operate(Trie node) {
// 如果序列化表示在哈希表中出现了超过 1 次,就需要删除
if (freq.TryGetValue(node.Serial, out int count) && count > 1) {
return;
}
// 否则将路径加入答案
if (path.Count > 0) {
ans.Add(new List<string>(path));
}
foreach (var entry in node.Children) {
path.Add(entry.Key);
Operate(entry.Value);
path.RemoveAt(path.Count - 1);
}
}
Operate(root);
return ans;
}
}
###Go
type Trie struct {
serial string // 当前节点结构的序列化表示
children map[string]*Trie // 当前节点的子节点
}
func deleteDuplicateFolder(paths [][]string) [][]string {
root := &Trie{children: make(map[string]*Trie)} // 根节点
// 构建字典树
for _, path := range paths {
cur := root
for _, node := range path {
if _, ok := cur.children[node]; !ok {
cur.children[node] = &Trie{children: make(map[string]*Trie)}
}
cur = cur.children[node]
}
}
freq := make(map[string]int) // 哈希表记录每一种序列化表示的出现次数
// 基于深度优先搜索的后序遍历,计算每一个节点结构的序列化表示
var construct func(*Trie)
construct = func(node *Trie) {
if len(node.children) == 0 {
return // 如果是叶节点,无需操作
}
v := make([]string, 0, len(node.children))
for folder, child := range node.children {
construct(child)
v = append(v, folder + "(" + child.serial + ")")
}
sort.Strings(v)
node.serial = strings.Join(v, "")
freq[node.serial]++
}
construct(root)
ans := make([][]string, 0)
path := make([]string, 0)
// 操作字典树,删除重复文件夹
var operate func(*Trie)
operate = func(node *Trie) {
if freq[node.serial] > 1 {
return // 如果序列化表示出现超过1次,需要删除
}
if len(path) > 0 {
tmp := make([]string, len(path))
copy(tmp, path)
ans = append(ans, tmp)
}
for folder, child := range node.children {
path = append(path, folder)
operate(child)
path = path[:len(path) - 1]
}
}
operate(root)
return ans
}
###JavaScript
var deleteDuplicateFolder = function(paths) {
class Trie {
constructor() {
this.serial = ""; // 当前节点结构的序列化表示
this.children = new Map(); // 当前节点的子节点
}
}
const root = new Trie(); // 根节点
// 构建字典树
for (const path of paths) {
let cur = root;
for (const node of path) {
if (!cur.children.has(node)) {
cur.children.set(node, new Trie());
}
cur = cur.children.get(node);
}
}
const freq = new Map(); // 哈希表记录每一种序列化表示的出现次数
// 基于深度优先搜索的后序遍历,计算每一个节点结构的序列化表示
function construct(node) {
if (node.children.size === 0) return; // 如果是叶节点,无需操作
const v = [];
for (const [folder, child] of node.children) {
construct(child);
v.push(`${folder}(${child.serial})`);
}
v.sort();
node.serial = v.join("");
freq.set(node.serial, (freq.get(node.serial) || 0) + 1);
}
construct(root);
const ans = [];
const path = [];
// 操作字典树,删除重复文件夹
function operate(node) {
if ((freq.get(node.serial) || 0) > 1) return; // 如果序列化表示出现超过1次,需要删除
if (path.length > 0) {
ans.push([...path]);
}
for (const [folder, child] of node.children) {
path.push(folder);
operate(child);
path.pop();
}
}
operate(root);
return ans;
}
###TypeScript
function deleteDuplicateFolder(paths: string[][]): string[][] {
class Trie {
serial: string = ""; // 当前节点结构的序列化表示
children: Map<string, Trie> = new Map(); // 当前节点的子节点
}
const root = new Trie(); // 根节点
// 构建字典树
for (const path of paths) {
let cur = root;
for (const node of path) {
if (!cur.children.has(node)) {
cur.children.set(node, new Trie());
}
cur = cur.children.get(node)!;
}
}
const freq = new Map<string, number>(); // 哈希表记录每一种序列化表示的出现次数
// 基于深度优先搜索的后序遍历,计算每一个节点结构的序列化表示
function construct(node: Trie) {
if (node.children.size === 0) return; // 如果是叶节点,无需操作
const v: string[] = [];
for (const [folder, child] of node.children) {
construct(child);
v.push(`${folder}(${child.serial})`);
}
v.sort();
node.serial = v.join("");
freq.set(node.serial, (freq.get(node.serial) || 0) + 1);
}
construct(root);
const ans: string[][] = [];
const path: string[] = [];
// 操作字典树,删除重复文件夹
function operate(node: Trie) {
if ((freq.get(node.serial) || 0) > 1) return; // 如果序列化表示出现超过1次,需要删除
if (path.length > 0) {
ans.push([...path]);
}
for (const [folder, child] of node.children) {
path.push(folder);
operate(child);
path.pop();
}
}
operate(root);
return ans;
}
###Rust
use std::collections::HashMap;
#[derive(Default)]
struct Trie {
serial: String, // 当前节点结构的序列化表示
children: HashMap<String, Trie>, // 当前节点的子节点
}
impl Solution {
pub fn delete_duplicate_folder(paths: Vec<Vec<String>>) -> Vec<Vec<String>> {
let mut root = Trie::default(); // 根节点
// 构建字典树
for path in paths {
let mut cur = &mut root;
for node in path {
cur = cur.children.entry(node.clone()).or_default();
}
}
let mut freq = HashMap::new(); // 哈希表记录每一种序列化表示的出现次数
// 基于深度优先搜索的后序遍历,计算每一个节点结构的序列化表示
fn construct(node: &mut Trie, freq: &mut HashMap<String, usize>) {
if node.children.is_empty() {
return; // 如果是叶节点,无需操作
}
let mut v = Vec::new();
for (folder, child) in node.children.iter_mut() {
construct(child, freq);
v.push(format!("{}({})", folder, child.serial));
}
v.sort();
node.serial = v.join("");
*freq.entry(node.serial.clone()).or_default() += 1;
}
construct(&mut root, &mut freq);
let mut ans = Vec::new();
let mut path = Vec::new();
// 操作字典树,删除重复文件夹
fn operate(node: &Trie, freq: &HashMap<String, usize>, path: &mut Vec<String>, ans: &mut Vec<Vec<String>>) {
if freq.get(&node.serial).unwrap_or(&0) > &1 {
return; // 如果序列化表示出现超过1次,需要删除
}
if !path.is_empty() {
ans.push(path.clone());
}
for (folder, child) in &node.children {
path.push(folder.clone());
operate(child, freq, path, ans);
path.pop();
}
}
operate(&root, &freq, &mut path, &mut ans);
ans
}
}
复杂度分析
这里我们只考虑计算所有节点结构的序列化表示需要的时间,以及哈希映射需要使用的空间。对于其它的项(无论是时间项还是空间项),它们在渐近意义下一定都小于计算以及存储序列化表示的部分,因此可以忽略。
在最坏情况下,节点结构的序列化表示的字符串两两不同,那么需要的时间和空间级别均为「所有节点结构的序列化表示的字符串的长度之和」。如何求出这个长度之和的上界呢?
这里我们需要用到一个很重要的结论:
设 $T$ 为无权多叉树。对于 $T$ 中的节点 $x$,记 $\textit{dist}[x]$ 为从根节点到 $x$ 经过的节点个数,$\textit{size}[x]$ 为以 $x$ 为根的子树的大小,那么有:
$$
\sum_{x \in T} \textit{dist}[x] = \sum_{x \in T} \textit{size}[x]
$$
证明也较为直观。对于任意的节点 $x'$,在右侧的 $\sum_{x \in T} \textit{size}[x]$ 中,$x'$ 被包含在 $\textit{size}[x]$ 中的次数就等于 $x'$ 的祖先节点的数目(也包括 $x'$ 本身),其等于根节点到 $x'$ 的经过的节点个数,因此得证。
回到本题,$\textit{path}$ 中给出了根节点到所有节点的路径,其中最多包含 $2\times 10^5$ 个字符,那么 $\sum_{x \in T} \textit{dist}[x]$ 不超过 $2\times 10^5$,$\sum_{x \in T} \textit{size}[x]$ 同样也不超过 $2\times 10^5$。
对于任意的节点 $x$,$x$ 结构的序列化表示的字符串长度包含两部分,第一部分为其中所有子文件夹名的长度之和,其不超过 $10 \cdot \textit{size}[x]$,第二部分为额外添加的用来区分的括号,由于一个子文件夹会恰好被添加一对括号,因此其不超过 $2 \cdot \textit{size}[x]$。这样一来,「所有节点结构的序列化表示的字符串的长度之和」的上界为:
$$
12 \cdot \sum_{x \in T} \textit{size}[x] = 2.4 \times 10^6
$$
即空间的数量级为 $10^6$。而对于时间,即使算上排序的额外 $\log$ 的时间复杂度,也在 $10^7$ 的数量级,可以在规定的时间内通过本题。并且需要指出的是,在上述估算上界的过程中,我们作出的许多假设是非常极端的,因此实际上该方法的运行时间很快。
 {:width=300}
{:width=300}

