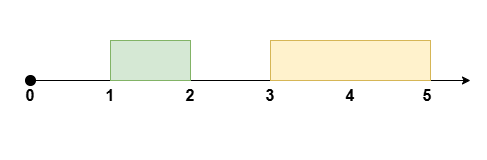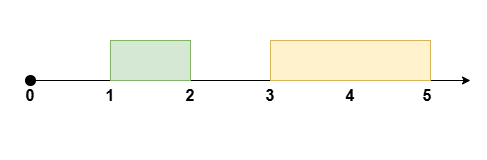方法一:分析本质不同的站位情况 + 记忆化搜索
前言
本题思维难度较大。其中的有些技巧可能在其它的题目中很少出现。
读者在第一次阅读本题解时,可以多去思考「怎么做」,而尽量不要去思考「为什么要这么做」。
思路与算法
我们可以用 $F(n, f, s)$ 表示还剩余 $n$ 个人,并且两名最佳运动员分别是一排中从左往右数的第 $f$ 和 $s$ 名运动员时,他们比拼的最早回合数。
同理,我们用 $G(n, f, s)$ 表示他们比拼的最晚回合数。
那么如何进行状态转移呢?
只考虑本质不同的站位情况
如果我们单纯地用 $F(n, f, s)$ 来进行状态转移,会使得设计出的算法和编写出的代码都相当复杂。例如我们需要考虑 $f$ 是在左侧(即从前往后数)、中间(即轮空)还是右侧(即从后往前数),对于 $s$ 也需要考虑那么多情况,这样状态转移方程就相当麻烦。
我们可以考虑分析出本质不同的站位情况,得到下面的表格:
|
$s$ 在左侧 |
$s$ 在中间 |
$s$ 在右侧 |
| $f$ 在左侧 |
保持不变 |
保持不变 |
保持不变 |
| $f$ 在中间 |
等价于「$f$ 在左侧,$s$ 在中间」 |
不存在这种情况 |
等价于「$f$ 在左侧,$s$ 在中间」 |
| $f$ 在右侧 |
等价于「$f$ 在左侧,$s$ 在右侧」 |
等价于「$f$ 在左侧,$s$ 在中间」 |
等价于「$f$ 在左侧,$s$ 在左侧」 |
其正确性在于:
-
$F(n, f, s) = F(n, s, f)$ 恒成立。即我们交换两名最佳运动员的位置,结果不会发生变化;
-
$F(n, f, s) = F(n, n+1-s, n+1-f)$ 恒成立。因为我们会让从前往后数的第 $i$ 运动员与从后往前数的第 $i$ 名运动员进行比拼,那么我们将所有的运动员看成一个整体,整体翻转一下,结果同样不会发生变化。
我们使用这两条变换规则,就可以保证在 $F(n, f, s)$ 中,$f$ 一定小于 $s$,那么 $f$ 一定在左侧,而 $s$ 可以在左侧、中间或者右侧。这样我们就将原本的 $8$ 种情况减少到了 $3$ 种情况。
对于 $G(n, f, s)$,其做法是完全相同的。
状态转移方程的设计
既然我们知道了 $f$ 一定在左侧,那么我们就可以根据 $s$ 在左侧、中间还是右侧,分别设计状态转移方程了。

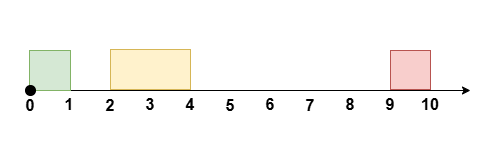
如果 $s$ 在左侧,如上图所示:
-
$f$ 左侧有 $f-1$ 名运动员,它们会与右侧对应的运动员进行比拼,因此剩下 $[0, f-1]$ 名运动员;
-
$f$ 与 $s$ 中间有 $s-f-1$ 名运动员,它们会与右侧对应的运动员进行比拼,因此剩下 $[0, s-f-1]$ 名运动员。
如果 $f-1$ 名运动员中剩下了 $i$ 名,而 $s-f-1$ 名运动员中剩下了 $j$ 名,那么在下一回合中,两名最佳运动员分别位于位置 $i+1$ 和位置 $i+j+2$,而剩余的运动员总数为 $\lfloor \dfrac{n+1}{2} \rfloor$,其中 $\lfloor x \rfloor$ 表示对 $x$ 向下取整。因此我们可以得到状态转移方程:
$$
F(n, f, s) = \left( \min_{i\in [0,f-1], j \in [0, s-f-1]} F(\lfloor \frac{n+1}{2} \rfloor, i + 1, i + j + 2) \right) + 1
$$

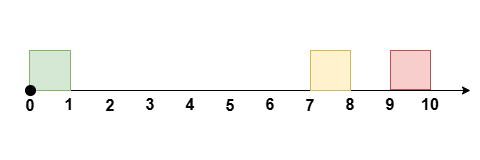
如果 $s$ 在中间,如上图所示,我们可以发现状态转移方程与 $s$ 在左侧的情况是完全相同的。
如果 $s$ 在右侧,那么情况会较为麻烦,会有三种情况:
-
最简单的情况就是 $f$ 和 $s$ 恰好比拼,即 $f+s=n+1$,那么 $F(n, f, s)=1$;
-
此外,设这一回合与 $s$ 比拼的是 $s'=n+1-s$,那么 $f < s'$ 是一种情况,$f > s'$ 是另一种情况。

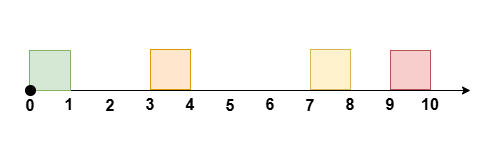
然而我们可以知道,根据类似上一节「本质不同的站位情况」的分析,我们将 $f$ 变为 $n+1-s$,$s$ 变为 $n+1-f$,这样 $f$ 仍然小于 $s$,并且 $f$ 也小于 $s'$ 了。因此我们只需要考虑 $f < s'$ 的情况,如上图所示:
-
$f$ 左侧有 $f-1$ 名运动员,它们会与右侧对应的运动员进行比拼,因此剩下 $[0, f-1]$ 名运动员;
-
$f$ 与 $s'$ 中间有 $s'-f-1$ 名运动员,它们会与右侧对应的运动员进行比拼,因此剩下 $[0, s'-f-1]$ 名运动员;
-
$s'$ 一定会输给 $s$;
-
$s'$ 与 $s$ 中间有 $n - 2s'$ 名运动员。如果 $n-2s'$ 是偶数,那么他们两两之间比拼,剩下 $\dfrac{n-2s'}{2}$ 名运动员;如果 $n-2s'$ 是奇数,那么其中一人轮空,剩余两两之间比拼,剩下 $\dfrac{n-2s'+1}{2}$ 名运动员。因此,无论 $n-2s'$ 是奇数还是偶数,$s'$ 与 $s$ 中间一定会有 $\lfloor \dfrac{n-2s'+1}{2} \rfloor$ 名运动员。
如果 $f-1$ 名运动员中剩下了 $i$ 名,而 $s'-f-1$ 名运动员中剩下了 $j$ 名,那么在下一回合中,两名最佳运动员分别位于位置 $i+1$ 和位置 $i+j+\lfloor \dfrac{n-2s'+1}{2} \rfloor+2$。因此我们可以得到状态转移方程:
$$
F(n, f, s) = \left( \min_{i\in [0,f-1], j \in [0, s'-f-1]} F(\lfloor \frac{n+1}{2} \rfloor, i + 1, i+j+\lfloor \dfrac{n-2s'+1}{2} \rfloor+2) \right) + 1
$$
这样我们就得到了所有关于 $F$ 的状态转移方程。而关于 $G$ 的状态转移方程,我们只需要把所有的 $\min$ 改为 $\max$ 即可。
细节
在「本质不同的站位情况」一节中,我们提到了两种变换规则。那么我们具体应当在 $n, f, s$ 满足什么关系(而不是抽象的「左侧」「中间」「右侧」)时使用其中的哪些规则呢?
这里有很多种设计方法,我们介绍一种较为简单的,题解代码中使用的方法:
-
首先我们使用自顶向下的记忆化搜索代替动态规划进行状态转移,这样写更加简洁直观,并且无需考虑状态的求值顺序;
-
记忆化搜索的入口为 $F(n, \textit{firstPlayer}, \textit{secondPlayer})$。我们在开始记忆化搜索之前,先通过变换规则 $F(n, f, s) = F(n, s, f)$ 使得 $\textit{firstPlayer}$ 一定小于 $\textit{secondPlayer}$,这样一来,由于另一条变换规则 $F(n, f, s) = F(n, n+1-s, n+1-f)$ 不会改变 $f$ 与 $s$ 间的大小关系,因此在接下来的记忆化搜索中,$f < s$ 是恒成立的,我们也就无需使用变换规则 $F(n, f, s) = F(n, s, f)$ 了;
-
在之前表格中,我们需要变换的情况有 $5$ 种,分别是:「$f$ 在中间,$s$ 在左侧」「$f$ 在中间,$s$ 在右侧」「$f$ 在右侧,$s$ 在左侧」「$f$ 在右侧,$s$ 在中间」「$f$ 在右侧,$s$ 在右侧」。由于我们已经保证了 $f < s$ 恒成立,因此这 $5$ 种情况中只剩下 $2$ 种是需要处理的,即:「$f$ 在中间,$s$ 在右侧」和「$f$ 在右侧,$s$ 在右侧」。此外,我们在「状态转移方程的设计」一节中还发现了一种需要处理的情况,即「$f$ 在左侧,$s$ 在右侧,并且 $f>s'=n+1-s$」。
那么这 $3$ 种情况是否可以统一呢?对于最后一种情况,我们有 $f+s > n+1$,而「$f$ 在中间,$s$ 在右侧」和「$f$ 在右侧,$s$ 在右侧」也恰好满足 $f+s > n+1$,并且所有不需要变换的情况都不满足 $f+s > n+1$。因此我们只需要在 $f+s > n+1$ 时,使用一次变换规则 $F(n, f, s) = F(n, n+1-s, n+1-f)$ 就行了。
代码
由于 $\texttt{Python}$ 中可以很方便地使用 $\texttt{@cache}$ 进行记忆化搜索,因此在下面 $\texttt{Python}$ 的代码中,我们无需显式地定义 $F$ 和 $G$,函数 $\textit{dp}(n, f, s)$ 返回的二元组即为 $F(n, f, s)$ 和 $G(n, f, s)$。
###C++
class Solution {
private:
int F[30][30][30], G[30][30][30];
public:
pair<int, int> dp(int n, int f, int s) {
if (F[n][f][s]) {
return {F[n][f][s], G[n][f][s]};
}
if (f + s == n + 1) {
return {1, 1};
}
// F(n,f,s)=F(n,n+1-s,n+1-f)
if (f + s > n + 1) {
tie(F[n][f][s], G[n][f][s]) = dp(n, n + 1 - s, n + 1 - f);
return {F[n][f][s], G[n][f][s]};
}
int earlist = INT_MAX, latest = INT_MIN;
int n_half = (n + 1) / 2;
if (s <= n_half) {
// 在左侧或者中间
for (int i = 0; i < f; ++i) {
for (int j = 0; j < s - f; ++j) {
auto [x, y] = dp(n_half, i + 1, i + j + 2);
earlist = min(earlist, x);
latest = max(latest, y);
}
}
}
else {
// s 在右侧
// s'
int s_prime = n + 1 - s;
int mid = (n - 2 * s_prime + 1) / 2;
for (int i = 0; i < f; ++i) {
for (int j = 0; j < s_prime - f; ++j) {
auto [x, y] = dp(n_half, i + 1, i + j + mid + 2);
earlist = min(earlist, x);
latest = max(latest, y);
}
}
}
return {F[n][f][s] = earlist + 1, G[n][f][s] = latest + 1};
}
vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {
memset(F, 0, sizeof(F));
memset(G, 0, sizeof(G));
// F(n,f,s) = F(n,s,f)
if (firstPlayer > secondPlayer) {
swap(firstPlayer, secondPlayer);
}
auto [earlist, latest] = dp(n, firstPlayer, secondPlayer);
return {earlist, latest};
}
};
###Python
class Solution:
def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:
@cache
def dp(n: int, f: int, s: int) -> (int, int):
if f + s == n + 1:
return (1, 1)
# F(n,f,s)=F(n,n+1-s,n+1-f)
if f + s > n + 1:
return dp(n, n + 1 - s, n + 1 - f)
earliest, latest = float("inf"), float("-inf")
n_half = (n + 1) // 2
if s <= n_half:
# s 在左侧或者中间
for i in range(f):
for j in range(s - f):
x, y = dp(n_half, i + 1, i + j + 2)
earliest = min(earliest, x)
latest = max(latest, y)
else:
# s 在右侧
# s'
s_prime = n + 1 - s
mid = (n - 2 * s_prime + 1) // 2
for i in range(f):
for j in range(s_prime - f):
x, y = dp(n_half, i + 1, i + j + mid + 2)
earliest = min(earliest, x)
latest = max(latest, y)
return (earliest + 1, latest + 1)
# F(n,f,s) = F(n,s,f)
if firstPlayer > secondPlayer:
firstPlayer, secondPlayer = secondPlayer, firstPlayer
earliest, latest = dp(n, firstPlayer, secondPlayer)
dp.cache_clear()
return [earliest, latest]
###Java
class Solution {
private int[][][] F = new int[30][30][30];
private int[][][] G = new int[30][30][30];
private int[] dp(int n, int f, int s) {
if (F[n][f][s] != 0) {
return new int[]{F[n][f][s], G[n][f][s]};
}
if (f + s == n + 1) {
return new int[]{1, 1};
}
// F(n,f,s) = F(n, n + 1 - s, n + 1 - f)
if (f + s > n + 1) {
int[] res = dp(n, n + 1 - s, n + 1 - f);
F[n][f][s] = res[0];
G[n][f][s] = res[1];
return new int[]{F[n][f][s], G[n][f][s]};
}
int earlist = Integer.MAX_VALUE, latest = Integer.MIN_VALUE;
int n_half = (n + 1) / 2;
if (s <= n_half) {
// 在左侧或者中间
for (int i = 0; i < f; ++i) {
for (int j = 0; j < s - f; ++j) {
int[] res = dp(n_half, i + 1, i + j + 2);
earlist = Math.min(earlist, res[0]);
latest = Math.max(latest, res[1]);
}
}
} else {
// s 在右侧
int s_prime = n + 1 - s;
int mid = (n - 2 * s_prime + 1) / 2;
for (int i = 0; i < f; ++i) {
for (int j = 0; j < s_prime - f; ++j) {
int[] res = dp(n_half, i + 1, i + j + mid + 2);
earlist = Math.min(earlist, res[0]);
latest = Math.max(latest, res[1]);
}
}
}
F[n][f][s] = earlist + 1;
G[n][f][s] = latest + 1;
return new int[]{F[n][f][s], G[n][f][s]};
}
public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {
// F(n,f,s) = F(n,s,f)
if (firstPlayer > secondPlayer) {
int temp = firstPlayer;
firstPlayer = secondPlayer;
secondPlayer = temp;
}
int[] res = dp(n, firstPlayer, secondPlayer);
return new int[]{res[0], res[1]};
}
}
###C#
public class Solution {
private int[,,] F = new int[30, 30, 30];
private int[,,] G = new int[30, 30, 30];
private int[] Dp(int n, int f, int s) {
if (F[n, f, s] != 0) {
return new int[]{F[n, f, s], G[n, f, s]};
}
if (f + s == n + 1) {
return new int[]{1, 1};
}
// F(n,f,s) = F(n,n+1-s,n+1-f)
if (f + s > n + 1) {
int[] res = Dp(n, n + 1 - s, n + 1 - f);
F[n, f, s] = res[0];
G[n, f, s] = res[1];
return new int[]{F[n, f, s], G[n, f, s]};
}
int earlist = int.MaxValue, latest = int.MinValue;
int n_half = (n + 1) / 2;
if (s <= n_half) {
// 在左侧或者中间
for (int i = 0; i < f; ++i) {
for (int j = 0; j < s - f; ++j) {
int[] res = Dp(n_half, i + 1, i + j + 2);
earlist = Math.Min(earlist, res[0]);
latest = Math.Max(latest, res[1]);
}
}
} else {
// s 在右侧
int s_prime = n + 1 - s;
int mid = (n - 2 * s_prime + 1) / 2;
for (int i = 0; i < f; ++i) {
for (int j = 0; j < s_prime - f; ++j) {
int[] res = Dp(n_half, i + 1, i + j + mid + 2);
earlist = Math.Min(earlist, res[0]);
latest = Math.Max(latest, res[1]);
}
}
}
F[n, f, s] = earlist + 1;
G[n, f, s] = latest + 1;
return new int[]{F[n, f, s], G[n, f, s]};
}
public int[] EarliestAndLatest(int n, int firstPlayer, int secondPlayer) {
// F(n,f,s) = F(n,s,f)
if (firstPlayer > secondPlayer) {
int temp = firstPlayer;
firstPlayer = secondPlayer;
secondPlayer = temp;
}
int[] res = Dp(n, firstPlayer, secondPlayer);
return new int[]{res[0], res[1]};
}
}
###Go
func earliestAndLatest(n int, firstPlayer int, secondPlayer int) []int {
const maxN = 30
var F [maxN][maxN][maxN]int
var G [maxN][maxN][maxN]int
if firstPlayer > secondPlayer {
firstPlayer, secondPlayer = secondPlayer, firstPlayer
}
var dp func(n, f, s int) (int, int)
dp = func(n, f, s int) (int, int) {
if F[n][f][s] != 0 {
return F[n][f][s], G[n][f][s]
}
if f + s == n + 1 {
return 1, 1
}
// F(n,f,s) = F(n,n+1-s,n+1-f)
if f + s > n + 1 {
x, y := dp(n, n + 1 - s, n + 1 - f)
F[n][f][s] = x
G[n][f][s] = y
return x, y
}
earlist := math.MaxInt32
latest := math.MinInt32
n_half := (n + 1) / 2
if s <= n_half {
// 在左侧或者中间
for i := 0; i < f; i++ {
for j := 0; j < s - f; j++ {
x, y := dp(n_half, i + 1, i + j + 2)
earlist = min(earlist, x)
latest = max(latest, y)
}
}
} else {
// s 在右侧
s_prime := n + 1 - s
mid := (n - 2 * s_prime + 1) / 2
for i := 0; i < f; i++ {
for j := 0; j < s_prime-f; j++ {
x, y := dp(n_half, i + 1, i + j + mid + 2)
earlist = min(earlist, x)
latest = max(latest, y)
}
}
}
F[n][f][s] = earlist + 1
G[n][f][s] = latest + 1
return F[n][f][s], G[n][f][s]
}
earlist, latest := dp(n, firstPlayer, secondPlayer)
return []int{earlist, latest}
}
###C
int F[30][30][30] = {0};
int G[30][30][30] = {0};
void dp(int n, int f, int s, int* earlist, int* latest) {
if (F[n][f][s]) {
*earlist = F[n][f][s];
*latest = G[n][f][s];
return;
}
if (f + s == n + 1) {
*earlist = 1;
*latest = 1;
return;
}
// F(n,f,s) = F(n,n+1-s,n+1-f)
if (f + s > n + 1) {
int x, y;
dp(n, n + 1 - s, n + 1 - f, &x, &y);
F[n][f][s] = x;
G[n][f][s] = y;
*earlist = x;
*latest = y;
return;
}
int min_earlist = INT_MAX;
int max_latest = INT_MIN;
int n_half = (n + 1) / 2;
if (s <= n_half) {
// 在左侧或者中间
for (int i = 0; i < f; ++i) {
for (int j = 0; j < s - f; ++j) {
int x, y;
dp(n_half, i + 1, i + j + 2, &x, &y);
if (x < min_earlist) {
min_earlist = x;
}
if (y > max_latest) {
max_latest = y;
}
}
}
} else {
// s 在右侧
int s_prime = n + 1 - s;
int mid = (n - 2 * s_prime + 1) / 2;
for (int i = 0; i < f; ++i) {
for (int j = 0; j < s_prime - f; ++j) {
int x, y;
dp(n_half, i + 1, i + j + mid + 2, &x, &y);
if (x < min_earlist) {
min_earlist = x;
}
if (y > max_latest) {
max_latest = y;
}
}
}
}
F[n][f][s] = min_earlist + 1;
G[n][f][s] = max_latest + 1;
*earlist = F[n][f][s];
*latest = G[n][f][s];
}
int* earliestAndLatest(int n, int firstPlayer, int secondPlayer, int* returnSize) {
*returnSize = 2;
int* result = (int*)malloc(2 * sizeof(int));
// F(n,f,s) = F(n,s,f)
if (firstPlayer > secondPlayer) {
int temp = firstPlayer;
firstPlayer = secondPlayer;
secondPlayer = temp;
}
int earlist, latest;
dp(n, firstPlayer, secondPlayer, &earlist, &latest);
result[0] = earlist;
result[1] = latest;
return result;
}
###JavaScript
var earliestAndLatest = function(n, firstPlayer, secondPlayer) {
F = Array.from({ length: 30 }, () =>
Array.from({ length: 30 }, () =>
Array(30).fill(0)));
G = Array.from({ length: 30 }, () =>
Array.from({ length: 30 }, () =>
Array(30).fill(0)));
const dp = (n, f, s) => {
if (this.F[n][f][s]) {
return [F[n][f][s], G[n][f][s]];
}
if (f + s === n + 1) {
return [1, 1];
}
// F(n,f,s)=F(n,n+1-s,n+1-f)
if (f + s > n + 1) {
const [x, y] = dp(n, n + 1 - s, n + 1 - f);
F[n][f][s] = x;
G[n][f][s] = y;
return [x, y];
}
let earlist = Infinity;
let latest = -Infinity;
const n_half = Math.floor((n + 1) / 2);
if (s <= n_half) {
// 在左侧或者中间
for (let i = 0; i < f; i++) {
for (let j = 0; j < s - f; j++) {
const [x, y] = dp(n_half, i + 1, i + j + 2);
earlist = Math.min(earlist, x);
latest = Math.max(latest, y);
}
}
} else {
// s 在右侧
const s_prime = n + 1 - s;
const mid = Math.floor((n - 2 * s_prime + 1) / 2);
for (let i = 0; i < f; i++) {
for (let j = 0; j < s_prime - f; j++) {
const [x, y] = dp(n_half, i + 1, i + j + mid + 2);
earlist = Math.min(earlist, x);
latest = Math.max(latest, y);
}
}
}
F[n][f][s] = earlist + 1;
G[n][f][s] = latest + 1;
return [F[n][f][s], G[n][f][s]];
};
// F(n,f,s) = F(n,s,f)
if (firstPlayer > secondPlayer) {
[firstPlayer, secondPlayer] = [secondPlayer, firstPlayer];
}
const [earlist, latest] = dp(n, firstPlayer, secondPlayer);
return [earlist, latest];
};
###TypeScript
function earliestAndLatest(n: number, firstPlayer: number, secondPlayer: number): number[] {
const F = Array.from({ length: 30 }, () =>
Array.from({ length: 30 }, () =>
Array(30).fill(0)));
const G = Array.from({ length: 30 }, () =>
Array.from({ length: 30 }, () =>
Array(30).fill(0)));
function dp(n: number, f: number, s: number): [number, number] {
if (F[n][f][s]) {
return [F[n][f][s], G[n][f][s]];
}
if (f + s === n + 1) {
return [1, 1];
}
// F(n,f,s)=F(n,n+1-s,n+1-f)
if (f + s > n + 1) {
const [x, y] = dp(n, n + 1 - s, n + 1 - f);
F[n][f][s] = x;
G[n][f][s] = y;
return [x, y];
}
let earlist = Infinity;
let latest = -Infinity;
const n_half = Math.floor((n + 1) / 2);
if (s <= n_half) {
// 在左侧或者中间
for (let i = 0; i < f; i++) {
for (let j = 0; j < s - f; j++) {
const [x, y] = dp(n_half, i + 1, i + j + 2);
earlist = Math.min(earlist, x);
latest = Math.max(latest, y);
}
}
} else {
// s 在右侧
const s_prime = n + 1 - s;
const mid = Math.floor((n - 2 * s_prime + 1) / 2);
for (let i = 0; i < f; i++) {
for (let j = 0; j < s_prime - f; j++) {
const [x, y] = dp(n_half, i + 1, i + j + mid + 2);
earlist = Math.min(earlist, x);
latest = Math.max(latest, y);
}
}
}
F[n][f][s] = earlist + 1;
G[n][f][s] = latest + 1;
return [F[n][f][s], G[n][f][s]];
};
// F(n,f,s) = F(n,s,f)
if (firstPlayer > secondPlayer) {
[firstPlayer, secondPlayer] = [secondPlayer, firstPlayer];
}
const [earlist, latest] = dp(n, firstPlayer, secondPlayer);
return [earlist, latest];
};
###Rust
use std::cmp::{min, max};
impl Solution {
pub fn earliest_and_latest(n: i32, first_player: i32, second_player: i32) -> Vec<i32> {
const MAX_N: usize = 30;
let mut f = [[[0; MAX_N]; MAX_N]; MAX_N];
let mut g = [[[0; MAX_N]; MAX_N]; MAX_N];
let mut first = first_player as usize;
let mut second = second_player as usize;
if first > second {
std::mem::swap(&mut first, &mut second);
}
let (earliest, latest) = Self::dp(n as usize, first, second, &mut f, &mut g);
vec![earliest, latest]
}
fn dp(n: usize, first: usize, second: usize, f: &mut [[[i32; 30]; 30]; 30], g: &mut [[[i32; 30]; 30]; 30]) -> (i32, i32) {
if f[n][first][second] != 0 {
return (f[n][first][second], g[n][first][second]);
}
if first + second == n + 1 {
return (1, 1);
}
// 对称情况处理
if first + second > n + 1 {
let (x, y) = Self::dp(n, n + 1 - second, n + 1 - first, f, g);
f[n][first][second] = x;
g[n][first][second] = y;
return (x, y);
}
let mut earliest = i32::MAX;
let mut latest = i32::MIN;
let n_half = (n + 1) / 2;
if second <= n_half {
// 都在左侧或中间
for i in 0..first {
for j in 0..(second - first) {
let (x, y) = Self::dp(n_half, i + 1, i + j + 2, f, g);
earliest = min(earliest, x);
latest = max(latest, y);
}
}
} else {
// second在右侧
let s_prime = n + 1 - second;
let mid = (n - 2 * s_prime + 1) / 2;
for i in 0..first {
for j in 0..(s_prime - first) {
let (x, y) = Self::dp(n_half, i + 1, i + j + mid + 2, f, g);
earliest = min(earliest, x);
latest = max(latest, y);
}
}
}
f[n][first][second] = earliest + 1;
g[n][first][second] = latest + 1;
(f[n][first][second], g[n][first][second])
}
}
复杂度分析
-
时间复杂度:$O(n^4 \log n)$。在状态 $F(n, f, s)$ 中($G(n, f, s)$ 同理),每一维的范围都是 $O(n)$,而每一个状态需要 $O(n^2)$ 的时间枚举所有可以转移而来的状态,因此整个算法的时间复杂度为 $O(n^5)$。
然而我们可以发现,$F(n, f, s)$ 中的 $n$ 的取值个数是有限的,在记忆化搜索的过程中,$n$ 会变成 $\lfloor \dfrac{n+1}{2} \rfloor$ 后继续向下递归,因此 $n$ 的取值个数只有 $O(\log n)$ 种,即总时间复杂度为 $O(n^4 \log n)$。
-
空间复杂度:$O(n^2 \log n)$ 或 $O(n^3)$,即为存储所有状态需要的空间。在 $\texttt{C++}$ 代码中,我们使用数组存储所有状态,即使 $n$ 的取值个数只有 $O(\log n)$ 种,我们还是需要对第一维开辟 $O(n)$ 的空间。而在 $\texttt{Python}$ 代码中,$\texttt{@cache}$ 使用元组 $\texttt{tuple}$ 作为字典 $\texttt{dict}$ 的键来存储所有状态的值,状态的数量为 $O(n^2 \log n)$,那么使用的空间也为 $O(n^2 \log n)$。
此外,由于力扣平台上对于运行时间的计算是取所有测试数据的运行时间总和,所有的测试数据会在一次运行中全部测试完成,而本题中记忆化存储的结果在不同的测试数据之间是可以共享的。因此,代码中清空记忆化结果的命令(例如 $\texttt{C++}$ 中的 $\texttt{memset}$ 或者 $\texttt{Python}$ 中的 $\texttt{cache_clear}$)是可以省略的。



 {:width=550}
{:width=550} {:width=550}
{:width=550} {:width=700}
{:width=700}