分析
如果 $\textit{seq} * k$ 是 $s$ 的子序列,必须满足:
- $\textit{seq}$ 中的每个字母在 $s$ 中至少出现 $k$ 次。
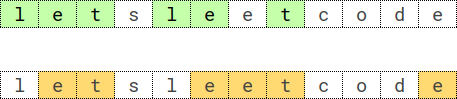
示例 1 的 $s=\texttt{letsleetcode}$,$k=2$,其中 $\texttt{s},\texttt{c},\texttt{o},\texttt{d}$ 这些只出现一次的字母,一定不在 $\textit{seq}$ 中(因为 $\textit{seq}$ 要重复 $k=2$ 次,$1$ 个字母无法重复 $2$ 次)。只有 $\texttt{l},\texttt{e},\texttt{t}$ 这些至少出现 $k$ 次的字母,才可能在 $\textit{seq}$ 中。
分析到这里,题目的这个奇怪的数据范围 $n < 8k$ 就有用了。
设有 $x$ 个字母至少出现 $k$ 次,那么
$$
kx\le n
$$
即
$$
x \le \dfrac{n}{k} < 8
$$
所以至多有 $7$ 个字母至少出现 $k$ 次。
枚举排列
枚举从 $7$ 个字母中选出 $i=1,2,3,4,5,6,7$ 个字母的排列,枚举次数为
$$
A_7^1 + A_7^2 + A_7^3 + A_7^4 + A_7^5 + A_7^6 + A_7^7 = 13699
$$
这不多,在时间范围内可以接受。
在示例 1 中,至少出现 $k=2$ 次的字母有 $\texttt{l},\texttt{e},\texttt{t}$。其中字母 $\texttt{e}$ 出现了 $4$ 次,这意味着 $\textit{seq}$ 中可以有 $\left\lfloor\dfrac{4}{k}\right\rfloor=2$ 个 $\texttt{e}$。所以我们枚举的是 $a=[\texttt{l},\texttt{e},\texttt{e},\texttt{t}]$ 的 47. 全排列 II,我的题解。注意排列中有重复元素。
判断子序列
设当前枚举的排列为 $\textit{seq}$,我们需要判断 $\textit{seq} * k$ 是否为 $s$ 的子序列。
做法见 392. 判断子序列,我的题解。
优化前
class Solution:
# 392. 判断子序列
# 返回 seq 是否为 s 的子序列
def isSubsequence(self, seq: str, s: str) -> bool:
it = iter(s)
return all(c in it for c in seq) # in 会消耗迭代器
def longestSubsequenceRepeatedK(self, s: str, k: int) -> str:
cnt = Counter(s)
a = [ch for ch, freq in cnt.items() for _ in range(freq // k)]
a.sort(reverse=True)
for i in range(len(a), 0, -1):
for perm in permutations(a, i): # a 的长为 i 的排列
seq = ''.join(perm)
if self.isSubsequence(seq * k, s): # seq*k 是 s 的子序列
return seq
return ''
class Solution {
private char[] ans;
private int ansLen = 0;
public String longestSubsequenceRepeatedK(String S, int k) {
char[] s = S.toCharArray();
int[] cnt = new int[26];
for (char c : s) {
cnt[c - 'a']++;
}
StringBuilder tmp = new StringBuilder();
// 倒序,这样我们可以优先枚举字典序大的排列
for (int i = 25; i >= 0; i--) {
String c = String.valueOf((char) ('a' + i));
tmp.append(c.repeat(cnt[i] / k));
}
char[] a = tmp.toString().toCharArray();
ans = new char[a.length];
permute(a, k, s);
return new String(ans, 0, ansLen);
}
// 47. 全排列 II
// 枚举从 nums 中选任意个数的所有排列,处理枚举的排列
private void permute(char[] nums, int k, char[] s) {
int n = nums.length;
char[] path = new char[n];
boolean[] onPath = new boolean[n]; // onPath[j] 表示 nums[j] 是否已经填入排列
dfs(0, nums, path, onPath, k, s);
}
private void dfs(int i, char[] nums, char[] path, boolean[] onPath, int k, char[] s) {
// 处理当前排列 path
process(path, i, k, s);
if (i == nums.length) {
return;
}
// 枚举 nums[j] 填入 path[pathLen]
for (int j = 0; j < nums.length; j++) {
// 如果 nums[j] 已填入排列,continue
// 如果 nums[j] 和前一个数 nums[j-1] 相等,且 nums[j-1] 没填入排列,continue
if (onPath[j] || j > 0 && nums[j] == nums[j - 1] && !onPath[j - 1]) {
continue;
}
path[i] = nums[j]; // 填入排列
onPath[j] = true; // nums[j] 已填入排列(注意标记的是下标,不是值)
dfs(i + 1, nums, path, onPath, k, s); // 填排列的下一个数
onPath[j] = false; // 恢复现场
// 注意 path 无需恢复现场,直接覆盖 path[i] 就行
}
}
private void process(char[] seq, int seqLen, int k, char[] s) {
// 先比大小(时间复杂度低),再判断是否为子序列(时间复杂度高)
if (seqLen > ansLen || seqLen == ansLen && compare(seq, ans, ansLen) > 0) {
if (isSubsequence(seq, seqLen, k, s)) {
System.arraycopy(seq, 0, ans, 0, seqLen);
ansLen = seqLen;
}
}
}
// 比较 a 和 b 的字典序大小
private int compare(char[] a, char[] b, int n) {
for (int i = 0; i < n; i++) {
if (a[i] != b[i]) {
return a[i] - b[i];
}
}
return 0;
}
// 392. 判断子序列
// 返回 seq*k 是否为 s 的子序列
private boolean isSubsequence(char[] seq, int n, int k, char[] s) {
int i = 0;
for (char c : s) {
if (seq[i % n] == c) {
i++;
if (i == n * k) { // seq*k 的所有字符匹配完毕
return true; // seq*k 是 s 的子序列
}
}
}
return false;
}
}
class Solution {
// 47. 全排列 II
// 枚举从 nums 中选任意个数的所有排列,用 f 处理枚举的排列
void permuteFunc(const string& nums, auto&& f) {
int n = nums.size();
string path;
vector<int8_t> on_path(n); // on_path[j] 表示 nums[j] 是否已经填入排列
auto dfs = [&](this auto&& dfs) -> void {
f(path);
if (path.size() == n) {
return;
}
// 枚举 nums[j] 填入 path[i]
for (int j = 0; j < n; j++) {
// 如果 nums[j] 已填入排列,continue
// 如果 nums[j] 和前一个数 nums[j-1] 相等,且 nums[j-1] 没填入排列,continue
if (on_path[j] || j > 0 && nums[j] == nums[j - 1] && !on_path[j - 1]) {
continue;
}
path += nums[j]; // 填入排列
on_path[j] = true; // nums[j] 已填入排列(注意标记的是下标,不是值)
dfs(); // 填排列的下一个数
on_path[j] = false; // 恢复现场
path.pop_back(); // 恢复现场
}
};
dfs();
};
// 392. 判断子序列
// 返回 seq*k 是否为 s 的子序列
bool isSubsequence(const string& seq, int k, const string& s) {
int n = seq.size();
int i = 0;
for (char c : s) {
if (seq[i % n] == c) {
i++;
if (i == n * k) { // seq*k 的所有字符匹配完毕
return true; // seq*k 是 s 的子序列
}
}
}
return false;
}
public:
string longestSubsequenceRepeatedK(string s, int k) {
int cnt[26]{};
for (char c : s) {
cnt[c - 'a']++;
}
string a;
for (int i = 25; i >= 0; i--) { // 倒序,这样我们可以优先枚举字典序大的排列
a.insert(a.end(), cnt[i] / k, 'a' + i);
}
string ans;
permuteFunc(a, [&](const string& seq) {
// 先比大小(时间复杂度低),再判断是否为子序列(时间复杂度高)
if (seq.size() > ans.size() || seq.size() == ans.size() && seq > ans) {
if (isSubsequence(seq, k, s)) {
ans = seq;
}
}
});
return ans;
}
};
// 47. 全排列 II
// 枚举从 nums 中选任意个数的所有排列,用 f 处理枚举的排列
func permuteFunc[T comparable](nums []T, f func([]T)) {
n := len(nums)
path := []T{}
onPath := make([]bool, n) // onPath[j] 表示 nums[j] 是否已经填入排列
var dfs func()
dfs = func() {
f(path)
if len(path) == n {
return
}
// 枚举 nums[j] 填入 path[i]
for j, on := range onPath {
// 如果 nums[j] 已填入排列,continue
// 如果 nums[j] 和前一个数 nums[j-1] 相等,且 nums[j-1] 没填入排列,continue
if on || j > 0 && nums[j] == nums[j-1] && !onPath[j-1] {
continue
}
path = append(path, nums[j])
onPath[j] = true // nums[j] 已填入排列(注意标记的是下标,不是值)
dfs() // 填排列的下一个数
onPath[j] = false // 恢复现场
path = path[:len(path)-1] // 恢复现场
}
}
dfs()
}
// 392. 判断子序列
// 返回 seq*k 是否为 s 的子序列
func isSubsequence(seq []byte, k int, s string) bool {
n := len(seq)
i := 0
for _, c := range s {
if seq[i%n] == byte(c) {
i++
if i == n*k { // seq*k 的所有字符匹配完毕
return true // seq*k 是 s 的子序列
}
}
}
return false
}
func longestSubsequenceRepeatedK(s string, k int) string {
cnt := [26]int{}
for _, c := range s {
cnt[c-'a']++
}
a := []byte{}
for i := 25; i >= 0; i-- { // 倒序,这样我们可以优先枚举字典序大的排列
bs := []byte{'a' + byte(i)}
a = append(a, bytes.Repeat(bs, cnt[i]/k)...)
}
ans := []byte{}
permuteFunc(a, func(seq []byte) {
// 先比大小(时间复杂度低),再判断是否为子序列(时间复杂度高)
if len(seq) > len(ans) || len(seq) == len(ans) && bytes.Compare(seq, ans) > 0 {
if isSubsequence(seq, k, s) {
ans = slices.Clone(seq)
}
}
})
return string(ans)
}
优化:子序列自动机
用 392 题的进阶做法(子序列自动机),原理见 我的题解。
class Solution:
def longestSubsequenceRepeatedK(self, s: str, k: int) -> str:
s = [ord(c) - ord('a') for c in s] # 转成 0 到 25,这样下面无需频繁调用 ord
# 392. 判断子序列(进阶做法)
n = len(s)
nxt = [[n] * 26 for _ in range(n + 1)]
for i in range(n - 1, -1, -1):
nxt[i][:] = nxt[i + 1]
nxt[i][s[i]] = i
def isSubsequence(seq: Tuple[int, ...]) -> bool:
i = -1
for _ in range(k):
for c in seq:
i = nxt[i + 1][c]
if i == n: # c 不在 s 中,说明 seq*k 不是 s 的子序列
return False
return True # seq*k 是 s 的子序列
cnt = Counter(s)
a = [ch for ch, freq in cnt.items() for _ in range(freq // k)]
a.sort(reverse=True) # 排序后,下面会按照字典序从大到小枚举排列
for i in range(len(a), 0, -1): # 长度优先
for seq in permutations(a, i): # 枚举 a 的长为 i 的排列
if isSubsequence(seq):
return ''.join(ascii_lowercase[c] for c in seq)
return ''
class Solution {
private char[] ans;
private int ansLen = 0;
public String longestSubsequenceRepeatedK(String S, int k) {
char[] s = S.toCharArray();
// 392. 判断子序列(进阶做法)
int n = s.length;
int[] cnt = new int[26];
int[][] nxt = new int[n + 1][];
nxt[n] = new int[26];
Arrays.fill(nxt[n], n);
for (int i = n - 1; i >= 0; i--) {
int c = s[i] - 'a';
nxt[i] = nxt[i + 1].clone();
nxt[i][c] = i;
cnt[c]++;
}
StringBuilder tmp = new StringBuilder();
// 倒序,这样我们可以优先枚举字典序大的排列
for (int i = 25; i >= 0; i--) {
String c = String.valueOf((char) ('a' + i));
tmp.append(c.repeat(cnt[i] / k));
}
char[] a = tmp.toString().toCharArray();
ans = new char[a.length];
permute(a, k, nxt);
return new String(ans, 0, ansLen);
}
// 47. 全排列 II
// 枚举从 nums 中选任意个数的所有排列,处理枚举的排列
private void permute(char[] nums, int k, int[][] nxt) {
int n = nums.length;
char[] path = new char[n];
boolean[] onPath = new boolean[n]; // onPath[j] 表示 nums[j] 是否已经填入排列
dfs(0, nums, path, onPath, k, nxt);
}
private void dfs(int i, char[] nums, char[] path, boolean[] onPath, int k, int[][] nxt) {
// 处理当前排列 path
process(path, i, k, nxt);
if (i == nums.length) {
return;
}
// 枚举 nums[j] 填入 path[pathLen]
for (int j = 0; j < nums.length; j++) {
// 如果 nums[j] 已填入排列,continue
// 如果 nums[j] 和前一个数 nums[j-1] 相等,且 nums[j-1] 没填入排列,continue
if (onPath[j] || j > 0 && nums[j] == nums[j - 1] && !onPath[j - 1]) {
continue;
}
path[i] = nums[j]; // 填入排列
onPath[j] = true; // nums[j] 已填入排列(注意标记的是下标,不是值)
dfs(i + 1, nums, path, onPath, k, nxt); // 填排列的下一个数
onPath[j] = false; // 恢复现场
// 注意 path 无需恢复现场,直接覆盖 path[i] 就行
}
}
private void process(char[] seq, int seqLen, int k, int[][] nxt) {
// 先比大小(时间复杂度低),再判断是否为子序列(时间复杂度高)
if (seqLen > ansLen || seqLen == ansLen && compare(seq, ans, ansLen) > 0) {
if (isSubsequence(seq, seqLen, k, nxt)) {
System.arraycopy(seq, 0, ans, 0, seqLen);
ansLen = seqLen;
}
}
}
// 比较 a 和 b 的字典序大小
private int compare(char[] a, char[] b, int n) {
for (int i = 0; i < n; i++) {
if (a[i] != b[i]) {
return a[i] - b[i];
}
}
return 0;
}
// 392. 判断子序列
// 返回 seq*k 是否为 s 的子序列
private boolean isSubsequence(char[] seq, int n, int k, int[][] nxt) {
int i = -1;
while (k-- > 0) {
for (int j = 0; j < n; j++) {
char c = seq[j];
i = nxt[i + 1][c - 'a'];
if (i + 1 == nxt.length) { // c 不在 s 中,说明 seq*k 不是 s 的子序列
return false;
}
}
}
return true;
}
}
class Solution {
// 47. 全排列 II
// 枚举从 nums 中选任意个数的所有排列,用 f 处理枚举的排列
void permuteFunc(const string& nums, auto&& f) {
int n = nums.size();
string path;
vector<int8_t> on_path(n); // on_path[j] 表示 nums[j] 是否已经填入排列
auto dfs = [&](this auto&& dfs) -> void {
f(path);
if (path.size() == n) {
return;
}
// 枚举 nums[j] 填入 path[i]
for (int j = 0; j < n; j++) {
// 如果 nums[j] 已填入排列,continue
// 如果 nums[j] 和前一个数 nums[j-1] 相等,且 nums[j-1] 没填入排列,continue
if (on_path[j] || j > 0 && nums[j] == nums[j - 1] && !on_path[j - 1]) {
continue;
}
path += nums[j]; // 填入排列
on_path[j] = true; // nums[j] 已填入排列(注意标记的是下标,不是值)
dfs(); // 填排列的下一个数
on_path[j] = false; // 恢复现场
path.pop_back(); // 恢复现场
}
};
dfs();
};
public:
string longestSubsequenceRepeatedK(string s, int k) {
// 392. 判断子序列(进阶做法)
int n = s.size();
vector<array<int, 26>> nxt(n + 1);
ranges::fill(nxt[n], n);
for (int i = n - 1; i >= 0; i--) {
nxt[i] = nxt[i + 1];
nxt[i][s[i] - 'a'] = i;
}
auto isSubsequence = [&](const string& seq, int k) -> bool {
int i = -1;
while (k--) {
for (char c : seq) {
i = nxt[i + 1][c - 'a'];
if (i == n) { // c 不在 s 中,说明 seq*k 不是 s 的子序列
return false;
}
}
}
return true;
};
int cnt[26]{};
for (char c : s) {
cnt[c - 'a']++;
}
string a;
for (int i = 25; i >= 0; i--) { // 倒序,这样我们可以优先枚举字典序大的排列
a.insert(a.end(), cnt[i] / k, 'a' + i);
}
string ans;
permuteFunc(a, [&](const string& seq) {
// 先比大小(时间复杂度低),再判断是否为子序列(时间复杂度高)
if (seq.size() > ans.size() || seq.size() == ans.size() && seq > ans) {
if (isSubsequence(seq, k)) {
ans = seq;
}
}
});
return ans;
}
};
// 47. 全排列 II
// 枚举从 nums 中选任意个数的所有排列,用 f 处理枚举的排列
func permuteFunc[T comparable](nums []T, f func([]T)) {
n := len(nums)
path := []T{}
onPath := make([]bool, n) // onPath[j] 表示 nums[j] 是否已经填入排列
var dfs func()
dfs = func() {
f(path)
if len(path) == n {
return
}
// 枚举 nums[j] 填入 path[i]
for j, on := range onPath {
// 如果 nums[j] 已填入排列,continue
// 如果 nums[j] 和前一个数 nums[j-1] 相等,且 nums[j-1] 没填入排列,continue
if on || j > 0 && nums[j] == nums[j-1] && !onPath[j-1] {
continue
}
path = append(path, nums[j])
onPath[j] = true // nums[j] 已填入排列(注意标记的是下标,不是值)
dfs() // 填排列的下一个数
onPath[j] = false // 恢复现场
path = path[:len(path)-1]
}
}
dfs()
}
func longestSubsequenceRepeatedK(s string, k int) string {
// 392. 判断子序列(进阶做法)
n := len(s)
nxt := make([][26]int, n+1)
for j := range nxt[n] {
nxt[n][j] = n
}
for i := n - 1; i >= 0; i-- {
nxt[i] = nxt[i+1]
nxt[i][s[i]-'a'] = i
}
isSubsequence := func(seq []byte) bool {
i := -1
for range k {
for _, c := range seq {
i = nxt[i+1][c-'a']
if i == n { // c 不在 s 中,说明 seq*k 不是 s 的子序列
return false
}
}
}
return true
}
cnt := [26]int{}
for _, c := range s {
cnt[c-'a']++
}
a := []byte{}
for i := 25; i >= 0; i-- { // 倒序,这样我们可以优先枚举字典序大的排列
bs := []byte{'a' + byte(i)}
a = append(a, bytes.Repeat(bs, cnt[i]/k)...)
}
ans := []byte{}
permuteFunc(a, func(seq []byte) {
// 先比大小(时间复杂度低),再判断是否为子序列(时间复杂度高)
if len(seq) > len(ans) || len(seq) == len(ans) && bytes.Compare(seq, ans) > 0 {
if isSubsequence(seq) {
ans = slices.Clone(seq)
}
}
})
return string(ans)
}
复杂度分析
- 时间复杂度:$\mathcal{O}((n/k)!\cdot n)$,其中 $n$ 是 $s$ 的长度。注意 $\sum_{i=0}^m A_m^i$ 就是全排列搜索树的节点个数,我在 排列型回溯【基础算法精讲 16】中精确地算出了全排列搜索树的节点个数为 $\left\lfloor e\cdot m!\right\rfloor$,其中 $e=2.718\cdots$ 为自然常数。比如 $m=7$ 时,$\sum_{i=0}^7 A_7^i = 13700 = \left\lfloor e\cdot 7!\right\rfloor$。当 $m=n/k$ 时,遍历这棵搜索树需要 $\mathcal{O}((n/k)!)$ 的时间,每个节点判断子序列需要 $\mathcal{O}(n)$ 的时间。
- 空间复杂度:$\mathcal{O}(n|\Sigma|)$。其中 $|\Sigma|=26$ 是字符集合的大小。
相似题目
- 回溯题单的「§4.5 排列型回溯」。
- 双指针题单的「§4.2 判断子序列」。
- 字符串题单的「九、子序列自动机」。
分类题单
如何科学刷题?
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 二分算法(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流)
- 动态规划(入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、二叉树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA/一般树)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)
我的题解精选(已分类)
欢迎关注 B站@灵茶山艾府
 {:width=400}
{:width=400}