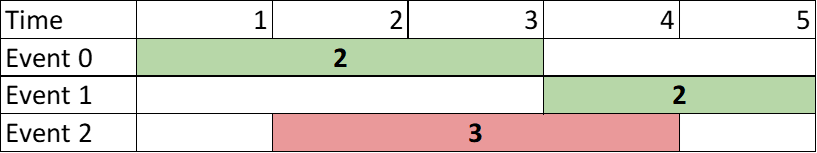方法一:时间戳排序
思路与算法
我们可以将所有活动的左右边界放在一起进行自定义排序。具体地,我们用 $(\textit{ts}, \textit{op}, \textit{val})$ 表示一个「事件」:
-
$\textit{op}$ 表示该事件的类型。如果 $\textit{op} = 0$,说明该事件表示一个活动的开始;如果 $\textit{op} = 1$,说明该事件表示一个活动的结束。
-
$\textit{ts}$ 表示该事件发生的时间,即活动的开始时间或结束时间。
-
$\textit{val}$ 表示该事件的价值,即对应活动的 $\textit{value}$ 值。
我们将所有的时间按照 $\textit{ts}$ 为第一关键字升序排序,这样我们就能按照时间顺序依次处理每一个事件。当 $\textit{ts}$ 相等时,我们按照 $\textit{op}$ 为第二关键字升序排序,这是因为题目中要求了「第一个活动的结束时间不能等于第二个活动的起始时间」,因此当时间相同时,我们先处理开始的事件,再处理结束的事件。
当排序完成后,我们就可以通过对所有的事件进行一次遍历,从而算出最多两个时间不重叠的活动的最大价值:
-
当我们遍历到一个结束事件时,我们用 $\textit{val}$ 来更新 $\textit{bestFirst}$,其中 $\textit{bestFirst}$ 表示当前已经结束的所有活动的最大价值。这样做的意义在于,所有已经结束的事件都可以当作第一个活动。
-
当我们遍历到一个开始事件时,我们将该活动当作第二个活动,由于第一个活动的最大价值为 $\textit{bestFirst}$,因此我们用 $\textit{val} + \textit{bestFirst}$ 更新答案即可。
代码
###C++
struct Event {
// 时间戳
int ts;
// op = 0 表示左边界,op = 1 表示右边界
int op;
int val;
Event(int _ts, int _op, int _val): ts(_ts), op(_op), val(_val) {}
bool operator< (const Event& that) const {
return tie(ts, op) < tie(that.ts, that.op);
}
};
class Solution {
public:
int maxTwoEvents(vector<vector<int>>& events) {
vector<Event> evs;
for (const auto& event: events) {
evs.emplace_back(event[0], 0, event[2]);
evs.emplace_back(event[1], 1, event[2]);
}
sort(evs.begin(), evs.end());
int ans = 0, bestFirst = 0;
for (const auto& [ts, op, val]: evs) {
if (op == 0) {
ans = max(ans, val + bestFirst);
}
else {
bestFirst = max(bestFirst, val);
}
}
return ans;
}
};
###Python
class Event:
def __init__(self, ts: int, op: int, val: int):
self.ts = ts
self.op = op
self.val = val
def __lt__(self, other: "Event") -> bool:
return (self.ts, self.op) < (other.ts, other.op)
class Solution:
def maxTwoEvents(self, events: List[List[int]]) -> int:
evs = list()
for event in events:
evs.append(Event(event[0], 0, event[2]))
evs.append(Event(event[1], 1, event[2]))
evs.sort()
ans = bestFirst = 0
for ev in evs:
if ev.op == 0:
ans = max(ans, ev.val + bestFirst)
else:
bestFirst = max(bestFirst, ev.val)
return ans
###Java
class Solution {
public int maxTwoEvents(int[][] events) {
List<Event> evs = new ArrayList<>();
for (int[] event : events) {
evs.add(new Event(event[0], 0, event[2]));
evs.add(new Event(event[1], 1, event[2]));
}
Collections.sort(evs);
int ans = 0, bestFirst = 0;
for (Event event : evs) {
if (event.op == 0) {
ans = Math.max(ans, event.val + bestFirst);
} else {
bestFirst = Math.max(bestFirst, event.val);
}
}
return ans;
}
class Event implements Comparable<Event> {
int ts;
int op;
int val;
Event(int ts, int op, int val) {
this.ts = ts;
this.op = op;
this.val = val;
}
@Override
public int compareTo(Event other) {
if (this.ts != other.ts) {
return Integer.compare(this.ts, other.ts);
}
return Integer.compare(this.op, other.op);
}
}
}
###C#
public class Solution {
public int MaxTwoEvents(int[][] events) {
List<Event> evs = new List<Event>();
foreach (var eventArr in events) {
evs.Add(new Event(eventArr[0], 0, eventArr[2]));
evs.Add(new Event(eventArr[1], 1, eventArr[2]));
}
evs.Sort();
int ans = 0, bestFirst = 0;
foreach (var ev in evs) {
if (ev.Op == 0) {
ans = Math.Max(ans, ev.Val + bestFirst);
} else {
bestFirst = Math.Max(bestFirst, ev.Val);
}
}
return ans;
}
class Event : IComparable<Event> {
public int Ts { get; set; }
public int Op { get; set; }
public int Val { get; set; }
public Event(int ts, int op, int val) {
Ts = ts;
Op = op;
Val = val;
}
public int CompareTo(Event other) {
if (Ts != other.Ts) {
return Ts.CompareTo(other.Ts);
}
return Op.CompareTo(other.Op);
}
}
}
###Go
func maxTwoEvents(events [][]int) int {
type Event struct {
ts int
op int
val int
}
evs := make([]Event, 0)
for _, event := range events {
evs = append(evs, Event{event[0], 0, event[2]})
evs = append(evs, Event{event[1], 1, event[2]})
}
sort.Slice(evs, func(i, j int) bool {
if evs[i].ts != evs[j].ts {
return evs[i].ts < evs[j].ts
}
return evs[i].op < evs[j].op
})
ans, bestFirst := 0, 0
for _, ev := range evs {
if ev.op == 0 {
if ev.val + bestFirst > ans {
ans = ev.val + bestFirst
}
} else {
if ev.val > bestFirst {
bestFirst = ev.val
}
}
}
return ans
}
###C
typedef struct {
int ts;
int op;
int val;
} Event;
int compareEvents(const void* a, const void* b) {
Event* e1 = (Event*)a;
Event* e2 = (Event*)b;
if (e1->ts != e2->ts) {
return e1->ts - e2->ts;
}
return e1->op - e2->op;
}
int maxTwoEvents(int** events, int eventsSize, int* eventsColSize) {
Event* evs = (Event*)malloc(2 * eventsSize * sizeof(Event));
int idx = 0;
for (int i = 0; i < eventsSize; i++) {
evs[idx++] = (Event){events[i][0], 0, events[i][2]};
evs[idx++] = (Event){events[i][1], 1, events[i][2]};
}
qsort(evs, 2 * eventsSize, sizeof(Event), compareEvents);
int ans = 0, bestFirst = 0;
for (int i = 0; i < 2 * eventsSize; i++) {
if (evs[i].op == 0) {
if (evs[i].val + bestFirst > ans) {
ans = evs[i].val + bestFirst;
}
} else {
if (evs[i].val > bestFirst) {
bestFirst = evs[i].val;
}
}
}
free(evs);
return ans;
}
###JavaScript
var maxTwoEvents = function(events) {
const evs = [];
for (const event of events) {
evs.push({ts: event[0], op: 0, val: event[2]});
evs.push({ts: event[1], op: 1, val: event[2]});
}
evs.sort((a, b) => {
if (a.ts !== b.ts) {
return a.ts - b.ts;
}
return a.op - b.op;
});
let ans = 0, bestFirst = 0;
for (const ev of evs) {
if (ev.op === 0) {
ans = Math.max(ans, ev.val + bestFirst);
} else {
bestFirst = Math.max(bestFirst, ev.val);
}
}
return ans;
};
###TypeScript
function maxTwoEvents(events: number[][]): number {
interface Event {
ts: number;
op: number;
val: number;
}
const evs: Event[] = [];
for (const event of events) {
evs.push({ts: event[0], op: 0, val: event[2]});
evs.push({ts: event[1], op: 1, val: event[2]});
}
evs.sort((a, b) => {
if (a.ts !== b.ts) {
return a.ts - b.ts;
}
return a.op - b.op;
});
let ans = 0, bestFirst = 0;
for (const ev of evs) {
if (ev.op === 0) {
ans = Math.max(ans, ev.val + bestFirst);
} else {
bestFirst = Math.max(bestFirst, ev.val);
}
}
return ans;
}
###Rust
#[derive(Debug)]
struct Event {
ts: i32,
op: i32,
val: i32,
}
impl Solution {
pub fn max_two_events(events: Vec<Vec<i32>>) -> i32 {
let mut evs: Vec<Event> = Vec::new();
for event in events {
evs.push(Event { ts: event[0], op: 0, val: event[2] });
evs.push(Event { ts: event[1], op: 1, val: event[2] });
}
evs.sort_by(|a, b| {
if a.ts != b.ts {
a.ts.cmp(&b.ts)
} else {
a.op.cmp(&b.op)
}
});
let mut ans = 0;
let mut best_first = 0;
for ev in evs {
if ev.op == 0 {
ans = ans.max(ev.val + best_first);
} else {
best_first = best_first.max(ev.val);
}
}
ans
}
}
复杂度分析