引言

背包问题是动态规划中的经典问题，也是 GESP 六级必考的知识点。其原理虽然需要花一些时间，但大多数孩子都能掌握，但是到了具体的题目时，因为背包问题变化较多，就不那么容易写出代码来。

本文将试图把背包问题的各种考法都列举出来，帮助大家巩固练习。

背包问题

背包问题之所以叫这个名字，是因为其背景故事是：往一个容量有限的背包里面，放入一些物品。每个物品有不同的体积大小，所以会占用相应的背包的容量。物品不能被分割，所以要么整个放入背包中，要么不放入。我们需要找出放入背包的价值最大的方案。

举一个简单的例子，背包容量是 10L：

• 物品 1：体积 7 L，价值 8
• 物品 2：体积 5 L，价值 5
• 物品 3：体积 4 L，价值 4

虽然物品 1 的价值最大，价值/体积(即单位体积的价值)也最大，但是因为放入物品 1 之后，剩余的空间 3L 无法再放入别的物品而浪费掉了。就不如不放物品 1，而放入物品 2 和物品 3 带来的总价值大。

由此我们也能看出，背包问题不能用简单的贪心来解决，而需要用动态规划。

解题思路

背包问题的转移方程可以被优化为一维，但为了方便理解，我们先看没有优化的版本。我们定义：

• 每个元素的体积为 a[i]，价值为 v[i]。
• dp[i][j] 表示用前 i 个物品，放入容量为 j 的背包时，所能达到的最大价值

那对于第 i 个物品，如果我们已经知道了前面的结果，那么我们有两种选择：

• 不放入 第 i 个物品，这样 dp[i][j] = dp[i-1][j]
• 放入 第 i 个物品，这样 dp[i][j] = dp[i-1][j-a[i]] + v[i]

而以上就是状态转移方程，我们在上面两种情况下取最优的情况：dp[i][j] = max(dp[i-1][j], dp[i-1][j-a[i]] + v[i]) 。

另外我们需要考虑一下初始化的情况，即 dp[0][1~n] 应该怎么赋值。因为前 0 个物品什么都没选，那么价值肯定都是 0，所以让它们都等于 0 即可。

将以上逻辑写成代码如下：

1
2
3
4
5
6
7

memset(dp, 0, sizeof dp);
for (int i = 1; i <= 3; ++i)
    for (int j = 1; j <= 10; ++j) {
        dp[i][j] = dp[i-1][j];
        if (j-a[i]>=0)
            dp[i][j] = max(dp[i][j], dp[i-1][j-a[i]] + v[i]);
    }

在这段代码中，为了保证 j-a[i] 的值为正，加了一个 if 来检查，保证没有下标越界的代码。如果下标越界，有可能会读取到随机值，也可能读取到非法地址，造成运行异常（Runtime Error）。

我们再用刚刚的例子来做一下表格演示：背包容量是 10L。

• 物品 1：体积 7 L，价值 8
• 物品 2：体积 5 L，价值 5
• 物品 3：体积 4 L，价值 4

经过转移方程的计算，最终，我们可以填出下面这个二维表格，表格中的每一项都计算出来了用前 i 个物品，体积为 j 时的最优化方案。这也是符合动态规划的最优子结构的特征。

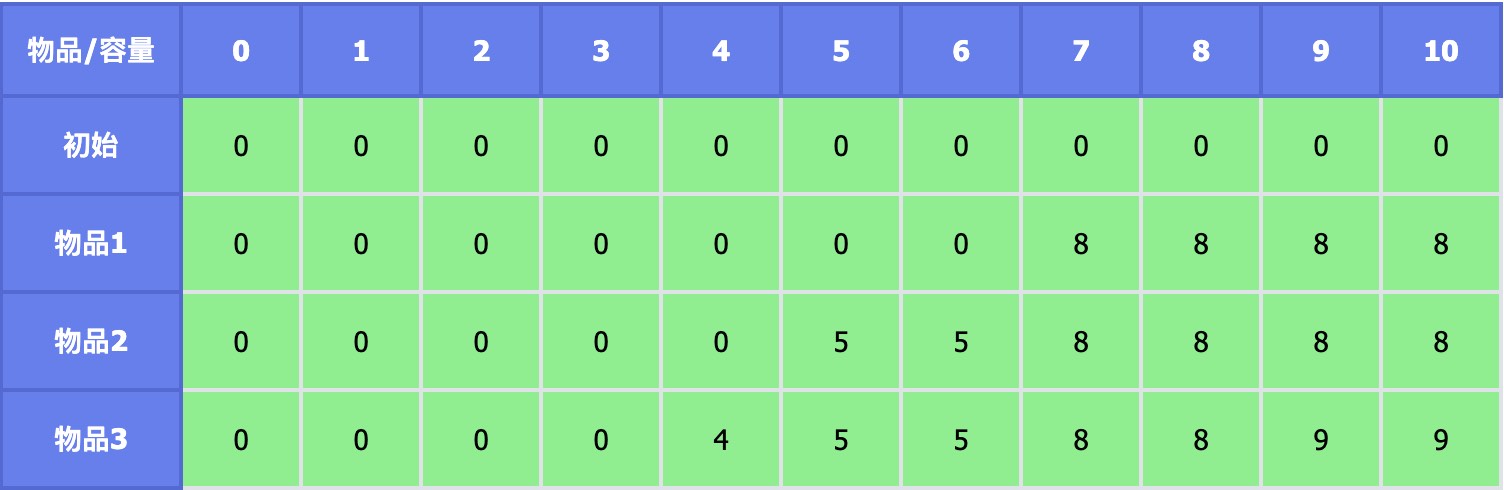
01 背包

所谓的 01 背包，就是指物品的数量只有 1 个，只有选与不选两种方案。刚刚的例子就是一个 01 背包的例子。

我们发现 dp[i][j] 只与两个值相关 dp[i-1][j] 和 dp[i-1][j-a[i]]，这样的二维数组利用的效率很低。所以，我们就想到，能不能把第 i 维省略掉，这样可以节省存储空间（但没有节省运算时间）。

压缩后的代码如下：

1
2
3
4
5

memset(dp, 0, sizeof dp);
for (int i = 1; i <= 3; ++i)
    for (int j = 10; j >= a[i]; --j) {
        dp[j] = max(dp[j], dp[j-a[i]] + v[i]);
    }

我们注意到，j 的循环方式从正序变成了逆序。之所以要这么操作，读者可以用表格的方式，把正着循环的结果填一下就能明白。

如果 j 不是倒着循环，在一轮 j 的循环过程中，dp[j] 的值会在修改后，再一次被访问到，这样就会使得一个物品实际上已经计算了放入的价值，又被重复计算第二次。

完全背包

一个物品被多次重复放入和重复计算价值，其实是我们在完全背包问题中需要的效果。所以，刚刚的代码，如果我们把 j 正序循环，就是完全背包的代码，如下所示：

1
2
3
4
5

memset(dp, 0, sizeof dp);
for (int i = 1; i <= 3; ++i)
    for (int j = a[i]; j <= 10; ++j) {
        dp[j] = max(dp[j], dp[j-a[i]] + v[i]);
    }

但是为了方便理解，我们还是把完全背包的非压维代码也一并看一下：

1
2
3
4
5
6
7
8
9

memset(dp, 0, sizeof dp);
for (int i = 1; i <= 3; ++i)
    for (int j = 1; j <= 10; ++j) {
        dp[i][j] = dp[i-1][j];
        if (j-a[i]>=0) {
            dp[i][j] = max(dp[i][j], dp[i-1][j-a[i]] + v[i]);
            dp[i][j] = max(dp[i][j], dp[i][j-a[i]] + v[i]);
        }
    }

因为 dp[i][j-a[i]] >= dp[i-1][j-a[i]]，所以以上代码可以省略成：

1
2
3
4
5
6
7
8

memset(dp, 0, sizeof dp);
for (int i = 1; i <= 3; ++i)
    for (int j = 1; j <= 10; ++j) {
        dp[i][j] = dp[i-1][j];
        if (j-a[i]>=0) {
            dp[i][j] = max(dp[i][j], dp[i][j-a[i]] + v[i]);
        }
    }

我们可以记住这个写法，因为后面有一些题因为各种情况可能无法压维，就会需要这种写法。

我们还是用刚刚的例子来填写二维表格，背包容量是 10L。物品数量改为无限。

• 物品 1：体积 7 L，价值 8
• 物品 2：体积 5 L，价值 5
• 物品 3：体积 4 L，价值 4

以下是填写出来的值：

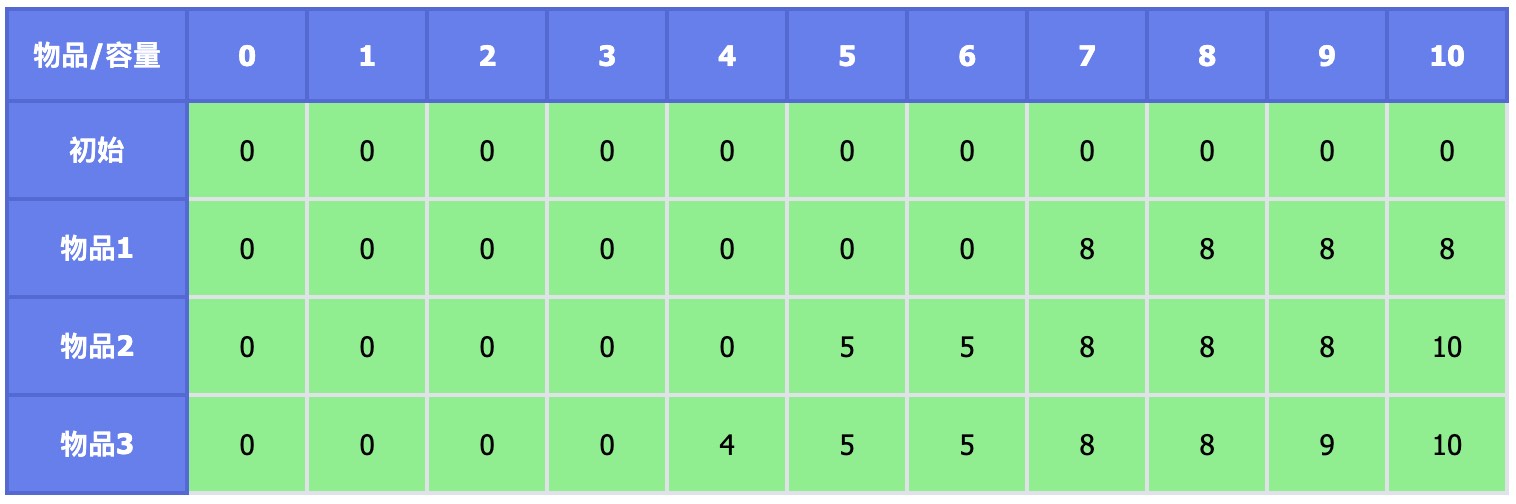
题目变为完全背包后，可以看到最后答案变了，最优方案变成了放入两个物品 2，得到最大价值 10。

学习完以上内容后，可以让学生练习以下两道题：

多重背包

多重背包描述了这样一种场景，一个物品将同时受两个限制条件的制约，例如：一个背包，即有体积限制，又有重量限制，让你往里放物品，求最大化物品价值的放法。

P1794 装备运输 就是多重背包的一道典型例题，在题目中，每件武器有体积和重量两个限制条件。

对于多重背包，我们同样用前 i 个物品来划分阶段：

• dp[i][j] 表示 i 体积 j 重量下的最大火力。
• 转移方程：dp[i][j] = max(dp[i][j], dp[i-v[k]][j-g[k]] + t[k]);

同理，如果物品的数量是无限的，则正着 for，如果物品的数量是有限的，则倒着 for。

P1794 装备运输 的参考代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#include <bits/stdc++.h>
using namespace std;

int V, G, N, dp[510][510], v[510], g[510], t[510];

int main() {
    cin >> V >> G >> N;
    for (int i = 1; i <= N; ++i)
        cin >> t[i] >> v[i] >> g[i];
    for (int k = 1; k <= N; ++k)
        for (int i = V; i>= v[k]; i--)
            for (int j = G; j >= g[k]; j--)
                dp[i][j] = max(dp[i][j], dp[i-v[k]][j-g[k]] + t[k]);
    cout << dp[V][G];
    return 0;
}

如果把 01 背包和完全背包想像成填一个一维的表格，那么多重背包就在填一个二维的表格。我们需要保证表格的填写过程符合动态规划的阶段性，表格总是从一个方向往另一个方向填，填过的数字不会再次被修改（在没压维的情况下），这样才能保证状态无后效性。

动态规划题目能够划分出清晰的阶段，后一个阶段只依赖于前面的阶段，问题就解决了一大部分。

背包变型一：物品的相互依赖

P1064 金明的预算方案 描述了一种背包问题的变型：在此题中，物品不是简单的 1 个或多个，而是分为主件或附件，每个主件可以有 0 个、1 个或 2 个附件。

应该如何表示这种复杂的物品关系呢？其实，我们可以把物品的每种组合都枚举出来，因为附件数量最多为 2 个，所以情况就可以枚举出以下情况：

• 不选主件（当然也就没有附件）
• 选主件，不选附件
• 选主件+附件 1
• 选主件+附件 2
• 选主件+附件 1+附件 2

于是，我们就可以在处理主件的时候，把以上几种情况都比较一下，选最优的方案。

参考代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

#include <bits/stdc++.h>
using namespace std;

struct Node {
    int m;
    int w;
    int t;
};

int n, m;
vector<Node> va;
vector<vector<Node> > vb;
int dp[40000];

void updateDP(int i, int m, int w) {
    if (i-m >= 0) {
        dp[i] = max(dp[i], dp[i-m] + w);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    va.resize(m);
    vb.resize(m);
    for (int i = 0; i < m; ++i) {
        Node node;
        scanf("%d%d%d", &node.m, &node.w, &node.t);
        node.w = node.w*node.m; 
        va[i] = node;
        if (node.t != 0) {
            vb[node.t - 1].push_back(node);
        }
    }
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i < m; ++i) {
        // 只处理主件，附件与主体一并处理
        if (va[i].t == 0) {
            for (int j = n; j > 0; j--) {
                // 选主件，不选附件
                updateDP(j, va[i].m,va[i].w);
                // 选主件+附件 1
                if (vb[i].size() > 0) {
                    int money = va[i].m + vb[i][0].m;
                    int weight = va[i].w + vb[i][0].w;
                    updateDP(j, money, weight);
                }
                // 选主件+附件 2
                if (vb[i].size() == 2) {
                    int money = va[i].m + vb[i][1].m;
                    int weight = va[i].w + vb[i][1].w;
                    updateDP(j , money, weight);
                }
                // 选主件+附件 1+附件 2
                if (vb[i].size() == 2) {
                    int money = va[i].m + vb[i][0].m + vb[i][1].m;
                    int weight = va[i].w + vb[i][0].w + vb[i][1].w;
                    updateDP(j, money, weight);
                }
            }   
        }
    }
    cout << dp[n] << endl;
    return 0;
}

背包变型二：求最小值

有些时候，我们不是求背包能够装的物品的最大价值，而是求最小价值。例如 B3873 小杨买饮料 这题，此题我们可以把饮料的容量当作背包的容量，把饮料的价格当作价值，但是此题相对于标准的背包问题有两个变化：

• 1、题目希望求最小的费用，相当于背包所装的物品价值需要最低。
• 2、题目给定的背包容量不固定，而是“不低于 L”。

针对以上的变化，我们的状态定义虽然不变，用 dp[i][j] 表示前 i 种饮料在 j 容量下的最小价值，但是状态转移变成了：
dp[i][j] = min(dp[i-1][j-l[i]] + c[i], dp[i-1][j])

在这种情况下，初始的第 0 种饮料什么都喝的值为 0，即：dp[0][0] = 0。

但是其它的值就不能设置成 0 了，如果设置成 0，那么任何情况下 dp[i][j]就已经是最小的值了，就不能被更新了。我们需要把 dp[i][j]默认的值设置成“无穷大”，这样才可能更新出有意义的值。

在设置无穷大这件事情上，有一个使用 memset 的技巧，即：memset(dp, 0x7f, sizeof dp);，此技巧将每个字节都填充成了二进制的 01111111（即 0x7f），因为最高为是符号位，所以保留成 0。这种 memset 技巧虽然初始化的值比 INT_MAX 略小一点，但是写起来更快，另外在进行加法运算的时候，也不用担心结果溢出成负数。

以上方案解决了变化一。我们再来看变化二。

变化二使得答案不一定在 dp[i][L]，因为答案不一定是刚好 L 升，所以要取 L ~ L+max(l[i]) 这一段范围。这样就解决了变化二。

最后我们用滚动数组压维，然后因为是 01 背包（每个饮料只能选一次），我们压维之后需要倒着 for 循环背包大小。

以下是参考代码，代码中用 STL 的 min_element 来求最小值，读者也可以参考这种写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

/**
 * 01 背包问题的变化
 * 
 * 假设第 i 种饮料的费用是 c[i], 容量是 l[i]
 * dp[i][j] 表示用前 i 种饮料，凑成 j 升的最小费用。
 * 
 * 则，转移方程为：
 *  - dp[i][j] = min( dp[i-1][j-l[i]] + c[i] , dp[i-1][j] ) 
 * 
 * 因为 i 只与 i-1 相关，所以这一层可以压缩。转移方式优化为：
 *  - dp[j] = min(dp[j- l[i]] + c[i], dp[j])
 * 
 * 初使化：
 *  - dp[0] = 0;
 *  - dp[1-L] = memset(0x7f)
 * 
 * 其它：
 *  - 倒着 dp，因为每种饮料只能用一次
 *  - 最大值检查了一下，不会超 int，就不用 long long 了
 *  - 因为答案不一定是刚好 L 升，所以要取 L ~ L+max(l[i]) 这一段范围
 *  - 因为是取最小值，所以初使化设置成 0x7f7f7f7f（接近 21 亿，但是又没到 INT_MAX），
 *    这样运算不会超 int，又可以是较大值
 * 
 * Author: Tang Qiao
 */
#include <bits/stdc++.h>
using namespace std;

int dp[1010000], c[550], l[550], N, L, maxL;

int main() {
    ios::sync_with_stdio(0);       
    cin >> N >> L;
    for (int i = 0; i < N; ++i) {
        cin >> c[i] >> l[i];
        maxL = max(maxL, l[i]);
    }
    maxL += L;
    memset(dp, 0x7f, sizeof dp);
    dp[0] = 0;
    for (int i = 0; i < N; ++i) {
        for (int j = maxL; j - l[i] >= 0; --j) {
            dp[j] = min(dp[j], dp[j - l[i]] + c[i]);
        }
    }
    // 因为答案不一定是刚好 L 升，所以要取 L ~ L+max(l[i]) 这一段范围
    int ans = *min_element(dp+L, dp+maxL+1);
    if (ans == 0x7f7f7f7f) cout << "no solution" << endl;
    else cout << ans << endl;

    return 0;
}

以上代码虽然解决了问题，但是还有一点不完美，就是 dp 数组实在太大了。有没有可能 dp 数组更小呢？我们可以想到，因为每种饮料的价格都是正数，所以，如果有一个答案是超过 2*L 升的情况，同时它的价格极低，这种情况下，我们的答案就是只喝这一种饮料。不会出现超过 2*L 升，我们还叠加喝了两种饮料的情况。

我们可以反证：假如有一个答案是喝两种饮料，总容量超过 2*L 升，那么必定有一个饮料的容量是大于等于 L 升的。那么，我们只喝那个大于等于 L 升的饮料，肯定总价格更低。

所以，我们的优化方案就是：我们只需要把 dp 数组的大小开到 2*L 即 4000 即可（题目规定 L 最大为 2000）。在此优化方案下，我们再特判一下每个大于 L 升的饮料，看是不是更便宜。

以下是参考代码，时间和空间复杂度都更优：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include <bits/stdc++.h>
using namespace std;

int dp[4100], c[550], l[550], N, L;

int main() {
    ios::sync_with_stdio(0);       
    cin >> N >> L;
    for (int i = 0; i < N; ++i) {
        cin >> c[i] >> l[i];
    }
    memset(dp, 0x7f, sizeof dp);
    dp[0] = 0;
    for (int i = 0; i < N; ++i) {
        for (int j = 4000; j - l[i] >= 0; --j) {
            dp[j] = min(dp[j], dp[j - l[i]] + c[i]);
        }
    }
    int ans = *min_element(dp+L, dp+4000);
    // 如果单个饮料就可以超 L，则判断一下
    for (int i = 0; i < N; ++i)
        if (l[i] >= L) 
            ans = min(ans, c[i]);

    if (ans == 0x7f7f7f7f) cout << "no solution" << endl;
    else cout << ans << endl;

    return 0;
}

相关练习题目

推荐练习：

工作

2025 年是艰难的一年，上半年玩教具业务同比下滑，下半年尝试了一些营销推广，业务量有所稳定，但是赢亏承压。最后一年下来，虽然没亏钱，但是也没挣到钱。好在团队在持续成长，每个岗位的人都比去年有了长足的进步和成长。

2025 年也立项了好几个新项目，这些项目会陆续在 2026 年上线。前面的播种会积累到 2026 年的收获，所以未来怎么样，还是挺值得期待的。

读书

25 年一共读了 8 本书，以下是读书笔记：

• 个人投资的最佳实践 - 读《不落俗套的成功》
• 读《真需求》
• 投机与趋势投资 - 读《股票大作手操盘术》
• 但斌投资札记-读《时间的玫瑰》
• 理解大语言模型 - 读《图解 DeepSeek 技术》
• 理解 MCP -读《这就是 MCP》
• 和媒体共赢 - 读《广告的没落，公关的崛起》
• 读《疯狂的尿酸》

其中 《不落俗套的成功》 和 《广告的没落，公关的崛起》 是我今年最喜欢的两本书，一本书指导我开始更多关注配置，另一本书指导我如何做品牌。

25 年还开始订阅了纸质版本的《三联生活周刊》，加上雪球 App 每个月给我寄月刊。所以整个 2025 年的阅读量还是不小的。

感悟

今年思考人生，总结了 4 篇文章：

• 构建你的“多巴胺”系统
• 真相不重要
• 请为信息付费
• 我理解的保险产品

其中“多巴胺”系统那篇我自认为对我自己帮助最大，有效指导了我如何择友，如何工作，如何培养兴趣。

保险那篇文章，也让我理清了保险产品的购买思路，不再纠结要不要买保险，怎么买保险。

编程教学

今年继续在教小朋友编程，关于编程竞赛，今年又总结了如下文章：

• CSPJ 教学思考：贪心算法
• CSPJ 教学思考：动态规划
• CSPJ 教学思考：二分查找
• CSPJ 教学思考：并查集
• CSPJ 教学思考：模拟
• CSPJ 教学思考：枚举
• CSPJ 教学思考：数学题
• CSPJ 教学总结：STL
• CSPJ 教学总结：深度优先搜索（DFS）
• CSPJ 教学总结：树状数组
• GESP 核心考点

加上去年写的三篇，内容越来越丰富了：

• 五分钟弄懂 CSP-J
• CSPJ 教学思考：for 循环
• CSPJ 教学思考：宽度优先搜索

财务

2025 是财务收获的一年。

• 首先是年初公司允许大家出让期权，于是我卖了一些期权，补充了一些现金流。
• 2025 年初赶个 Deepseek 横空出世，整个港股大涨，我刚好又在那个时候有一些港币，配置了一些港股资产，于是买中了恒生高股息率，比亚迪，工商银行等股票，原来持有的腾讯也大涨。
• A 股这边，之前配置的建平从亏损变成浮盈；之前配置的 500 指数增强产品一下子也有 40% 的涨幅。
• 美股也不用说，标普和纳指继续涨，考虑到已经浮盈很多，我在 12 月将仓位全部清空了。
• 2025 年一直在定投黄金，最后也成功在一个相对低位（均价 700 多）配置了一定比例的黄金，现在也有 20% 的涨幅。

当然，2025 年配置的新能源组合也亏很多，特别是理想汽车，有 -30% 多的亏损。

更详细的业绩总结如下：

• 港股：
  • 腾讯（00700），成本 374，现价 599，+60%
  • 恒生高股息率（03110）
    • 第一笔：成本 23，现价 30，+30%
    • 第二笔：成本 31，现价 30，-2%
  • 工商银行，买入 5.4，卖出 6.07，含分红赢利约 15%
  • 新能源组合：
    • 理想汽车，-30%
    • 小鹏汽车，-4%
    • 小米，1%
    • 比亚迪，7%
• 美股：
  • 标普和纳指均清仓，整体收益约 10%
• 私募
  • 500 指增，+44%
  • 建平远航，+72%
• A 股
  • 招商银行，+11%
  • 红利 ETF 组合，+2%
  • 恒生科技 ETF，-6%
• 黄金：
  • 成本 795，现价 1071，+34%

尝鲜

24 小时血糖仪

今年戴了两次 24 小时的血糖仪，每次佩戴 14 天。我整体感觉很受用，它可以监测到不同食物和运动对血糖的影响。

然后我理解了两个事情：

• 一个是我之前饭后犯困，我大概也猜到是晕碳，现在戴上之后明显就能确认是这个原因。而且我尝试调整饮食之后，因为血糖上升慢，就不犯困了。
• 第二就是理解了饭后散步和遛弯为什么重要，对比饭后坐着和散步的血糖走势，我一下子就发现散步对降血糖的意义了。所以饭后走个 10 来分钟其实对身体的帮助是很大的。

另外这东西还有一个好处，就是会促进我轻度运动。我现在天气好的时候会尽量骑车上下班，因为这样我的血糖走势会很漂亮。

另外，我对比不同时段吃同样的水果对血糖的影响，明显餐后的影响更小，如下图：

我也总结了一些吃饭顺序的经验：

• 同样吃一颗橙子，餐前和餐后血糖上升速度和峰值差异很大。优先餐后吃水果，不要空腹吃。
• 同样是吃饭，先吃蔬菜和后吃蔬菜升血糖速度也差别很大。先吃蔬菜，最后吃碳水。
• 面食对血糖的提升是迅速的，少吃为妙。

3D打印和建模

公司因为需要，采购了拓竹的 3D 打印机，于是我有一段时间就很痴迷它。拓竹真的是国货之光，把原来只能极客使用的 3D 打印机做成了可以普及的消费品的品质，一些配平等复杂设置都不需要人工介入，机器自动就能完成。

我顺便还在Tinkercad 上学习了建模，然后利用自己学到的建模知识，帮老婆做了一个定制款的精油瓶。它主要可以完美适配我们家的桌面，并且做得很紧凑，可以放更多的瓶子。最后我买了一种松木质感的耗材，这样放在桌子上也很搭。

以下是设计稿截图：

以下是效果：

骑车

今年狠狠地试了一下骑行，但是没有花钱买装备。一方面是因为我的运动量不大，频率不高；另一方面也是希望想骑的时候可以随时骑，想放弃的时候就可以放弃，没有任何压力，共享单车月卡在这方面还是挺方便的。

最狠的一次，我花了周末一个下午绕三环骑了一圈（下图，一共 50 公里）。不过冬天骑行的体验不佳，已经断了有一个月了，希望天气暖和之后可以继续骑起来。

旅行

新疆

五一去了新疆，很值得去的一个地方。我们租了一辆理想 L8，驰骋在满是风力发电站的草原上，感觉非常放松。

希腊

暑假去了希腊。

• 欧洲的衰败让人感叹时代和周期的变化，当地有很多没人住的空置房（下图：我们下榻酒店附近的一处空置房）。
• 猫咪在希腊很受人待见，大街和公园上有很多猫咪。
• 在希腊吃了几天各种西餐之后，最后父母还是忍不住选择中餐，结果我们就把希腊的中餐馆吃了个遍。希腊的物价在欧洲相对低，一个菜大概 80 元人民币左右。
• 在希腊我也租了一辆车，是一辆 9 座的现代混动 Staria MPV，也非常好开。我们还乘坐渡轮（下图）把车运到了扎金索斯岛，在岛上放松了好几天。

沈阳

十一去了沈阳，就一个感受，物价实在太低太低，锅包肉大概 20 多块钱。租了一辆比亚迪的宋 Pro 混动，油耗特别低，每百公里油耗大概只有 4L。下图是我实际驾驶的数据，因为这辆车只能慢充，所以我一直在亏电情况下行驶，并没有充过电。

这也让我明白了比亚迪为什么出海那么厉害，这么低的油耗在能源较贵的欧洲，其实很有市场。

25 年的目标回顾

• 工作：硬件稳中有增，图书赢亏打正。带好图书业务。
  • ❎ 硬件既不稳，也不增。
  • ✅ 图书实际达成 60 分吧。图书赢亏基本打正了，但是要说有多好，还完全谈不上。
• 理财：做好配置，找到能拿 10 年的标的，并能坚定持有。
  • ✅ 配置工作基本完成。先拿两年看看，看自己拿不拿得住。
• 个人：读 6 本书。编程教学继续累进。
  • ✅ 最后读了 8 本书。编程教学写了 11 篇总结。

26 年的目标

• 工作：
  • 产品：今年种下的花，期待 26 年结果。AI 硬件拿到一些认知。
  • 运营：实践《广告的没落，公关的崛起》。
• 理财：
  • 不折腾，配置+再平衡。
• 个人：
  • 读 6 本书。
  • 俯卧撑能连续做 20 个。
  • 骑车绕四环一圈。

个人 Milestone

好象没啥特别能说的，如果非要有什么，就是产出了 《构建你的“多巴胺”系统》 这篇文章吧。

《疯狂的尿酸》是一本关于健康的科普书，来自于美国医学博士：戴维·珀尔马特，他是一位畅销书作家，写过《谷物大脑》和《菌群大脑》。

什么是尿酸

正常人体中的尿酸，2/3 是内源性的。尿酸是嘌呤的代谢产物，而嘌呤是细胞的重要组成部分，可以用来合成 DNA 和 RNA，人类的细胞因为不停地在分裂和衰老，死亡的细胞在被处理的时候就会产生尿酸。

另外 1/3 的尿酸来自于外部摄入的食物，包括动物内脏，海鲜，啤酒等。

果糖是一种特别的糖，它虽然不会造成血糖上升，但是会在代谢的时候产生尿酸。

尿酸会促进脂肪的产生

因为高尿酸与肥胖相关性很高，为了研究他们之间的因果关系，人们发现了“尿酸氧化酶”。这是一种存在于大多数动物体内的酶，能够迅速将尿酸排出体外，但是我们的人类祖先在几百万年的进化过程中，产生这个酶的基因被破坏了，变成了“假基因”。这就使得我们人类血液中的尿酸含量是其他哺乳动物的 3-10 倍。

当远古时代的人类吃下果糖后，果糖会在代谢过程中产生尿酸，而尿酸会打开人体的“脂肪开关”，帮助人体把果糖转化为脂肪。“从水果到脂肪”的生理机制帮助古代的灵长类动物能够度过漫长的、食物匮乏的冬天。

果糖

果糖是所有天然的碳水化合物中最甜的一种，天然的果糖只存在于水果和蜂蜜中，所以人类摄入得很少。而且水果中富含膳食纤维，可以延缓果糖被吸收的速度；而水果中富含的维生素 C 还有降低尿酸及促进尿酸排出的功能，所以吃水果对果糖的提升是很低的，代谢产生的尿酸也很少。

纯葡萄糖和果糖都是单糖（糖的最简单形式），而蔗糖是葡萄糖和果糖的组合，是一种双糖（两个分子连接在一起）。蔗糖进入人体后在小肠被分解，释放果糖和葡萄糖，然后被吸收。

果葡糖浆是一种以果糖为主的糖浆制品，果糖占比约 55%，葡萄糖占比 42%。最早是 1957 年由美国生物化学家 理查德·O 马歇尔 和 厄尔·R 科伊 生产出来，他们创造了一种酶，可以通过化学方法使玉米糖浆中的葡萄糖的结构重新排列，将其转化为果糖。

果葡糖浆从 20 世纪 70 年代开始流行，主要是因为其甜度比蔗糖高，价格又比蔗糖低，所以逐渐取代了蔗糖。到了 1984 年，可口可乐和百事可乐也都把各自品牌的饮料从添加蔗糖改为添加果葡糖浆。

果糖的升糖指数是所有天然糖中最低的，这意味着它不会直接导致血糖升高，也就不会刺激胰岛素的分泌，所以在一段时间内，人们把果糖视为一种“更安全”和“健康”的糖。但后来人们发现，相比于葡萄糖参与能量生成，果糖则参与能量储存，所以更容易让人肥胖。

果糖的代谢过程

果糖和葡萄糖除了一些化学键不同，其他结构几乎完全一样。然后，正是这微小的差异使得它们的代谢过程完全不同。

葡萄糖代谢的第一步（葡萄糖的磷酸化）是在葡萄糖激酶催化下分解，分解所释放的 ATP 也会在细胞中维持稳定的水平。ATP（三磷酸腺苷）是人体能量的来源。

果糖的代谢与葡萄糖完全不同。果糖在进入人体后，会迅速被血液吸收，然后被运输到肝脏中进行代谢。在肝细胞内，果糖激酶会开始工作，做出包括消耗 ATP 在内的一系列事情。果糖会消耗 ATP 的过程会带来一些下游效应，它会导致血液中的尿酸水平快速上升。由于果糖消耗了 ATP，细胞会发出信号：我们的能量快用完了。这会促使身体减缓新陈代谢以减少静息能量消耗。

除了消耗能量外，果糖还会触发脂肪的生成过程：肝脏中的果糖代谢会直接导致脂肪的产生：主要是以甘油三酯的形式存在，这是人体中最常见的脂肪存在形式。

AMP 活化蛋白激酶

AMP 活化蛋白激酶被激活时，它会向你的身体发出“狩猎状况良好”（即食物充足）的信号，你的身体就会让自己从储存脂肪转换为燃烧脂肪，帮助身体保持良好的狩猎状态。

AMP 活化蛋白激酶还可以帮助身体减少葡萄糖生成。二甲双胍就利用了这一点来实现降血糖。

与AMP 活化蛋白激酶对应的，还有一种让身体储存脂肪的酶，叫做腺苷单磷酸脱氨酶 2。动物在准备冬眠的时候，就会激活腺苷单磷酸脱氨酶 2 用于储存脂肪；在冬眠的时候，则切换到AMP 活化蛋白激酶用于燃烧脂肪。

而果糖代谢过程产生的尿酸，就是这两种酶的调节剂，尿酸能够抑制AMP 活化蛋白激酶，同时激活腺苷单磷酸脱氨酶 2 。

断食

作者推荐大家可以尝试 24 小时的断食，即：24 小时内不吃任何东西，且大量饮水。如果正在服用药物，务必继续服用。

我也见过一种 16：8 的轻断食方法：即 16 小时断食，8 小时进食。通常时间设置为中午 12 点-下午 8 点，或者上午 10 点到晚 6 点。

小结

本书主要揭示了果糖和尿酸在人体代谢中的核心原理，让我们更加关注饮食和内分泌的健康。