❌

阅读视图

发现新文章，点击刷新页面。

每日一题-最大化网格图中正方形空洞的面积🟡

✇LeetCode 每日一题题解

给你一个网格图，由 n + 2 条 横线段 和 m + 2 条 竖线段 组成，一开始所有区域均为 1 x 1 的单元格。

所有线段的编号从 1 开始。

给你两个整数 n 和 m 。

同时给你两个整数数组 hBars 和 vBars 。

  • hBars 包含区间 [2, n + 1] 内 互不相同 的横线段编号。
  • vBars 包含 [2, m + 1] 内 互不相同的 竖线段编号。

如果满足以下条件之一，你可以 移除 两个数组中的部分线段：

  • 如果移除的是横线段，它必须是 hBars 中的值。
  • 如果移除的是竖线段，它必须是 vBars 中的值。

请你返回移除一些线段后（可能不移除任何线段），剩余网格图中 最大正方形 空洞的面积，正方形空洞的意思是正方形 内部 不含有任何线段。

 

示例 1：

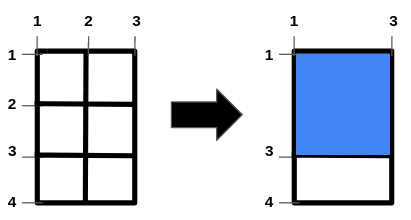
输入：n = 2, m = 1, hBars = [2,3], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2,3] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 2：

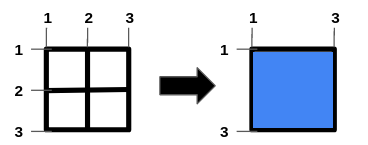
输入：n = 1, m = 1, hBars = [2], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,3] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 3：

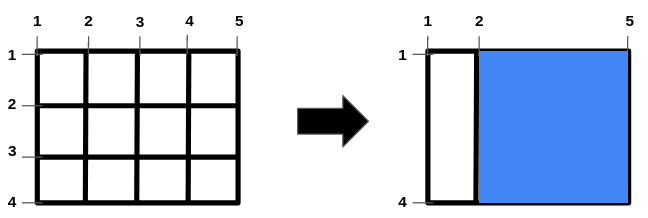
输入：n = 2, m = 3, hBars = [2,3], vBars = [2,3,4]
输出：9
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,5] 。
可以移除的横线段为 [2,3] ，竖线段为 [2,3,4] 。
一种得到最大正方形面积的方法是移除横线段 2、3 和竖线段 3、4 。
操作后得到的网格图如右图所示。
正方形空洞面积为 9。
无法得到面积大于 9 的正方形空洞。
所以答案为 9 。

 

提示：

  • 1 <= n <= 109
  • 1 <= m <= 109
  • 1 <= hBars.length <= 100
  • 2 <= hBars[i] <= n + 1
  • 1 <= vBars.length <= 100
  • 2 <= vBars[i] <= m + 1
  • hBars 中的值互不相同。
  • vBars 中的值互不相同。

不排序，线性时间复杂度（Python/Java/C++/Go）

✇LeetCode 每日一题题解
endlesscheng

阅读理解题，难度在读题上。

贪心地，删的线段越多，面积越大，那就先把所有能删的线段都删掉，计算最大的矩形，长宽分别是多少。

取长宽的最小值，即为正方形的边长（多删的线段撤销删除）。

以 $\textit{hBars}$ 为例：

  • 不删，最长长度是 $1$。
  • 删除一条线段，最长长度是 $2$。
  • 删除两条编号相邻的线段，最长长度是 $3$。
  • 删除三条编号连续的线段（例如 $2,3,4$），最长长度是 $4$。
  • 依此类推。

所以本题要做的是，把数组排序后，求最长连续递增子数组的长度加一。

正方形的边长是长宽的最小值，其平方即为正方形的面积。

优化前

###py

class Solution:
    # 返回 a 排序后的最长连续递增子数组的长度
    def f(self, a: List[int]) -> int:
        a.sort()
        mx = cnt = 0
        for i, x in enumerate(a):
            if i > 0 and x == a[i - 1] + 1:
                cnt += 1
            else:
                cnt = 1  # 重新计数
            mx = max(mx, cnt)
        return mx

    def maximizeSquareHoleArea(self, n: int, m: int, hBars: List[int], vBars: List[int]) -> int:
        side = min(self.f(hBars), self.f(vBars)) + 1
        return side * side

###java

class Solution {
    public int maximizeSquareHoleArea(int n, int m, int[] hBars, int[] vBars) {
        int side = Math.min(f(hBars), f(vBars)) + 1;
        return side * side;
    }

    // 返回 a 排序后的最长连续递增子数组的长度
    private int f(int[] a) {
        Arrays.sort(a);
        int mx = 1;
        int cnt = 1;
        for (int i = 1; i < a.length; i++) {
            if (a[i] == a[i - 1] + 1) {
                cnt++;
                mx = Math.max(mx, cnt);
            } else {
                cnt = 1; // 重新计数
            }
        }
        return mx;
    }
}

###cpp

class Solution {
    // 返回 a 排序后的最长连续递增子数组的长度
    int f(vector<int>& a) {
        ranges::sort(a);
        int mx = 1, cnt = 1;
        for (int i = 1; i < a.size(); i++) {
            if (a[i] == a[i - 1] + 1) {
                cnt++;
                mx = max(mx, cnt);
            } else {
                cnt = 1; // 重新计数
            }
        }
        return mx;
    }

public:
    int maximizeSquareHoleArea(int, int, vector<int>& hBars, vector<int>& vBars) {
        int side = min(f(hBars), f(vBars)) + 1;
        return side * side;
    }
};

###go

// 返回 a 排序后的最长连续递增子数组的长度
func f(a []int) (mx int) {
slices.Sort(a)
cnt := 0
for i, x := range a {
if i > 0 && x == a[i-1]+1 {
cnt++
} else {
cnt = 1 // 重新计数
}
mx = max(mx, cnt)
}
return mx
}

func maximizeSquareHoleArea(_, _ int, hBars, vBars []int) int {
side := min(f(hBars), f(vBars)) + 1
return side * side
}

复杂度分析

  • 时间复杂度：$\mathcal{O}(h\log h+v\log v)$，其中 $h$ 为 $\textit{hBars}$ 的长度，$v$ 为 $\textit{vBars}$ 的长度。
  • 空间复杂度：$\mathcal{O}(1)$。忽略排序的栈开销。

优化

用 128. 最长连续序列 的技巧优化，见 我的题解。

###py

class Solution:
    # 128. 最长连续序列
    def longestConsecutive(self, nums: List[int]) -> int:
        st = set(nums)  # 把 nums 转成哈希集合
        ans = 0
        for x in st:  # 遍历哈希集合
            if x - 1 in st:  # 如果 x 不是序列的起点，直接跳过
                continue
            # x 是序列的起点
            y = x + 1
            while y in st:  # 不断查找下一个数是否在哈希集合中
                y += 1
            # 循环结束后，y-1 是最后一个在哈希集合中的数
            ans = max(ans, y - x)  # 从 x 到 y-1 一共 y-x 个数
        return ans

    def maximizeSquareHoleArea(self, n: int, m: int, hBars: List[int], vBars: List[int]) -> int:
        side = min(self.longestConsecutive(hBars), self.longestConsecutive(vBars)) + 1
        return side * side

###java

class Solution {
    public int maximizeSquareHoleArea(int n, int m, int[] hBars, int[] vBars) {
        int side = Math.min(longestConsecutive(hBars), longestConsecutive(vBars)) + 1;
        return side * side;
    }

    // 128. 最长连续序列
    private int longestConsecutive(int[] nums) {
        Set<Integer> st = new HashSet<>();
        for (int num : nums) {
            st.add(num); // 把 nums 转成哈希集合
        }

        int ans = 0;
        for (int x : st) { // 遍历哈希集合
            if (st.contains(x - 1)) { // 如果 x 不是序列的起点，直接跳过
                continue;
            }
            // x 是序列的起点
            int y = x + 1;
            while (st.contains(y)) { // 不断查找下一个数是否在哈希集合中
                y++;
            }
            // 循环结束后，y-1 是最后一个在哈希集合中的数
            ans = Math.max(ans, y - x); // 从 x 到 y-1 一共 y-x 个数
        }
        return ans;
    }
}

###cpp

class Solution {
    // 128. 最长连续序列
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> st(nums.begin(), nums.end()); // 把 nums 转成哈希集合
        int ans = 0;
        for (int x : st) { // 遍历哈希集合
            if (st.contains(x - 1)) { // 如果 x 不是序列的起点，直接跳过
                continue;
            }
            // x 是序列的起点
            int y = x + 1;
            while (st.contains(y)) { // 不断查找下一个数是否在哈希集合中
                y++;
            }
            // 循环结束后，y-1 是最后一个在哈希集合中的数
            ans = max(ans, y - x); // 从 x 到 y-1 一共 y-x 个数
        }
        return ans;
    }

public:
    int maximizeSquareHoleArea(int, int, vector<int>& hBars, vector<int>& vBars) {
        int side = min(longestConsecutive(hBars), longestConsecutive(vBars)) + 1;
        return side * side;
    }
};

###go

// 128. 最长连续序列
func longestConsecutive(nums []int) (ans int) {
has := map[int]bool{}
for _, num := range nums {
has[num] = true // 把 nums 转成哈希集合
}

for x := range has { // 遍历哈希集合
if has[x-1] { // 如果 x 不是序列的起点，直接跳过
continue
}
// x 是序列的起点
y := x + 1
for has[y] { // 不断查找下一个数是否在哈希集合中
y++
}
// 循环结束后，y-1 是最后一个在哈希集合中的数
ans = max(ans, y-x) // 从 x 到 y-1 一共 y-x 个数
}
return
}

func maximizeSquareHoleArea(_, _ int, hBars, vBars []int) int {
side := min(longestConsecutive(hBars), longestConsecutive(vBars)) + 1
return side * side
}

复杂度分析

  • 时间复杂度：$\mathcal{O}(h+v)$，其中 $h$ 为 $\textit{hBars}$ 的长度，$v$ 为 $\textit{vBars}$ 的长度。
  • 空间复杂度：$\mathcal{O}(h+v)$。

相似题目

分类题单

如何科学刷题？

  1. 滑动窗口与双指针（定长/不定长/单序列/双序列/三指针/分组循环）
  2. 二分算法（二分答案/最小化最大值/最大化最小值/第K小）
  3. 单调栈（基础/矩形面积/贡献法/最小字典序）
  4. 网格图（DFS/BFS/综合应用）
  5. 位运算（基础/性质/拆位/试填/恒等式/思维）
  6. 图论算法（DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流）
  7. 动态规划（入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望）
  8. 常用数据结构（前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树）
  9. 数学算法（数论/组合/概率期望/博弈/计算几何/随机算法）
  10. 贪心与思维（基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造）
  11. 链表、树与回溯（前后指针/快慢指针/DFS/BFS/直径/LCA）
  12. 字符串（KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机）

我的题解精选（已分类）

欢迎关注 B站@灵茶山艾府

n、m参数不用考虑，只需对hBars、vBars排序遍历计算，0ms双百

✇LeetCode 每日一题题解
admiring-meninskyuli

Problem: 100138. 最大化网格图中正方形空洞的面积

[TOC]

思路

分析题意：

  • 抽掉一根线，则空出空间： 2

  • 若存在连续 l 根线，抽出后，空出空间为： l + 1

  • hBars.length、vBars.length 至少为1，即必有线被抽掉，至少有空间 2

因此，贪心思路来考虑：

  • 第一步、对 hBars 和 vBars 排序

  • 第二步、分别求出 hBars 和 vBars 的连续最长线段

  • 第三步、取 hBars 和 vBars 的连续最长线段两者的较小值，平方后返回

此题，n、m 两个参数可以不用到。

Code

执行用时分布0ms击败100.00%；消耗内存分布6.47MB击败100.00%

###C

int cmp(const void* a, const void* b) {
    return *(int*)a - *(int*)b;
}
int maxlen(int* lst, int len) {
    qsort(lst, len, sizeof(int), cmp);
    int ma = 2, l = 2;
    for (int i = 0; i < len - 1; ++ i)
        if (lst[i + 1] - lst[i] == 1) { if (++ l > ma) ma = l; }
        else l = 2;
    return ma;
}
int maximizeSquareHoleArea(int n, int m, int* hBars, int hBarsSize, int* vBars, int vBarsSize) {
    int h = maxlen(hBars, hBarsSize), v = maxlen(vBars, vBarsSize);
    return h < v ? h * h : v * v;
}

###Python3

class Solution:
    def maximizeSquareHoleArea(self, n: int, m: int, hBars: List[int], vBars: List[int]) -> int:
        def maxlen(lst):
            ma, l = 2, 2
            for x, y in pairwise(sorted(lst)):
                if y - x == 1: 
                    l += 1
                    ma = max(ma, l)
                else:
                    l = 2
            return ma
        return min(maxlen(hBars), maxlen(vBars)) ** 2

您若还有不同方法，欢迎贴在评论区，一起交流探讨！ ^_^

↓ 点个赞，点收藏，留个言，再划走，感谢您支持作者！ ^_^

【 排序】java双百 - 枚举差值为1

✇LeetCode 每日一题题解
heuristic-sutherlandoyz

Problem: 100138. 最大化网格图中正方形空洞的面积

[TOC]

1.png

解题方法

其实这个题没有看上去那么难

只需要排序之后取两个数组差值为1的最大个数即可

计算差值为一的元素个数是因为需要统计最大能切割出多大的正方形

（周赛wa三次真的要吐血了X_X）

复杂度

时间复杂度: $O(nlogn + mlogm)$ 主要取决于排序

Code

###Java

class Solution {
    public int maximizeSquareHoleArea(int n, int m, int[] hBars, int[] vBars) {
        int h = 1;
        int v = 1;
        Arrays.sort(hBars);
        Arrays.sort(vBars);
        int ht = 1;
        int vt = 1;
        for(int i = 1;i < hBars.length;i++){
            if(hBars[i] - hBars[i - 1] == 1) ht++;
            if(hBars[i] - hBars[i - 1] != 1){
                ht = 1;
            }
            h = Math.max(ht,h);
        }
        for(int i = 1;i < vBars.length;i++){
            if(vBars[i] - vBars[i - 1] == 1) vt++;
            if(vBars[i] - vBars[i - 1] != 1){
                vt = 1;
            }
            v = Math.max(vt,v);
        }
        int l = Math.min(v + 1,h + 1);
        return l * l;
    }
}

3D字体TextGeometry

✇掘金 前端
烛阴
1. 引入字体加载器 由于 TextGeometry 不是核心库的一部分，我们需要单独引入： 2. 加载 JSON 字体并创建 Three.js 不直接读取 .ttf，它读取的是专用的 JSON 字体

markstream-vue实战踩坑笔记

✇掘金 前端
桜吹雪
最近新开始做了一个ai对话的项目，打算重构一下老项目的markdown渲染和交互。老项目使用marked对md进行渲染成html，然后使用v-html渲染，搞到后面发现太多技术债了，所以打算换一个实现
❌