给定一个根为 root 的二叉树，每个节点的深度是 该节点到根的最短距离 。

返回包含原始树中所有 最深节点 的 最小子树 。

如果一个节点在 整个树 的任意节点之间具有最大的深度，则该节点是 最深的 。

一个节点的 子树 是该节点加上它的所有后代的集合。

 

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4]
输出：[2,7,4]
解释：
我们返回值为 2 的节点，在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意，节点 5、3 和 2 包含树中最深的节点，但节点 2 的子树最小，因此我们返回它。

示例 2：

输入：root = [1]
输出：[1]
解释：根节点是树中最深的节点。

示例 3：

输入：root = [0,1,3,null,2]
输出：[2]
解释：树中最深的节点为 2 ，有效子树为节点 2、1 和 0 的子树，但节点 2 的子树最小。

 

提示：

• 树中节点的数量在 [1, 500] 范围内。
• 0 <= Node.val <= 500
• 每个节点的值都是 独一无二 的。

 

注意：本题与力扣 1123 重复：https://leetcode.cn/problems/lowest-common-ancestor-of-deepest-leaves

前置题目：236. 二叉树的最近公共祖先。

视频讲解：二叉树的最近公共祖先【基础算法精讲 12】。

方法一：递归递归，有递有归

{:width=360px}

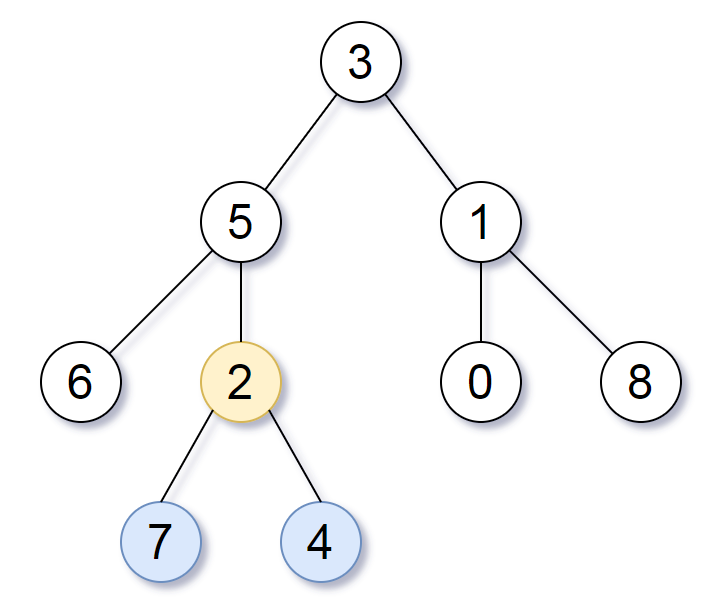
看上图（示例 1），这棵树的节点 $3,5,2$ 都是最深叶节点 $7,4$ 的公共祖先，但只有节点 $2$ 是最近的公共祖先。

上面视频中提到，如果我们要找的节点只在左子树中，那么最近公共祖先也必然只在左子树中。对于本题，如果左子树的最大深度比右子树的大，那么最深叶结点就只在左子树中，所以最近公共祖先也只在左子树中。

如果左右子树的最大深度一样呢？当前节点一定是最近公共祖先吗？

不一定。比如节点 $1$ 的左右子树最深叶节点 $0,8$ 的深度都是 $2$，但该深度并不是全局最大深度，所以节点 $1$ 并不能是答案。

根据以上讨论，正确做法如下：

1. 递归这棵二叉树，同时维护全局最大深度 $\textit{maxDepth}$。
2. 在「递」的时候往下传 $\textit{depth}$，用来表示当前节点的深度。
3. 在「归」的时候往上传当前子树最深叶节点的深度。
4. 设左子树最深叶节点的深度为 $\textit{leftMaxDepth}$，右子树最深叶节点的深度为 $\textit{rightMaxDepth}$。如果 $\textit{leftMaxDepth}=\textit{rightMaxDepth}=\textit{maxDepth}$，那么更新答案为当前节点。⚠注意：这并不代表我们立刻找到了答案，如果后面发现了更深的叶节点，答案还会更新。

class Solution:
    def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        max_depth = -1  # 全局最大深度
        ans = None

        def dfs(node: Optional[TreeNode], depth: int) -> int:
            nonlocal ans, max_depth
            if node is None:
                max_depth = max(max_depth, depth)  # 维护全局最大深度
                return depth

            left_max_depth = dfs(node.left, depth + 1)  # 获取左子树最深叶节点的深度
            right_max_depth = dfs(node.right, depth + 1)  # 获取右子树最深叶节点的深度

            if left_max_depth == right_max_depth == max_depth:
                ans = node  # node 可能是答案

            return max(left_max_depth, right_max_depth)  # 当前子树最深叶节点的深度

        dfs(root, 0)
        return ans

class Solution {
    private int maxDepth = -1; // 全局最大深度
    private TreeNode ans;

    public TreeNode subtreeWithAllDeepest(TreeNode root) {
        dfs(root, 0);
        return ans;
    }

    private int dfs(TreeNode node, int depth) {
        if (node == null) {
            maxDepth = Math.max(maxDepth, depth); // 维护全局最大深度
            return depth;
        }

        int leftMaxDepth = dfs(node.left, depth + 1); // 获取左子树最深叶节点的深度
        int rightMaxDepth = dfs(node.right, depth + 1); // 获取右子树最深叶节点的深度

        if (leftMaxDepth == rightMaxDepth && leftMaxDepth == maxDepth) {
            ans = node; // node 可能是答案
        }

        return Math.max(leftMaxDepth, rightMaxDepth); // 当前子树最深叶节点的深度
    }
}

class Solution {
public:
    TreeNode* subtreeWithAllDeepest(TreeNode* root) {
        int max_depth = -1; // 全局最大深度
        TreeNode* ans;

        auto dfs = [&](this auto&& dfs, TreeNode* node, int depth) {
            if (node == nullptr) {
                max_depth = max(max_depth, depth); // 维护全局最大深度
                return depth;
            }

            int left_max_depth = dfs(node->left, depth + 1); // 获取左子树最深叶节点的深度
            int right_max_depth = dfs(node->right, depth + 1); // 获取右子树最深叶节点的深度

            if (left_max_depth == right_max_depth && left_max_depth == max_depth) {
                ans = node; // node 可能是答案
            }

            return max(left_max_depth, right_max_depth); // 当前子树最深叶节点的深度
        };

        dfs(root, 0);
        return ans;
    }
};

func subtreeWithAllDeepest(root *TreeNode) (ans *TreeNode) {
    maxDepth := -1 // 全局最大深度

    var dfs func(*TreeNode, int) int
    dfs = func(node *TreeNode, depth int) int {
        if node == nil {
            maxDepth = max(maxDepth, depth) // 维护全局最大深度
            return depth
        }

        leftMaxDepth := dfs(node.Left, depth+1) // 获取左子树最深叶节点的深度
        rightMaxDepth := dfs(node.Right, depth+1) // 获取右子树最深叶节点的深度

        if leftMaxDepth == rightMaxDepth && leftMaxDepth == maxDepth {
            ans = node // node 可能是答案
        }

        return max(leftMaxDepth, rightMaxDepth) // 当前子树最深叶节点的深度
    }

    dfs(root, 0)
    return
}

var subtreeWithAllDeepest = function(root) {
    let maxDepth = -1; // 全局最大深度
    let ans = null;

    function dfs(node, depth) {
        if (node === null) {
            maxDepth = Math.max(maxDepth, depth); // 维护全局最大深度
            return depth;
        }

        const leftMaxDepth = dfs(node.left, depth + 1); // 获取左子树最深叶节点的深度
        const rightMaxDepth = dfs(node.right, depth + 1); // 获取右子树最深叶节点的深度

        if (leftMaxDepth === rightMaxDepth && leftMaxDepth === maxDepth) {
            ans = node; // node 可能是答案
        }

        return Math.max(leftMaxDepth, rightMaxDepth); // 当前子树最深叶节点的深度
    }

    dfs(root, 0);
    return ans;
};

复杂度分析

• 时间复杂度：$\mathcal{O}(n)$。每个节点都会恰好访问一次。
• 空间复杂度：$\mathcal{O}(n)$。最坏情况下，二叉树是一条链，递归需要 $\mathcal{O}(n)$ 的栈空间。

方法二：自底向上

也可以不用全局变量，而是把每棵子树都看成是一个「子问题」，即对于每棵子树，我们需要知道：

• 这棵子树最深叶结点的深度。这里是指叶子在这棵子树内的深度，而不是在整棵二叉树的视角下的深度。相当于这棵子树的高度。
• 这棵子树的最深叶结点的最近公共祖先 $\textit{lca}$。

分类讨论：

• 设子树的根节点为 $\textit{node}$，$\textit{node}$ 的左子树的高度为 $\textit{leftHeight}$，$\textit{node}$ 的右子树的高度为 $\textit{rightHeight}$。
• 如果 $\textit{leftHeight} > \textit{rightHeight}$，那么子树的高度为 $\textit{leftHeight} + 1$，$\textit{lca}$ 是左子树的 $\textit{lca}$。
• 如果 $\textit{leftHeight} < \textit{rightHeight}$，那么子树的高度为 $\textit{rightHeight} + 1$，$\textit{lca}$ 是右子树的 $\textit{lca}$。
• 如果 $\textit{leftHeight} = \textit{rightHeight}$，那么子树的高度为 $\textit{leftHeight} + 1$，$\textit{lca}$ 就是 $\textit{node}$。反证法：如果 $\textit{lca}$ 在左子树中，那么 $\textit{lca}$ 不是右子树的最深叶结点的祖先，这不对；如果 $\textit{lca}$ 在右子树中，那么 $\textit{lca}$ 不是左子树的最深叶结点的祖先，这也不对；如果 $\textit{lca}$ 在 $\textit{node}$ 的上面，那就不符合「最近」的要求。所以 $\textit{lca}$ 只能是 $\textit{node}$。

class Solution:
    def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        def dfs(node: Optional[TreeNode]) -> Tuple[int, Optional[TreeNode]]:
            if node is None:
                return 0, None

            left_height, left_lca = dfs(node.left)
            right_height, right_lca = dfs(node.right)

            if left_height > right_height:  # 左子树更高
                return left_height + 1, left_lca
            if left_height < right_height:  # 右子树更高
                return right_height + 1, right_lca
            return left_height + 1, node  # 一样高

        return dfs(root)[1]

class Solution {
    private record Pair(int height, TreeNode lca) {}

    public TreeNode subtreeWithAllDeepest(TreeNode root) {
        return dfs(root).lca;
    }

    private Pair dfs(TreeNode node) {
        if (node == null) {
            return new Pair(0, null);
        }

        Pair left = dfs(node.left);
        Pair right = dfs(node.right);

        if (left.height > right.height) { // 左子树更高
            return new Pair(left.height + 1, left.lca);
        }
        if (left.height < right.height) { // 右子树更高
            return new Pair(right.height + 1, right.lca);
        }
        return new Pair(left.height + 1, node); // 一样高
    }
}

class Solution {
    pair<int, TreeNode*> dfs(TreeNode* node) {
        if (node == nullptr) {
            return {0, nullptr};
        }

        auto [left_height, left_lca] = dfs(node->left);
        auto [right_height, right_lca] = dfs(node->right);

        if (left_height > right_height) { // 左子树更高
            return {left_height + 1, left_lca};
        }
        if (left_height < right_height) { // 右子树更高
            return {right_height + 1, right_lca};
        }
        return {left_height + 1, node}; // 一样高
    }

public:
    TreeNode* subtreeWithAllDeepest(TreeNode* root) {
        return dfs(root).second;
    }
};

func dfs(node *TreeNode) (int, *TreeNode) {
    if node == nil {
        return 0, nil
    }

    leftHeight, leftLCA := dfs(node.Left)
    rightHeight, rightLCA := dfs(node.Right)

    if leftHeight > rightHeight { // 左子树更高
        return leftHeight + 1, leftLCA
    }
    if leftHeight < rightHeight { // 右子树更高
        return rightHeight + 1, rightLCA
    }
    return leftHeight + 1, node // 一样高
}

func subtreeWithAllDeepest(root *TreeNode) *TreeNode {
    _, lca := dfs(root)
    return lca
}

function dfs(node) {
    if (node === null) {
        return [0, null];
    }

    const [leftHeight, leftLca] = dfs(node.left);
    const [rightHeight, rightLca] = dfs(node.right);

    if (leftHeight > rightHeight) { // 左子树更高
        return [leftHeight + 1, leftLca];
    }
    if (leftHeight < rightHeight) { // 右子树更高
        return [rightHeight + 1, rightLca];
    }
    return [leftHeight + 1, node]; // 一样高
}

var subtreeWithAllDeepest = function(root) {
    return dfs(root, 0)[1];
};

复杂度分析

• 时间复杂度：$\mathcal{O}(n)$。每个节点都会恰好访问一次。
• 空间复杂度：$\mathcal{O}(n)$。最坏情况下，二叉树是一条链，递归需要 $\mathcal{O}(n)$ 的栈空间。

分类题单

如何科学刷题？

1. 滑动窗口与双指针（定长/不定长/单序列/双序列/三指针/分组循环）
2. 二分算法（二分答案/最小化最大值/最大化最小值/第K小）
3. 单调栈（基础/矩形面积/贡献法/最小字典序）
4. 网格图（DFS/BFS/综合应用）
5. 位运算（基础/性质/拆位/试填/恒等式/思维）
6. 图论算法（DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流）
7. 动态规划（入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望）
8. 常用数据结构（前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树）
9. 数学算法（数论/组合/概率期望/博弈/计算几何/随机算法）
10. 贪心与思维（基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造）
11. 链表、树与回溯（前后指针/快慢指针/DFS/BFS/直径/LCA）
12. 字符串（KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机）

我的题解精选（已分类）

欢迎关注 B站@灵茶山艾府

看了下下面的题解，除了官方题解用多个返回值只遍历了一次，其他题解大都反复计算深度，其实复杂度是O(nlogn)
本题解进行一次遍历得到结果

主要思想：

在一次遍历深度的过程中，找到左右子树深度都为最大值的节点记录下来

class Solution {
  private int maxDeep = Integer.MIN_VALUE;
  private TreeNode result;
  public TreeNode subtreeWithAllDeepest(TreeNode root) {
    maxDeep(root, 0);
    return result;
  }
  private int maxDeep(TreeNode node, int deep) {
    if (node == null) {
      return deep;
    }
    int left = maxDeep(node.left, deep+1);
    int right = maxDeep(node.right, deep+1);
    int currentMax = Math.max(left, right);
    maxDeep = Math.max(maxDeep, currentMax);
    if (left == maxDeep && right == maxDeep) {
      result = node;
    }
    return currentMax;
  }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户

class Solution {
    // 思路：从每个树开始，获得当前节点的左右子树的最大深度
    // 深度相同，说明最深的节点在这个节点两边，那这个节点就是结果
    // 如果深度不相同，则去深度大的子树继续判断，最终就能得到结果
    public TreeNode subtreeWithAllDeepest(TreeNode root) {
        if (root == null) return root;

        // 获取当前节点的左右子树的最大深度
        int leftMaxDepth = getMaxDepth(root.left);
        int rightMaxDepth = getMaxDepth(root.right);

        // 如果两边最大深度相同，则这个节点就是结果
        if (leftMaxDepth == rightMaxDepth) return root;

        // 不相等，那就去深度大的子树那边继续找
        if (leftMaxDepth > rightMaxDepth){
            return subtreeWithAllDeepest(root.left);
        }

        return subtreeWithAllDeepest(root.right);
    }

    public int getMaxDepth(TreeNode root){
        if (root == null) return 0;

        return Math.max(getMaxDepth(root.left), getMaxDepth(root.right)) + 1;
    }
}

本文大纲 今天来看一道前端面试的代码输出题。 面试官提供了一段 Javascript 代码，要求给出这段代码运行后的输出结果。 先分析这道题前，先补充两个个前置知识点。 知识点一：对象的常规属性 (p

^ 关注我，带你一起学GIS ^ 前言 在之前的文章中讲了如何使用GDAL或者ogr2ogr工具将txt以及csv文本数据转换为Shp格式，本篇教程在之前一系列文章的基础上讲解如何使用GDAL 空间关

Emscripten 是一个基于 LLVM/Clang 的开源编译器工具链，本文介绍Emscripten安装方法、解释常用命令，并阐述其工作原理。

• 知识点：动态规划
• 时间复杂度：O(n*m)；n，m 分别为两个序列的长度。

动态规划题目一般要先想好两个问题：

• 状态如何定义。
• 状态之间如何转移。

对于该题，最终目标是在分别两个序列中选取等长且非空的子序列，使得两个子序列的点积最大。
即，在 nums1 的前 n 个数中，在 nums2 的前 m 个数字中分别选取等长且非空的子序列， 使其点积最大。
推而广之，我们可以将问题表示为，在nums1的前 x (x <= n)个数字中，在nums2的前y(y <= m)个数字中，分别选取等长且非空的子序列， 使其点积最大。
为了方便，我们用 f(x, y) 表示子问题的最优方案的点积。
当(x, y) = (n,m) 时，f(x,y) 就是最终答案。

状态转移主要是分析状态之间的关联或差异，利用小问题的解高效的构造大问题的解。
来思考下该题状态如何转移，该题的特点是小问题总是为大问题的前缀，总是可以向小问题中追加数字得到一个大问题。
设 nx = nums1[x]，ny = nums2[y]。
f(x,y) 可能由以下几个状态转移得到：

• 向 f(x-1, y-1) 追加 nx,ny 获得 f(x, y)。
• 向 f(x, y-1) 追加 ny 获得 f(x, y)。
• 向 f(x-1, y) 追加 nx 获得 f(x,y)。

当然，也可以同时追加多个数字，由更小的问题获得 f(x, y)，但这本质上还是通过上述三种子问题间接转移过来的。
那么，为何f(x-1，y-1) 不能用 f(x-1, y) 或者 f(x, y-1) 间接转移过来呢？因为在求解过程中要考虑nx 和 ny 在对应位置的情况。
总结一下，该题的状态方程如下：
$$
f(x,y) = max \left{ \begin{array}{c}
nxny&, 有且只有 nx，ny\
nxny + f(x-1, y-1)&, 包含 nx，ny \
f(x, y-1)&, 不包含 nx \
f(x-1, y)&, 不包含 ny \
f(x-1, y-1)&, 不包含 nx，ny\
\end{array}\right.
$$

###cpp

class Solution {
public:
    int maxDotProduct(vector<int>& nums1, vector<int>& nums2) {
        int dp[501][501];
        for(int i = 0; i <= nums1.size(); i++) {
            for(int j = 0; j <= nums2.size(); j++) {
                dp[i][j] = -1000*1000*500;
            }
        }
        for(int i = 1; i <= nums1.size(); i++) {
            for(int j = 1; j <= nums2.size(); j++) {
                int a = nums1[i-1];
                int b = nums2[j-1];
                dp[i][j] = max(dp[i][j], a*b);
                dp[i][j] = max(dp[i][j], dp[i-1][j-1] + a*b);
                dp[i][j] = max(dp[i][j], dp[i-1][j-1]);
                dp[i][j] = max(dp[i][j], dp[i-1][j]);
                dp[i][j] = max(dp[i][j], dp[i][j-1]);
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};

如果感觉有点意思，可以关注👏HelloNebula👏

• 分享周赛题解
• 分享计算机专业课知识
• 分享C++相关岗位面试题
• 分享专业书籍PDF

一个完全在浏览器里运行的 AI 推理方案，不需要服务器，不需要后端，打开网页就能用。wllama 的出现，真的让这一切变成了可能。于是就有了这个项目

vue 表格 vxe-table 加载数据的几种方式，更新数据的用法，vue 最强大的表格组件，支持 vue2 和 vue3，功能太多，这里介绍基础用法 https://vxetable.cn 双向绑

用react开发一个antd mobile组件,页面上有多个高度不等的div元素,每个div底部都有一个「核对」按钮。当div的高度大于屏幕高度的时候，就要将这个div底部的「核对」按钮锁定在页面底部

本文简要梳理了 JavaScript 中 ==、===、Object.is 及 null、undefined、undeclared 的核心区别，帮助开发者正确理解比较规则与数据语义。

这份清单覆盖项目配置、模块导入导出、路径解析、第三方包兼容四大核心场景，为避开跨模块规范的常见问题。 一、 项目基础配置避坑 明确模块类型，避免自动切换混乱 Node.js 默认 .js 文件为 CJ

VitePress 大型 Markdown 文件构建失败问题：Element is missing end tag

核心区别概述 在 Node.js 和前端项目中，package.json 文件是项目的"身份证"和"配置清单"，其中的 dependencies（生产依赖）和 devDependencies（开发依赖

快看这个男人叫小帅！他写了一篇文章《万字解析——我为什么全平台最帅气的掘友》！开个玩笑，2025年鸽子王何贤相对大家说的话都在这个年终总结里面了

本文基于真实业务场景，围绕 Hooks 与组件封装展开，完整记录了从需求拆解、设计思路到最终落地的全过程。文章重点介绍了如何抽象通用能力、设计合理的 API、规避常见的 Hooks 使用误区，并给出了

一、为什么有了 TypeScript 还需要 Zod？ 本质区别 TypeScript Zod 作用时机 编译时 运行时 编译后 类型信息完全擦除 验证逻辑保留 保护范围 你写的代码 外部进来的数据

前端开发一直有一个老大难的问题，那就是——瀑布流布局。 效果需求并不复杂：卡片错落，参差有致，看起来高级，滚动起来流畅。 就是这样一个看似简单的效果，其实已经困扰了前端开发者好多年。