阅读视图
每日一题-给 N x 3 网格图涂色的方案数🔴
你有一个 n x 3 的网格图 grid ,你需要用 红,黄,绿 三种颜色之一给每一个格子上色,且确保相邻格子颜色不同(也就是有相同水平边或者垂直边的格子颜色不同)。
给你网格图的行数 n 。
请你返回给 grid 涂色的方案数。由于答案可能会非常大,请你返回答案对 10^9 + 7 取余的结果。
示例 1:
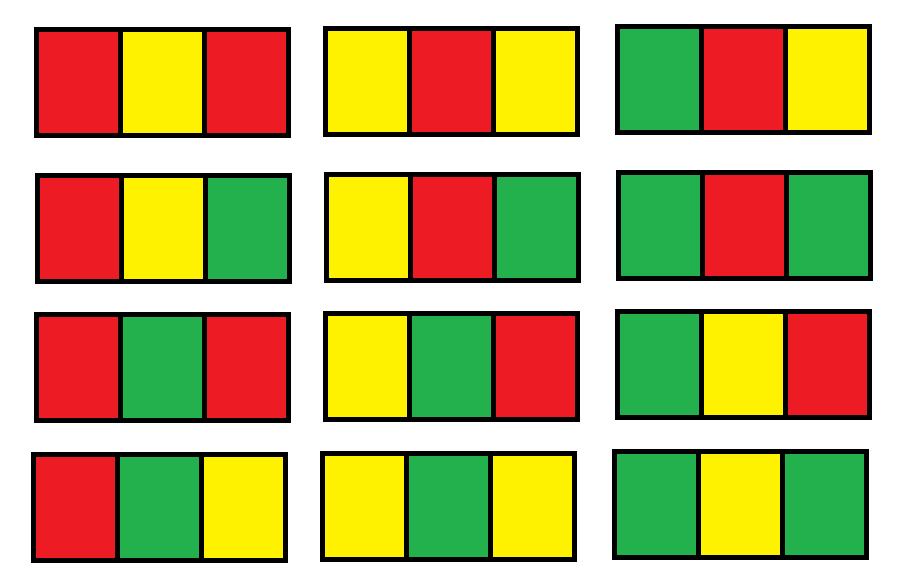
输入:n = 1 输出:12 解释:总共有 12 种可行的方法:
示例 2:
输入:n = 2 输出:54
示例 3:
输入:n = 3 输出:246
示例 4:
输入:n = 7 输出:106494
示例 5:
输入:n = 5000 输出:30228214
提示:
n == grid.lengthgrid[i].length == 31 <= n <= 5000
三种方法:记忆化搜索/递推/矩阵快速幂(Python/Java/C++/Go)
方法一:记忆化搜索(轮廓线 DP)
考虑暴力搜索,枚举每个格子涂哪种颜色。
从下往上涂色(这样可以在多组测试数据间复用记忆化的结果),我们需要知道:
- 当前在给哪个格子涂色?用 $(i,j)$ 表示,即 $i$ 行 $j$ 列。
- $i+1$ 行具体怎么涂色?用 $\textit{preRow}$ 表示。$(i,j)$ 的颜色不能等于 $(i+1,j)$ 的颜色。
- $i$ 行具体怎么涂色?用 $\textit{curRow}$ 表示。$(i,j)$ 的颜色不能等于 $(i,j-1)$ 的颜色。
三种颜色分别用 $0,1,2$ 表示,存储一个格子的颜色信息需要 $2$ 个比特位,一行的颜色就需要 $2\cdot 3 = 6$ 个比特位。
注意取模。为什么可以在中途取模?原理见 模运算的世界:当加减乘除遇上取模。
###py
MOD = 1_000_000_007
# (i, j):当前位置
# pre_row:上一行(i+1 行)的颜色
# cur_row:当前这一行已填入的颜色
@cache # 缓存装饰器,避免重复计算 dfs(一行代码实现记忆化)
def dfs(i: int, j: int, pre_row: int, cur_row: int) -> int:
if i == 0: # 所有格子都已涂色
return 1 # 找到一个合法方案
if j == 3: # i 行已涂色
# 开始对 i-1 行涂色,cur_row 变成 pre_row
return dfs(i - 1, 0, cur_row, 0)
res = 0
for color in range(3): # 枚举 (i, j) 的颜色 color
# 不能和下面相邻格子 (i+1, j) 颜色相同
# 不能和左侧相邻格子 (i, j-1) 颜色相同
if pre_row and color == pre_row >> (j * 2) & 3 or \
j and color == cur_row >> ((j - 1) * 2) & 3:
continue
res += dfs(i, j + 1, pre_row, cur_row | (color << (j * 2)))
return res % MOD
class Solution:
def numOfWays(self, n: int) -> int:
return dfs(n, 0, 0, 0) # 从最后一行开始涂色
###java
class Solution {
private static final int MOD = 1_000_000_007;
// 全局 memo,记忆化的内容可以在不同测试数据间共享
private static Map<Integer, Integer> memo = new HashMap<>();
public int numOfWays(int n) {
return dfs(n, 0, 0, 0);
}
// (i, j):当前位置
// preRow:上一行(i+1 行)的颜色
// curRow:当前这一行已填入的颜色
private int dfs(int i, int j, int preRow, int curRow) {
if (i == 0) { // 所有格子都已涂色
return 1; // 找到一个合法方案
}
if (j == 3) { // i 行已涂色
// 开始对 i-1 行涂色,curRow 变成 preRow
return dfs(i - 1, 0, curRow, 0);
}
// 参数压缩到一个 int 中
int key = (i << 14) | (j << 12) | (preRow << 6) | curRow;
if (memo.containsKey(key)) { // 之前计算过
return memo.get(key);
}
int res = 0;
for (int color = 0; color < 3; color++) { // 枚举 (i, j) 的颜色 color
if (preRow > 0 && color == (preRow >> (j * 2) & 3) || // 不能和下面相邻格子 (i+1, j) 颜色相同
j > 0 && color == (curRow >> ((j - 1) * 2) & 3)) { // 不能和左侧相邻格子 (i, j-1) 颜色相同
continue;
}
res = (res + dfs(i, j + 1, preRow, curRow | (color << (j * 2)))) % MOD;
}
memo.put(key, res); // 记忆化
return res;
}
}
###cpp
constexpr int MOD = 1'000'000'007;
// 全局 memo,记忆化的内容可以在不同测试数据间共享
unordered_map<int, int> memo;
// (i, j):当前位置
// pre_row:上一行(i+1 行)的颜色
// cur_row:当前这一行已填入的颜色
int dfs(int i, int j, int pre_row, int cur_row) {
if (i == 0) { // 所有格子都已涂色
return 1; // 找到一个合法方案
}
if (j == 3) { // i 行已涂色
// 开始对 i-1 行涂色,cur_row 变成 pre_row
return dfs(i - 1, 0, cur_row, 0);
}
// 参数压缩到一个 int 中
int key = (i << 14) | (j << 12) | (pre_row << 6) | cur_row;
if (memo.contains(key)) { // 之前计算过
return memo[key];
}
int res = 0;
for (int color = 0; color < 3; color++) { // 枚举 (i, j) 的颜色 color
if (pre_row > 0 && color == (pre_row >> (j * 2) & 3) || // 不能和下面相邻格子 (i+1, j) 颜色相同
j > 0 && color == (cur_row >> ((j - 1) * 2) & 3)) { // 不能和左侧相邻格子 (i, j-1) 颜色相同
continue;
}
res = (res + dfs(i, j + 1, pre_row, cur_row | (color << (j * 2)))) % MOD;
}
memo[key] = res; // 记忆化
return res;
}
class Solution {
public:
int numOfWays(int n) {
return dfs(n, 0, 0, 0);
}
};
###go
const mod = 1_000_000_007
type tuple struct{ i, j, preRow, curRow int }
// 全局 memo,记忆化的内容可以在不同测试数据间共享
var memo = map[tuple]int{}
// (i, j):当前位置
// preRow:上一行(i+1 行)的颜色
// curRow:当前这一行已填入的颜色
func dfs(i, j, preRow, curRow int) int {
if i == 0 { // 所有格子都已涂色
return 1 // 找到一个合法方案
}
if j == 3 { // i 行已涂色
// 开始对 i-1 行涂色,curRow 变成 preRow
return dfs(i-1, 0, curRow, 0)
}
t := tuple{i, j, preRow, curRow}
if res, ok := memo[t]; ok { // 之前计算过
return res
}
res := 0
for color := range 3 { // 枚举 (i, j) 的颜色 color
if preRow > 0 && color == preRow>>(j*2)&3 || // 不能和下面相邻格子 (i+1, j) 颜色相同
j > 0 && color == curRow>>((j-1)*2)&3 { // 不能和左侧相邻格子 (i, j-1) 颜色相同
continue
}
res = (res + dfs(i, j+1, preRow, curRow|color<<(j*2))) % mod
}
memo[t] = res // 记忆化
return res
}
func numOfWays(n int) int {
return dfs(n, 0, 0, 0)
}
复杂度分析
- 时间复杂度:$\mathcal{O}(nmk^{2m+1})$,其中 $m=3$ 是列数,$k=3$ 是颜色数。由于存在大量不合法的状态,复杂度不会跑满。
- 空间复杂度:$\mathcal{O}(nmk^{2m})$。
方法二:递推
回顾方法一,总体上看,DP 过程是一个线性递推(从 $(n-1)\times 3$ 网格图最后一行的所有涂色方案线性转移到 $n\times 3$ 网格图的最后一行),所以必然有线性递推式。
定义 $f[n]$ 表示给 $n\times 3$ 网格图涂色的方案数。
根据 Berlekamp-Massey 算法,用方法一求出 $f$ 的连续若干项(具体多少在文章中有解释,本题只需 $4$ 项),就可以用 Berlekamp-Massey 算法直接得到线性递推式
$$
f[i] = 5\cdot f[i-1]-2\cdot f[i-2] \ \ (i \ge 3)
$$
初始值 $f[1] = 12,\ f[2] = 54$。
也可以倒推出 $f[0]=3$,把 $f[0]$ 和 $f[1]$ 作为初始值。
###py
class Solution:
def numOfWays(self, n: int) -> int:
MOD = 1_000_000_007
f = [0] * (n + 1)
f[0] = 3
f[1] = 12
for i in range(2, n + 1):
f[i] = (f[i - 1] * 5 - f[i - 2] * 2) % MOD
return f[n]
###java
class Solution {
public int numOfWays(int n) {
final int MOD = 1_000_000_007;
int[] f = new int[n + 1];
f[0] = 3;
f[1] = 12;
for (int i = 2; i <= n; i++) {
f[i] = (int) ((f[i - 1] * 5L - f[i - 2] * 2L) % MOD); // 注意这里有减法,结果可能是负数
}
return (f[n] + MOD) % MOD; // 保证结果非负
}
}
###cpp
class Solution {
public:
int numOfWays(int n) {
constexpr int MOD = 1'000'000'007;
vector<int> f(n + 1);
f[0] = 3;
f[1] = 12;
for (int i = 2; i <= n; i++) {
f[i] = (f[i - 1] * 5LL - f[i - 2] * 2LL) % MOD; // 注意这里有减法,结果可能是负数
}
return (f[n] + MOD) % MOD; // 保证结果非负
}
};
###go
func numOfWays(n int) int {
const mod = 1_000_000_007
f := make([]int, n+1)
f[0] = 3
f[1] = 12
for i := 2; i <= n; i++ {
f[i] = (f[i-1]*5 - f[i-2]*2) % mod // 注意这里有减法,结果可能是负数
}
return (f[n] + mod) % mod // 保证结果非负
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n)$。
- 空间复杂度:$\mathcal{O}(n)$。注:可以用滚动变量优化至 $\mathcal{O}(1)$。
方法三:矩阵快速幂
把方法二的递推式用矩阵乘法表示,即
$$
\begin{bmatrix}
f[i] \
f[i-1] \
\end{bmatrix}
= \begin{bmatrix}
5 & -2 \
1 & 0 \
\end{bmatrix}
\begin{bmatrix}
f[i-1] \
f[i-2] \
\end{bmatrix}
$$
把上式中的三个矩阵分别记作 $F[i],M,F[i-1]$,即
$$
F[i] = M\times F[i-1]
$$
那么有
$$
\begin{aligned}
F[n] &= M\times F[n-1] \
&= M\times M\times F[n-2] \
&= M\times M\times M\times F[n-3] \
&\ \ \vdots \
&= M^{n-1}\times F[1] \
\end{aligned}
$$
其中 $M^{n-1}$ 可以用快速幂计算,原理请看【图解】一张图秒懂快速幂。
初始值
$$
F[1] = \begin{bmatrix}
f[1] \
f[0] \
\end{bmatrix}
= \begin{bmatrix}
12 \
3 \
\end{bmatrix}
$$
答案为 $f[n]$,即 $F[n]$ 的第一项。
###py
MOD = 1_000_000_007
# a @ b,其中 @ 是矩阵乘法
def mul(a: List[List[int]], b: List[List[int]]) -> List[List[int]]:
return [[sum(x * y for x, y in zip(row, col)) % MOD for col in zip(*b)]
for row in a]
# a^n @ f0
def pow_mul(a: List[List[int]], n: int, f0: List[List[int]]) -> List[List[int]]:
res = f0
while n:
if n & 1:
res = mul(a, res)
a = mul(a, a)
n >>= 1
return res
class Solution:
def numOfWays(self, n: int) -> int:
m = [[5, -2], [1, 0]]
f1 = [[12], [3]]
fn = pow_mul(m, n - 1, f1)
return fn[0][0]
###py
import numpy as np
class Solution:
def numOfWays(self, n: int) -> int:
MOD = 1_000_000_007
m = np.array([[5, -2], [1, 0]], dtype=object)
f1 = np.array([12, 3], dtype=object)
fn = np.linalg.matrix_power(m, n - 1) @ f1
return fn[0] % MOD
###java
class Solution {
private static final int MOD = 1_000_000_007;
public int numOfWays(int n) {
int[][] m = {
{5, -2},
{1, 0},
};
int[][] f1 = {{12}, {3}};
int[][] fn = powMul(m, n - 1, f1);
return (fn[0][0] + MOD) % MOD; // 保证结果非负
}
// a^n * f0
private int[][] powMul(int[][] a, int n, int[][] f0) {
int[][] res = f0;
while (n > 0) {
if ((n & 1) > 0) {
res = mul(a, res);
}
a = mul(a, a);
n >>= 1;
}
return res;
}
// 返回矩阵 a 和矩阵 b 相乘的结果
private int[][] mul(int[][] a, int[][] b) {
int[][] c = new int[a.length][b[0].length];
for (int i = 0; i < a.length; i++) {
for (int k = 0; k < a[i].length; k++) {
if (a[i][k] == 0) {
continue;
}
for (int j = 0; j < b[k].length; j++) {
c[i][j] = (int) ((c[i][j] + (long) a[i][k] * b[k][j]) % MOD);
}
}
}
return c;
}
}
###cpp
constexpr int MOD = 1'000'000'007;
using matrix = vector<vector<int>>;
// 返回矩阵 a 和矩阵 b 相乘的结果
matrix mul(matrix& a, matrix& b) {
int n = a.size(), m = b[0].size();
matrix c = matrix(n, vector<int>(m));
for (int i = 0; i < n; i++) {
for (int k = 0; k < a[i].size(); k++) {
if (a[i][k] == 0) {
continue;
}
for (int j = 0; j < m; j++) {
c[i][j] = (c[i][j] + 1LL * a[i][k] * b[k][j]) % MOD;
}
}
}
return c;
}
// a^n * f0
matrix pow_mul(matrix a, int n, matrix& f0) {
matrix res = f0;
while (n) {
if (n & 1) {
res = mul(a, res);
}
a = mul(a, a);
n >>= 1;
}
return res;
}
class Solution {
public:
int numOfWays(int n) {
matrix m = {
{5, -2},
{1, 0},
};
matrix f1 = {{12}, {3}};
matrix fn = pow_mul(m, n - 1, f1);
return (fn[0][0] + MOD) % MOD; // 保证结果非负
}
};
###go
const mod = 1_000_000_007
type matrix [][]int
func newMatrix(n, m int) matrix {
a := make(matrix, n)
for i := range a {
a[i] = make([]int, m)
}
return a
}
// 返回矩阵 a 和矩阵 b 相乘的结果
func (a matrix) mul(b matrix) matrix {
c := newMatrix(len(a), len(b[0]))
for i, row := range a {
for k, x := range row {
if x == 0 {
continue
}
for j, y := range b[k] {
c[i][j] = (c[i][j] + x*y) % mod
}
}
}
return c
}
// a^n * f0
func (a matrix) powMul(n int, f0 matrix) matrix {
res := f0
for ; n > 0; n /= 2 {
if n%2 > 0 {
res = a.mul(res)
}
a = a.mul(a)
}
return res
}
func numOfWays(n int) int {
m := matrix{
{5, -2},
{1, 0},
}
f1 := matrix{{12}, {3}}
fn := m.powMul(n-1, f1)
return (fn[0][0] + mod) % mod // 保证结果非负
}
复杂度分析
- 时间复杂度:$\mathcal{O}(\log n)$。
- 空间复杂度:$\mathcal{O}(1)$。
注:也可以用 Kitamasa 算法 计算,在矩阵更大(递推式更长)时有优势。
相似题目
- 1931. 用三种不同颜色为网格涂色 2170
- 1659. 最大化网格幸福感 2655
专题训练
见下面动态规划题单的「§9.5 轮廓线 DP」和「§11.6 矩阵快速幂优化 DP」。
分类题单
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 二分算法(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流)
- 动态规划(入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)
欢迎关注 B站@灵茶山艾府
给 N x 3 网格图涂色的方案数
方法一:递推
我们可以用 $f[i][\textit{type}]$ 表示当网格的大小为 $i \times 3$ 且最后一行的填色方法为 $\textit{type}$ 时的方案数。由于我们在填充第 $i$ 行时,会影响我们填充方案的只有它上面的那一行(即 $i - 1$ 行),因此用 $f[i][\textit{type}]$ 表示状态是合理的。
那么我们如何计算 $f[i][\textit{type}]$ 呢?可以发现:
-
首先,$\textit{type}$ 本身是要满足要求的。每一行有 $3$ 个网格,如果我们用 $0, 1, 2$ 分别代表红黄绿,那么 $\textit{type}$ 可以看成一个三进制数,例如 $\textit{type} = (102)_3$ 时,表示 $3$ 个网格从左到右的颜色分别为黄、红、绿;
- 这样以来,我们可以预处理出所有满足要求的 $\textit{type}$。具体地,我们使用三重循环分别枚举每一个格子的颜色,只有相邻的格子颜色不相同时,$\textit{type}$ 才满足要求。
-
其次,$f[i][\textit{type}]$ 应该等于所有 $f[i - 1][\textit{type}']$ 的和,其中 $\textit{type'}$ 和 $\textit{type}$ 可以作为相邻的行。也就是说,$\textit{type'}$ 和 $\textit{type}$ 的对应位置不能相同。
递推解法的本身不难想出,难度在于上述的预处理以及编码实现。下面给出包含详细注释的 C++、Java 和 Python 代码。
###C++
class Solution {
private:
static constexpr int mod = 1000000007;
public:
int numOfWays(int n) {
// 预处理出所有满足条件的 type
vector<int> types;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
for (int k = 0; k < 3; ++k) {
if (i != j && j != k) {
// 只要相邻的颜色不相同就行
// 将其以十进制的形式存储
types.push_back(i * 9 + j * 3 + k);
}
}
}
}
int type_cnt = types.size();
// 预处理出所有可以作为相邻行的 type 对
vector<vector<int>> related(type_cnt, vector<int>(type_cnt));
for (int i = 0; i < type_cnt; ++i) {
// 得到 types[i] 三个位置的颜色
int x1 = types[i] / 9, x2 = types[i] / 3 % 3, x3 = types[i] % 3;
for (int j = 0; j < type_cnt; ++j) {
// 得到 types[j] 三个位置的颜色
int y1 = types[j] / 9, y2 = types[j] / 3 % 3, y3 = types[j] % 3;
// 对应位置不同色,才能作为相邻的行
if (x1 != y1 && x2 != y2 && x3 != y3) {
related[i][j] = 1;
}
}
}
// 递推数组
vector<vector<int>> f(n + 1, vector<int>(type_cnt));
// 边界情况,第一行可以使用任何 type
for (int i = 0; i < type_cnt; ++i) {
f[1][i] = 1;
}
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < type_cnt; ++j) {
for (int k = 0; k < type_cnt; ++k) {
// f[i][j] 等于所有 f[i - 1][k] 的和
// 其中 k 和 j 可以作为相邻的行
if (related[k][j]) {
f[i][j] += f[i - 1][k];
f[i][j] %= mod;
}
}
}
}
// 最终所有的 f[n][...] 之和即为答案
int ans = 0;
for (int i = 0; i < type_cnt; ++i) {
ans += f[n][i];
ans %= mod;
}
return ans;
}
};
###Java
class Solution {
static final int MOD = 1000000007;
public int numOfWays(int n) {
// 预处理出所有满足条件的 type
List<Integer> types = new ArrayList<Integer>();
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
for (int k = 0; k < 3; ++k) {
if (i != j && j != k) {
// 只要相邻的颜色不相同就行
// 将其以十进制的形式存储
types.add(i * 9 + j * 3 + k);
}
}
}
}
int typeCnt = types.size();
// 预处理出所有可以作为相邻行的 type 对
int[][] related = new int[typeCnt][typeCnt];
for (int i = 0; i < typeCnt; ++i) {
// 得到 types[i] 三个位置的颜色
int x1 = types.get(i) / 9, x2 = types.get(i) / 3 % 3, x3 = types.get(i) % 3;
for (int j = 0; j < typeCnt; ++j) {
// 得到 types[j] 三个位置的颜色
int y1 = types.get(j) / 9, y2 = types.get(j) / 3 % 3, y3 = types.get(j) % 3;
// 对应位置不同色,才能作为相邻的行
if (x1 != y1 && x2 != y2 && x3 != y3) {
related[i][j] = 1;
}
}
}
// 递推数组
int[][] f = new int[n + 1][typeCnt];
// 边界情况,第一行可以使用任何 type
for (int i = 0; i < typeCnt; ++i) {
f[1][i] = 1;
}
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < typeCnt; ++j) {
for (int k = 0; k < typeCnt; ++k) {
// f[i][j] 等于所有 f[i - 1][k] 的和
// 其中 k 和 j 可以作为相邻的行
if (related[k][j] != 0) {
f[i][j] += f[i - 1][k];
f[i][j] %= MOD;
}
}
}
}
// 最终所有的 f[n][...] 之和即为答案
int ans = 0;
for (int i = 0; i < typeCnt; ++i) {
ans += f[n][i];
ans %= MOD;
}
return ans;
}
}
###Python
class Solution:
def numOfWays(self, n: int) -> int:
mod = 10**9 + 7
# 预处理出所有满足条件的 type
types = list()
for i in range(3):
for j in range(3):
for k in range(3):
if i != j and j != k:
# 只要相邻的颜色不相同就行
# 将其以十进制的形式存储
types.append(i * 9 + j * 3 + k)
type_cnt = len(types)
# 预处理出所有可以作为相邻行的 type 对
related = [[0] * type_cnt for _ in range(type_cnt)]
for i, ti in enumerate(types):
# 得到 types[i] 三个位置的颜色
x1, x2, x3 = ti // 9, ti // 3 % 3, ti % 3
for j, tj in enumerate(types):
# 得到 types[j] 三个位置的颜色
y1, y2, y3 = tj // 9, tj // 3 % 3, tj % 3
# 对应位置不同色,才能作为相邻的行
if x1 != y1 and x2 != y2 and x3 != y3:
related[i][j] = 1
# 递推数组
f = [[0] * type_cnt for _ in range(n + 1)]
# 边界情况,第一行可以使用任何 type
f[1] = [1] * type_cnt
for i in range(2, n + 1):
for j in range(type_cnt):
for k in range(type_cnt):
# f[i][j] 等于所有 f[i - 1][k] 的和
# 其中 k 和 j 可以作为相邻的行
if related[k][j]:
f[i][j] += f[i - 1][k]
f[i][j] %= mod
# 最终所有的 f[n][...] 之和即为答案
ans = sum(f[n]) % mod
return ans
###C#
public class Solution {
private const int mod = 1000000007;
public int NumOfWays(int n) {
// 预处理出所有满足条件的 type
List<int> types = new List<int>();
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
for (int k = 0; k < 3; ++k) {
if (i != j && j != k) {
// 只要相邻的颜色不相同就行
// 将其以十进制的形式存储
types.Add(i * 9 + j * 3 + k);
}
}
}
}
int type_cnt = types.Count;
// 预处理出所有可以作为相邻行的 type 对
int[][] related = new int[type_cnt][];
for (int i = 0; i < type_cnt; ++i) {
related[i] = new int[type_cnt];
// 得到 types[i] 三个位置的颜色
int x1 = types[i] / 9, x2 = types[i] / 3 % 3, x3 = types[i] % 3;
for (int j = 0; j < type_cnt; ++j) {
// 得到 types[j] 三个位置的颜色
int y1 = types[j] / 9, y2 = types[j] / 3 % 3, y3 = types[j] % 3;
// 对应位置不同色,才能作为相邻的行
if (x1 != y1 && x2 != y2 && x3 != y3) {
related[i][j] = 1;
}
}
}
// 递推数组
int[][] f = new int[n + 1][];
for (int i = 0; i <= n; ++i) {
f[i] = new int[type_cnt];
}
// 边界情况,第一行可以使用任何 type
for (int i = 0; i < type_cnt; ++i) {
f[1][i] = 1;
}
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < type_cnt; ++j) {
for (int k = 0; k < type_cnt; ++k) {
// f[i][j] 等于所有 f[i - 1][k] 的和
// 其中 k 和 j 可以作为相邻的行
if (related[k][j] == 1) {
f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
}
}
}
}
// 最终所有的 f[n][...] 之和即为答案
int ans = 0;
for (int i = 0; i < type_cnt; ++i) {
ans = (ans + f[n][i]) % mod;
}
return ans;
}
}
###Go
func numOfWays(n int) int {
// 预处理出所有满足条件的 type
mod := 1000000007
types := []int{}
for i := 0; i < 3; i++ {
for j := 0; j < 3; j++ {
for k := 0; k < 3; k++ {
if i != j && j != k {
// 只要相邻的颜色不相同就行
// 将其以十进制的形式存储
types = append(types, i*9 + j*3 + k)
}
}
}
}
type_cnt := len(types)
// 预处理出所有可以作为相邻行的 type 对
related := make([][]int, type_cnt)
for i := range related {
related[i] = make([]int, type_cnt)
}
for i := 0; i < type_cnt; i++ {
// 得到 types[i] 三个位置的颜色
x1 := types[i] / 9
x2 := types[i] / 3 % 3
x3 := types[i] % 3
for j := 0; j < type_cnt; j++ {
// 得到 types[j] 三个位置的颜色
y1 := types[j] / 9
y2 := types[j] / 3 % 3
y3 := types[j] % 3
// 对应位置不同色,才能作为相邻的行
if x1 != y1 && x2 != y2 && x3 != y3 {
related[i][j] = 1
}
}
}
// 递推数组
f := make([][]int, n+1)
for i := range f {
f[i] = make([]int, type_cnt)
}
// 边界情况,第一行可以使用任何 type
for i := 0; i < type_cnt; i++ {
f[1][i] = 1
}
for i := 2; i <= n; i++ {
for j := 0; j < type_cnt; j++ {
for k := 0; k < type_cnt; k++ {
// f[i][j] 等于所有 f[i - 1][k] 的和
// 其中 k 和 j 可以作为相邻的行
if related[k][j] == 1 {
f[i][j] = (f[i][j] + f[i-1][k]) % mod
}
}
}
}
// 最终所有的 f[n][...] 之和即为答案
ans := 0
for i := 0; i < type_cnt; i++ {
ans = (ans + f[n][i]) % mod
}
return ans
}
###C
int numOfWays(int n) {
// 预处理出所有满足条件的 type
const int mod = 1000000007;
int types[12];
int type_cnt = 0;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
for (int k = 0; k < 3; ++k) {
if (i != j && j != k) {
// 只要相邻的颜色不相同就行
// 将其以十进制的形式存储
types[type_cnt++] = i * 9 + j * 3 + k;
}
}
}
}
// 预处理出所有可以作为相邻行的 type 对
int related[12][12] = {0};
for (int i = 0; i < type_cnt; ++i) {
// 得到 types[i] 三个位置的颜色
int x1 = types[i] / 9, x2 = types[i] / 3 % 3, x3 = types[i] % 3;
for (int j = 0; j < type_cnt; ++j) {
// 得到 types[j] 三个位置的颜色
int y1 = types[j] / 9, y2 = types[j] / 3 % 3, y3 = types[j] % 3;
// 对应位置不同色,才能作为相邻的行
if (x1 != y1 && x2 != y2 && x3 != y3) {
related[i][j] = 1;
}
}
}
// 递推数组
int f[n + 1][type_cnt];
// 初始化
for (int i = 0; i <= n; ++i) {
for (int j = 0; j < type_cnt; ++j) {
f[i][j] = 0;
}
}
// 边界情况,第一行可以使用任何 type
for (int i = 0; i < type_cnt; ++i) {
f[1][i] = 1;
}
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < type_cnt; ++j) {
for (int k = 0; k < type_cnt; ++k) {
// f[i][j] 等于所有 f[i - 1][k] 的和
// 其中 k 和 j 可以作为相邻的行
if (related[k][j]) {
f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
}
}
}
}
// 最终所有的 f[n][...] 之和即为答案
int ans = 0;
for (int i = 0; i < type_cnt; ++i) {
ans = (ans + f[n][i]) % mod;
}
return ans;
}
###JavaScript
var numOfWays = function(n) {
// 预处理出所有满足条件的 type
const mod = 1000000007;
const types = [];
for (let i = 0; i < 3; ++i) {
for (let j = 0; j < 3; ++j) {
for (let k = 0; k < 3; ++k) {
if (i !== j && j !== k) {
// 只要相邻的颜色不相同就行
// 将其以十进制的形式存储
types.push(i * 9 + j * 3 + k);
}
}
}
}
const type_cnt = types.length;
// 预处理出所有可以作为相邻行的 type 对
const related = Array.from({length: type_cnt}, () => new Array(type_cnt).fill(0));
for (let i = 0; i < type_cnt; ++i) {
// 得到 types[i] 三个位置的颜色
const x1 = Math.floor(types[i] / 9);
const x2 = Math.floor(types[i] / 3) % 3;
const x3 = types[i] % 3;
for (let j = 0; j < type_cnt; ++j) {
// 得到 types[j] 三个位置的颜色
const y1 = Math.floor(types[j] / 9);
const y2 = Math.floor(types[j] / 3) % 3;
const y3 = types[j] % 3;
// 对应位置不同色,才能作为相邻的行
if (x1 !== y1 && x2 !== y2 && x3 !== y3) {
related[i][j] = 1;
}
}
}
// 递推数组
const f = Array.from({length: n + 1}, () => new Array(type_cnt).fill(0));
// 边界情况,第一行可以使用任何 type
for (let i = 0; i < type_cnt; ++i) {
f[1][i] = 1;
}
for (let i = 2; i <= n; ++i) {
for (let j = 0; j < type_cnt; ++j) {
for (let k = 0; k < type_cnt; ++k) {
// f[i][j] 等于所有 f[i - 1][k] 的和
// 其中 k 和 j 可以作为相邻的行
if (related[k][j]) {
f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
}
}
}
}
// 最终所有的 f[n][...] 之和即为答案
let ans = 0;
for (let i = 0; i < type_cnt; ++i) {
ans = (ans + f[n][i]) % mod;
}
return ans;
};
###TypeScript
function numOfWays(n: number): number {
// 预处理出所有满足条件的 type
const mod: number = 1000000007;
const types: number[] = [];
for (let i = 0; i < 3; ++i) {
for (let j = 0; j < 3; ++j) {
for (let k = 0; k < 3; ++k) {
if (i !== j && j !== k) {
// 只要相邻的颜色不相同就行
// 将其以十进制的形式存储
types.push(i * 9 + j * 3 + k);
}
}
}
}
const type_cnt: number = types.length;
// 预处理出所有可以作为相邻行的 type 对
const related: number[][] = Array.from({length: type_cnt}, () => new Array(type_cnt).fill(0));
for (let i = 0; i < type_cnt; ++i) {
// 得到 types[i] 三个位置的颜色
const x1: number = Math.floor(types[i] / 9);
const x2: number = Math.floor(types[i] / 3) % 3;
const x3: number = types[i] % 3;
for (let j = 0; j < type_cnt; ++j) {
// 得到 types[j] 三个位置的颜色
const y1: number = Math.floor(types[j] / 9);
const y2: number = Math.floor(types[j] / 3) % 3;
const y3: number = types[j] % 3;
// 对应位置不同色,才能作为相邻的行
if (x1 !== y1 && x2 !== y2 && x3 !== y3) {
related[i][j] = 1;
}
}
}
// 递推数组
const f: number[][] = Array.from({length: n + 1}, () => new Array(type_cnt).fill(0));
// 边界情况,第一行可以使用任何 type
for (let i = 0; i < type_cnt; ++i) {
f[1][i] = 1;
}
for (let i = 2; i <= n; ++i) {
for (let j = 0; j < type_cnt; ++j) {
for (let k = 0; k < type_cnt; ++k) {
// f[i][j] 等于所有 f[i - 1][k] 的和
// 其中 k 和 j 可以作为相邻的行
if (related[k][j]) {
f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
}
}
}
}
// 最终所有的 f[n][...] 之和即为答案
let ans: number = 0;
for (let i = 0; i < type_cnt; ++i) {
ans = (ans + f[n][i]) % mod;
}
return ans;
}
###Rust
impl Solution {
pub fn num_of_ways(n: i32) -> i32 {
// 预处理出所有满足条件的 type
let mod_val = 1000000007;
let n = n as usize;
let mut types = Vec::new();
for i in 0..3 {
for j in 0..3 {
for k in 0..3 {
if i != j && j != k {
// 只要相邻的颜色不相同就行
// 将其以十进制的形式存储
types.push(i * 9 + j * 3 + k);
}
}
}
}
let type_cnt = types.len();
// 预处理出所有可以作为相邻行的 type 对
let mut related = vec![vec![0; type_cnt]; type_cnt];
for i in 0..type_cnt {
// 得到 types[i] 三个位置的颜色
let x1 = types[i] / 9;
let x2 = types[i] / 3 % 3;
let x3 = types[i] % 3;
for j in 0..type_cnt {
// 得到 types[j] 三个位置的颜色
let y1 = types[j] / 9;
let y2 = types[j] / 3 % 3;
let y3 = types[j] % 3;
// 对应位置不同色,才能作为相邻的行
if x1 != y1 && x2 != y2 && x3 != y3 {
related[i][j] = 1;
}
}
}
// 递推数组
let mut f = vec![vec![0; type_cnt]; n + 1];
// 边界情况,第一行可以使用任何 type
for i in 0..type_cnt {
f[1][i] = 1;
}
for i in 2..=n {
for j in 0..type_cnt {
for k in 0..type_cnt {
// f[i][j] 等于所有 f[i - 1][k] 的和
// 其中 k 和 j 可以作为相邻的行
if related[k][j] == 1 {
f[i][j] = (f[i][j] + f[i - 1][k]) % mod_val;
}
}
}
}
// 最终所有的 f[n][...] 之和即为答案
let mut ans = 0;
for i in 0..type_cnt {
ans = (ans + f[n][i]) % mod_val;
}
ans
}
}
复杂度分析
-
时间复杂度:$O(T^2N)$,其中 $T$ 是满足要求的 $\textit{type}$ 的数量,在示例一中已经给出了 $T = 12$。在递推的过程中,我们需要计算所有的 $f[i][\textit{type}]$,并且需要枚举上一行的 $\textit{type}'$。
-
空间复杂度:$O(T^2 + TN)$。我们需要 $T * T$ 的二维数组存储 $\textit{type}$ 之间的关系,$T * N$ 的数组存储递推的结果。注意到由于 $f[i][\textit{type}]$ 只和上一行的状态有关,我们可以使用两个一维数组存储当前行和上一行的 $f$ 值,空间复杂度降低至 $O(T^2 + 2T) = O(T^2)$。
方法二:递推优化
如果读者有一些高中数学竞赛基础,就可以发现上面的这个递推式是线性的,也就是说:
-
我们可以进行一些化简;
-
它存在通项公式。
直观上,我们怎么化简方法一中的递推呢?
我们把满足要求的 $\textit{type}$ 都写出来,一共有 $12$ 种:
010, 012, 020, 021, 101, 102, 120, 121, 201, 202, 210, 212
我们可以把它们分成两类:
-
ABC类:三个颜色互不相同,一共有 $6$ 种:012, 021, 102, 120, 201, 210; -
ABA类:左右两侧的颜色相同,也有 $6$ 种:010, 020, 101, 121, 202, 212。
这样我们就可以把 $12$ 种 $\textit{type}$ 浓缩成了 $2$ 种,尝试写出这两类之间的递推式。我们用 $f[i][0]$ 表示 ABC 类,$f[i][1]$ 表示 ABA 类。在计算时,我们可以将任意一种满足要求的涂色方法带入第 i - 1 行,并检查第 i 行的方案数,这是因为同一类的涂色方法都是等价的:
-
第
i - 1行是ABC类,第i行是ABC类:以012为例,那么第i行只能是120或201,方案数为 $2$; -
第
i - 1行是ABC类,第i行是ABA类:以012为例,那么第i行只能是101或121,方案数为 $2$; -
第
i - 1行是ABA类,第i行是ABC类:以010为例,那么第i行只能是102或201,方案数为2; -
第
i - 1行是ABA类,第i行是ABA类:以010为例,那么第i行只能是101,121或202,方案数为3。
因此我们就可以写出递推式:
$$
\begin{cases}
f[i][0] = 2 * f[i - 1][0] + 2 * f[i - 1][1] \
f[i][1] = 2 * f[i - 1][0] + 3 * f[i - 1][1]
\end{cases}
$$
###C++
class Solution {
private:
static constexpr int mod = 1000000007;
public:
int numOfWays(int n) {
int fi0 = 6, fi1 = 6;
for (int i = 2; i <= n; ++i) {
int new_fi0 = (2LL * fi0 + 2LL * fi1) % mod;
int new_fi1 = (2LL * fi0 + 3LL * fi1) % mod;
fi0 = new_fi0;
fi1 = new_fi1;
}
return (fi0 + fi1) % mod;
}
};
###Java
class Solution {
static final int MOD = 1000000007;
public int numOfWays(int n) {
long fi0 = 6, fi1 = 6;
for (int i = 2; i <= n; ++i) {
long newFi0 = (2 * fi0 + 2 * fi1) % MOD;
long newFi1 = (2 * fi0 + 3 * fi1) % MOD;
fi0 = newFi0;
fi1 = newFi1;
}
return (int) ((fi0 + fi1) % MOD);
}
}
###Python
class Solution:
def numOfWays(self, n: int) -> int:
mod = 10**9 + 7
fi0, fi1 = 6, 6
for i in range(2, n + 1):
fi0, fi1 = (2 * fi0 + 2 * fi1) % mod, (2 * fi0 + 3 * fi1) % mod
return (fi0 + fi1) % mod
###C#
public class Solution {
private const int mod = 1000000007;
public int NumOfWays(int n) {
long fi0 = 6, fi1 = 6;
for (int i = 2; i <= n; ++i) {
long new_fi0 = (2 * fi0 + 2 * fi1) % mod;
long new_fi1 = (2 * fi0 + 3 * fi1) % mod;
fi0 = new_fi0;
fi1 = new_fi1;
}
return (int)((fi0 + fi1) % mod);
}
}
###Go
func numOfWays(n int) int {
mod := 1000000007
fi0, fi1 := 6, 6
for i := 2; i <= n; i++ {
new_fi0 := (2*fi0 + 2*fi1) % mod
new_fi1 := (2*fi0 + 3*fi1) % mod
fi0, fi1 = new_fi0, new_fi1
}
return (fi0 + fi1) % mod
}
###C
int numOfWays(int n) {
const int mod = 1000000007;
long long fi0 = 6, fi1 = 6;
for (int i = 2; i <= n; ++i) {
long long new_fi0 = (2 * fi0 + 2 * fi1) % mod;
long long new_fi1 = (2 * fi0 + 3 * fi1) % mod;
fi0 = new_fi0;
fi1 = new_fi1;
}
return (fi0 + fi1) % mod;
}
###JavaScript
var numOfWays = function(n) {
const mod = 1000000007;
let fi0 = 6, fi1 = 6;
for (let i = 2; i <= n; i++) {
const new_fi0 = (2 * fi0 + 2 * fi1) % mod;
const new_fi1 = (2 * fi0 + 3 * fi1) % mod;
fi0 = new_fi0;
fi1 = new_fi1;
}
return (fi0 + fi1) % mod;
};
###TypeScript
function numOfWays(n: number): number {
const mod: number = 1000000007;
let fi0: number = 6, fi1: number = 6;
for (let i = 2; i <= n; i++) {
const new_fi0: number = (2 * fi0 + 2 * fi1) % mod;
const new_fi1: number = (2 * fi0 + 3 * fi1) % mod;
fi0 = new_fi0;
fi1 = new_fi1;
}
return (fi0 + fi1) % mod;
}
###Rust
impl Solution {
pub fn num_of_ways(n: i32) -> i32 {
let mod_val: i64 = 1000000007;
let mut fi0: i64 = 6;
let mut fi1: i64 = 6;
for _ in 2..= n {
let new_fi0 = (2 * fi0 + 2 * fi1) % mod_val;
let new_fi1 = (2 * fi0 + 3 * fi1) % mod_val;
fi0 = new_fi0;
fi1 = new_fi1;
}
((fi0 + fi1) % mod_val) as i32
}
}
复杂度分析
-
时间复杂度:$O(N)$。
-
空间复杂度:$O(1)$。
数学解决非常快乐
1.观察LEETCODE给的官方N=1示例,可以抽象区分为2种类型,ABA和ABC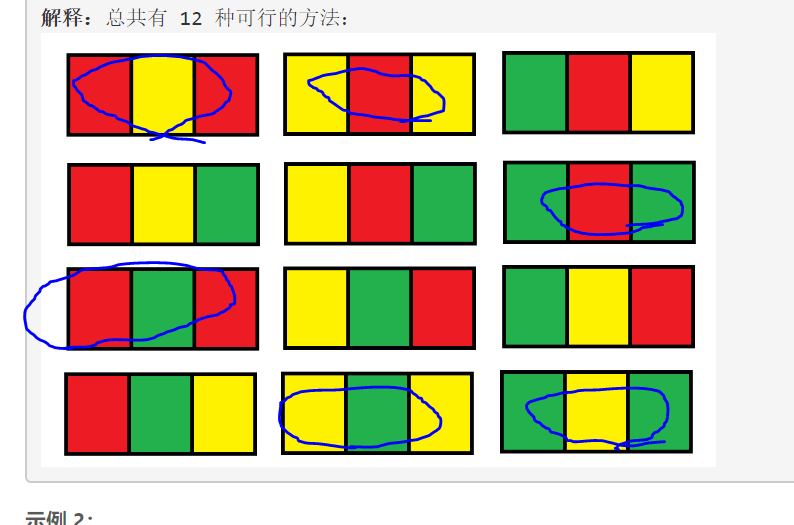
2.分情况讨论,可知,在下方增加1行时,有9种情况,又可以分为ABA和ABC两个大类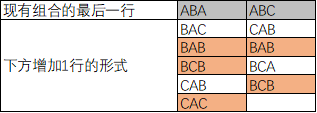
本层的结果 = ABA类的个数m + ABC类的个数n
本层的每个ABA类 => 下层演化 3个ABA + 2个ABC
本层的每个ABC类 => 下层演化 2个ABA + 2个ABC
下层的结果 = ABA类的个数 + ABC类的个数 = (3m+2n) + (2m+2n)
3.数学计算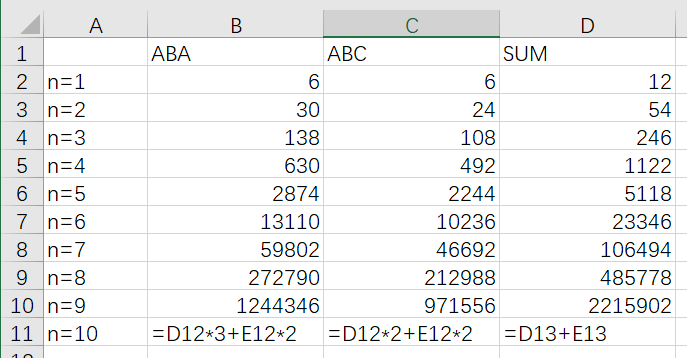
4.最后给出代码
###csharp
public class Solution {
public int NumOfWays(int n) {
if (n == 0)
return 0;
else if (n == 1)
return 12;
var temp = 1000000007;
long repeat = 6;
long unrepeat = 6;
for(int i = 2; i <=n; i++)
{
long newrep = (repeat * 3) % temp + unrepeat * 2 % temp;
long newunrep = repeat * 2 % temp + unrepeat * 2 % temp;
repeat = newrep;
unrepeat = newunrep;
}
return (int)((repeat + unrepeat)%temp);
}
}