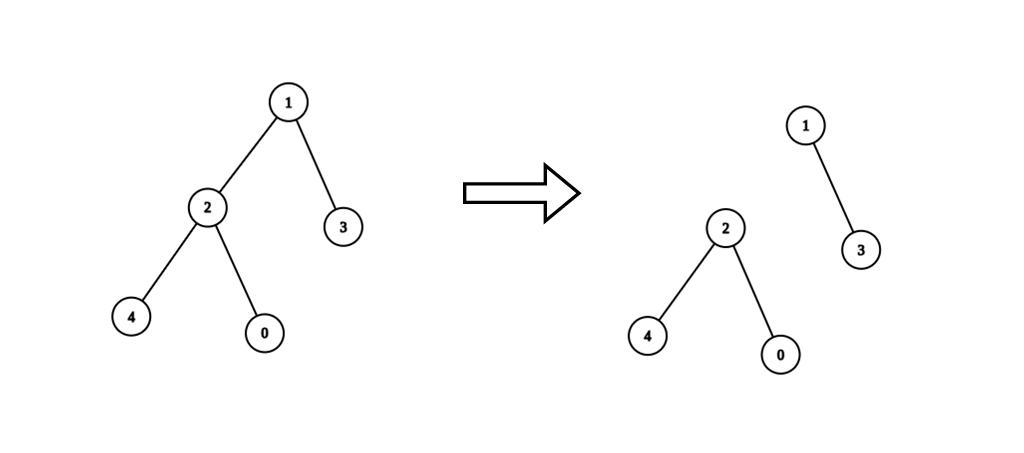
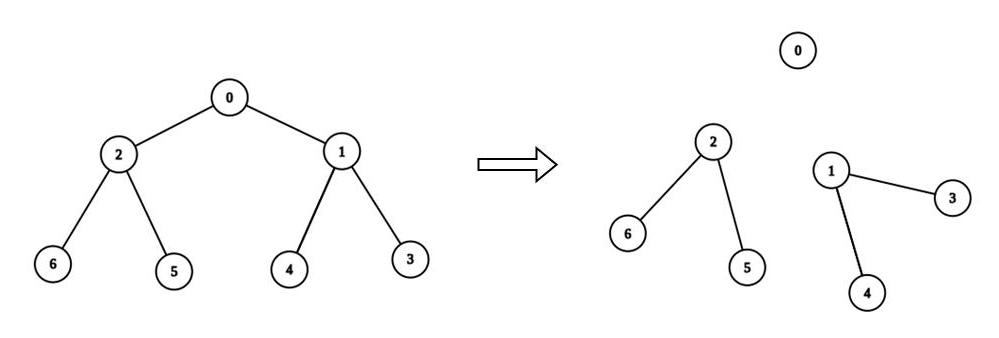
最大化连通块的数目,等价于最大化删除的边数加一。
什么样的边可以删除?
如果 $x$ 和 $y$ 都是 $k$ 的倍数,那么 $x+y$ 也是 $k$ 的倍数。比如 $3$ 和 $6$ 都是 $3$ 的倍数,那么 $3+6=9$ 也是 $3$ 的倍数。
反过来说(逆否命题),如果 $x+y$ 不是 $k$ 的倍数,那么 $x$ 和 $y$ 不全是 $k$ 的倍数。不是 $k$ 的倍数的数,继续拆分,始终存在一个不是 $k$ 的倍数的数。
对应到删边上,删除一条边后,我们把一个连通块分成了两个连通块。如果其中一个连通块的点权和不是 $k$ 的倍数,那么这个连通块无论如何分割,始终存在一个点权和不是 $k$ 的倍数的连通块。所以当且仅当这两个连通块的点权和都是 $k$ 的倍数,这条边才能删除。
删除后,由于分割出的连通块点权和仍然是 $k$ 的倍数,所以可以继续分割,直到无法分割为止。换句话说,只要有能删除的边,就删除。
如何找到可以删除的边?
删除一条边后,我们把一个连通块分成了两个连通块。由于题目保证整棵树的点权和是 $k$ 的倍数,所以只需看其中一个连通块的点权和是否为 $k$ 的倍数。
从任意点出发 DFS 这棵树。计算子树 $x$ 的点权和 $s$,如果 $s$ 是 $k$ 的倍数,那么可以删除 $x$ 到其父节点这条边。注意根节点没有父节点。
连通块的数目等于删除的边数加一。可以把根节点到其父节点这条边(虽然不存在)也算上,这样答案就是删除的边数。
class Solution:
def maxKDivisibleComponents(self, n: int, edges: List[List[int]], values: List[int], k: int) -> int:
g = [[] for _ in range(n)]
for x, y in edges:
g[x].append(y)
g[y].append(x)
# 返回子树 x 的点权和
def dfs(x: int, fa: int) -> int:
s = values[x]
for y in g[x]:
if y != fa: # 避免访问父节点
# 加上子树 y 的点权和,得到子树 x 的点权和
s += dfs(y, x)
nonlocal ans
ans += s % k == 0
return s
ans = 0
dfs(0, -1)
return ans
class Solution {
private int ans;
public int maxKDivisibleComponents(int n, int[][] edges, int[] values, int k) {
List<Integer>[] g = new ArrayList[n];
Arrays.setAll(g, _ -> new ArrayList<>());
for (int[] e : edges) {
int x = e[0];
int y = e[1];
g[x].add(y);
g[y].add(x);
}
dfs(0, -1, g, values, k);
return ans;
}
// 返回子树 x 的点权和
private long dfs(int x, int fa, List<Integer>[] g, int[] values, int k) {
long sum = values[x];
for (int y : g[x]) {
if (y != fa) { // 避免访问父节点
// 加上子树 y 的点权和,得到子树 x 的点权和
sum += dfs(y, x, g, values, k);
}
}
ans += sum % k == 0 ? 1 : 0;
return sum;
}
}
class Solution {
public:
int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {
vector<vector<int>> g(n);
for (auto& e : edges) {
int x = e[0], y = e[1];
g[x].push_back(y);
g[y].push_back(x);
}
int ans = 0;
// 返回子树 x 的点权和
auto dfs = [&](this auto&& dfs, int x, int fa) -> long long {
long long sum = values[x];
for (int y : g[x]) {
if (y != fa) { // 避免访问父节点
// 加上子树 y 的点权和,得到子树 x 的点权和
sum += dfs(y, x);
}
}
ans += sum % k == 0;
return sum;
};
dfs(0, -1);
return ans;
}
};
func maxKDivisibleComponents(n int, edges [][]int, values []int, k int) (ans int) {
g := make([][]int, n)
for _, e := range edges {
x, y := e[0], e[1]
g[x] = append(g[x], y)
g[y] = append(g[y], x)
}
// 返回子树 x 的点权和
var dfs func(int, int) int
dfs = func(x, fa int) int {
s := values[x]
for _, y := range g[x] {
if y != fa { // 避免访问父节点
// 加上子树 y 的点权和,得到子树 x 的点权和
s += dfs(y, x)
}
}
if s%k == 0 {
ans++
}
return s
}
dfs(0, -1)
return
}
var maxKDivisibleComponents = function(n, edges, values, k) {
const g = Array.from({ length: n }, () => []);
for (const [x, y] of edges) {
g[x].push(y);
g[y].push(x);
}
let ans = 0;
// 返回子树 x 的点权和
function dfs(x, fa) {
let sum = values[x];
for (const y of g[x]) {
if (y !== fa) { // 避免访问父节点
// 加上子树 y 的点权和,得到子树 x 的点权和
sum += dfs(y, x);
}
}
ans += sum % k === 0 ? 1 : 0;
return sum;
}
dfs(0, -1);
return ans;
};
impl Solution {
pub fn max_k_divisible_components(n: i32, edges: Vec<Vec<i32>>, values: Vec<i32>, k: i32) -> i32 {
let n = n as usize;
let mut g = vec![vec![]; n];
for e in edges {
let x = e[0] as usize;
let y = e[1] as usize;
g[x].push(y);
g[y].push(x);
}
// 返回子树 x 的点权和
fn dfs(x: usize, fa: usize, g: &[Vec<usize>], values: &[i32], k: i64, ans: &mut i32) -> i64 {
let mut sum = values[x] as i64;
for &y in &g[x] {
if y != fa { // 避免访问父节点
// 加上子树 y 的点权和,得到子树 x 的点权和
sum += dfs(y, x, g, values, k, ans);
}
}
if sum % k == 0 {
*ans += 1;
}
sum
}
let mut ans = 0;
dfs(0, 0, &g, &values, k as i64, &mut ans);
ans
}
}
复杂度分析
- 时间复杂度:$\mathcal{O}(n)$。
- 空间复杂度:$\mathcal{O}(n)$。
相似题目
2440. 创建价值相同的连通块
分类题单
如何科学刷题?
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 二分算法(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流)
- 动态规划(入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)
我的题解精选(已分类)
欢迎关注 B站@灵茶山艾府