Web开发中的文件下载

掘金前端

前端小巷子

2025年7月8日 08:28

在Web开发中，文件下载是一个常见的功能需求。实现文件下载功能都需要开发者对HTTP协议和浏览器行为有一定的了解。本文将详细介绍文件下载的消息格式、如何触发浏览器下载行为。

PWA渐进式Web应用技术深度解析

掘金前端

一拳不是超人

2025年7月8日 08:18

渐进式Web应用（Progressive Web App）是一种使用现代Web技术构建的应用程序，它结合了Web应用的广泛覆盖性和原生应用的优秀体验

每日一题-最多可以参加的会议数目 II🔴

LeetCode 每日一题题解

2025年7月8日 00:00

给你一个 events 数组，其中 events[i] = [startDay_i, endDay_i, value_i] ，表示第 i 个会议在 startDay_i天开始，第 endDay_i 天结束，如果你参加这个会议，你能得到价值 value_i 。同时给你一个整数 k 表示你能参加的最多会议数目。

你同一时间只能参加一个会议。如果你选择参加某个会议，那么你必须完整地参加完这个会议。会议结束日期是包含在会议内的，也就是说你不能同时参加一个开始日期与另一个结束日期相同的两个会议。

请你返回能得到的会议价值 最大和 。

示例 1：

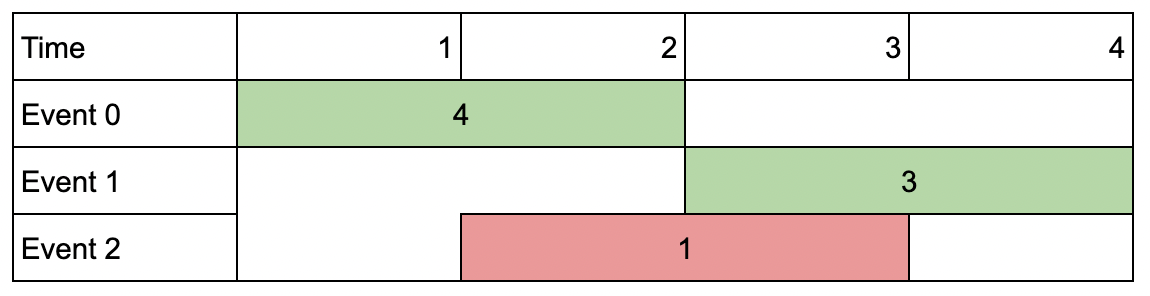
输入：events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
输出：7
解释：选择绿色的活动会议 0 和 1，得到总价值和为 4 + 3 = 7 。

示例 2：

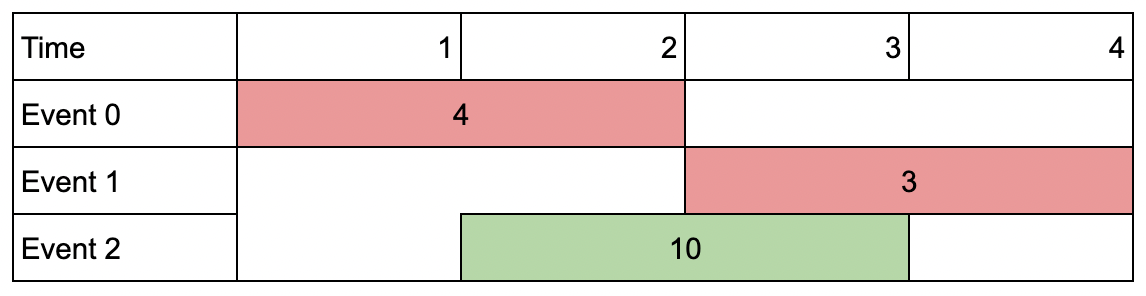
输入：events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
输出：10
解释：参加会议 2 ，得到价值和为 10 。
你没法再参加别的会议了，因为跟会议 2 有重叠。你 不 需要参加满 k 个会议。

示例 3：

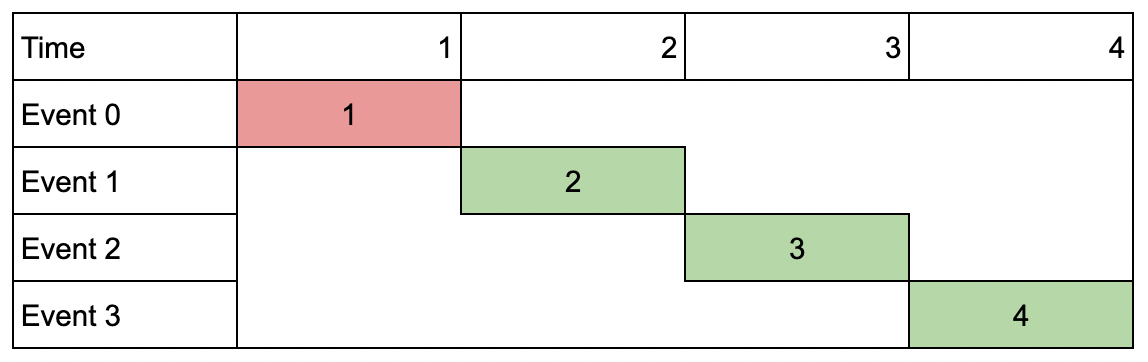
输入：events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
输出：9
解释：尽管会议互不重叠，你只能参加 3 个会议，所以选择价值最大的 3 个会议。

提示：

1 <= k <= events.length
1 <= k * events.length <= 10⁶
1 <= startDay_i <= endDay_i <= 10⁹
1 <= value_i <= 10⁶

动态规划 + 二分查找优化（Python/Java/C++/Go/JS/Rust）

LeetCode 每日一题题解

endlesscheng

2022年10月22日 07:35

请先完成本题的简单版本：1235. 规划兼职工作，我的题解。

本题在 1235 的基础上，约束参加的会议个数至多为 $k$。相应地，DP 要增加一个参数 $j$，表示至多参加 $j$ 个会议。

和 1235 一样，按照结束时间排序。定义 $f[i+1][j]$ 表示参加 $\textit{events}[0]$ 到 $\textit{events}[i]$ 中的至多 $j$ 个会议，能得到的最大价值和。其中 $+1$ 是为了方便用 $f[0]$ 表示初始值，即没有会议的情况。

分类讨论：

不参加 $\textit{events}[i]$，问题变成参加 $\textit{events}[0]$ 到 $\textit{events}[i-1]$ 中的至多 $j$ 个会议，能得到的最大价值和，即 $f[i][j]$；
参加 $\textit{events}[i]$，设 $p$ 是最大的满足 $\textit{endDay}_p<\textit{startDay}_i$ 的 $p$（若不存在则 $p=-1$），问题变成参加 $\textit{events}[0]$ 到 $\textit{events}[p]$ 中的至多 $j-1$ 个会议，能得到的会议价值的最大和，即 $f[p+1][j-1] + \textit{value}_i$。

两种情况取最大值，得到状态转移方程：

$$
f[i+1][j] = \max(f[i][j], f[p+1][j-1] + \textit{value}_i)
$$

由于结束时间是有序的（我们排过序了），$p$ 可以用二分查找快速计算，原理见二分查找红蓝染色法【基础算法精讲 04】。

初始值：$f[0][j] = 0$。没有会议，价值和为 $0$。

答案：$f[n][k]$。

# 手写 max 更快
max = lambda a, b: b if b > a else a

class Solution:
    def maxValue(self, events: List[List[int]], k: int) -> int:
        events.sort(key=lambda e: e[1])  # 按照结束时间排序
        n = len(events)
        f = [[0] * (k + 1) for _ in range(n + 1)]
        for i, (start_day, _, value) in enumerate(events):
            p = bisect_left(events, start_day, hi=i, key=lambda e: e[1])  # hi=i 表示二分上界为 i（默认为 n）
            for j in range(1, k + 1):
                # 为什么是 p 不是 p+1：上面算的是 >= start_day，-1 后得到 < start_day，但由于还要 +1，抵消了
                f[i + 1][j] = max(f[i][j], f[p][j - 1] + value)
        return f[n][k]

class Solution {
    public int maxValue(int[][] events, int k) {
        Arrays.sort(events, (a, b) -> a[1] - b[1]); // 按照结束时间排序
        int n = events.length;
        int[][] f = new int[n + 1][k + 1];
        for (int i = 0; i < n; i++) {
            int p = search(events, i, events[i][0]);
            for (int j = 1; j <= k; j++) {
                f[i + 1][j] = Math.max(f[i][j], f[p + 1][j - 1] + events[i][2]);
            }
        }
        return f[n][k];
    }

    // 返回 endDay[i] < upper 的最大 i
    private int search(int[][] events, int right, int upper) {
        int left = -1;
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;
            if (events[mid][1] < upper) {
                left = mid;
            } else {
                right = mid;
            }
        }
        return left;
    }
}

class Solution {
public:
    int maxValue(vector<vector<int>>& events, int k) {
        ranges::sort(events, {}, [](auto& e) { return e[1]; }); // 按照结束时间排序
        int n = events.size();
        vector f(n + 1, vector<int>(k + 1));
        for (int i = 0; i < n; i++) {
            int p = lower_bound(events.begin(), events.begin() + i, events[i][0],
                                [](auto& e, int lower) { return e[1] < lower; }) - events.begin();
            for (int j = 1; j <= k; j++) {
                // 为什么是 p 不是 p+1：上面算的是 >= startDay，-1 后得到 < startDay，但由于还要 +1，抵消了
                f[i + 1][j] = max(f[i][j], f[p][j - 1] + events[i][2]);
            }
        }
        return f[n][k];
    }
};

func maxValue(events [][]int, k int) int {
    slices.SortFunc(events, func(a, b []int) int { return a[1] - b[1] })
    n := len(events)
    f := make([][]int, n+1)
    for i := range f {
        f[i] = make([]int, k+1)
    }
    for i, e := range events {
        startDay, value := e[0], e[2]
        p := sort.Search(i, func(j int) bool { return events[j][1] >= startDay })
        for j := 1; j <= k; j++ {
            // 为什么是 p 不是 p+1：上面算的是 >= startDay，-1 后得到 < startDay，但由于还要 +1，抵消了
            f[i+1][j] = max(f[i][j], f[p][j-1]+value)
        }
    }
    return f[n][k]
}

var maxValue = function(events, k) {
    events.sort((a, b) => a[1] - b[1]);
    const n = events.length;
    const f = Array.from({ length: n + 1 }, () => Array(k + 1).fill(0));
    for (let i = 0; i < n; i++) {
        const p = search(events, i, events[i][0]);
        for (let j = 1; j <= k; j++) {
            f[i + 1][j] = Math.max(f[i][j], f[p + 1][j - 1] + events[i][2]);
        }
    }
    return f[n][k];
};

// 返回 endDay[i] < upper 的最大 i
var search = function(events, right, upper) {
    let left = -1;
    while (left + 1 < right) {
        const mid = (left + right) >>> 1;
        if (events[mid][1] < upper) {
            left = mid;
        } else {
            right = mid;
        }
    }
    return left;
};

impl Solution {
    pub fn max_value(mut events: Vec<Vec<i32>>, k: i32) -> i32 {
        events.sort_unstable_by_key(|a| a[1]);
        let n = events.len();
        let k = k as usize;
        let mut f = vec![vec![0; k + 1]; n + 1];
        for (i, e) in events.iter().enumerate() {
            let p = events[..i].partition_point(|a| a[1] < e[0]);
            for j in 1..=k {
                // 为什么是 p 不是 p+1：上面算的是 >= startDay，-1 后得到 < startDay，但由于还要 +1，抵消了
                f[i + 1][j] = f[i][j].max(f[p][j - 1] + e[2]);
            }
        }
        f[n][k]
    }
}

复杂度分析

时间复杂度：$\mathcal{O}(nk+n\log n)$，其中 $n$ 为 $\textit{events}$ 的长度。
空间复杂度：$\mathcal{O}(nk)$。

专题训练

见下面动态规划题单的「§7.2 不相交区间」。

分类题单

如何科学刷题？

我的题解精选（已分类）

欢迎关注 B站@灵茶山艾府

【宫水三叶】一题双解 :「朴素 DP」&「二分优化 DP」

LeetCode 每日一题题解

AC_OIer

2021年2月7日 12:26

基本思路

定义 $f[i][j]$ 为考虑前 $i$ 个事件，选择不超过 $j$ 的最大价值

对于每个事件，都有选择与不选两种选择：

不选： $f[i][j] = f[i - 1][j]$
选：找到第 $i$ 件事件之前，与第 $i$ 件事件不冲突的事件，记为 last，则有 $f[i][j] = f[last][j - 1] + value_i$

两者取 $max$，则是 $f[i][j]$ 的值。

分析到这里，因为我们要找 last，我们需要先对 events 的结束时间排序，然后找从右往左找，找到第一个满足 结束时间小于当前事件的开始时间 的事件，就是 last

而找 last 的过程，可以直接循环找，也可以通过二分来找，都能过。

动态规划

不通过「二分」来找 last 的 DP 解法。

代码：

###Java

class Solution {
    public int maxValue(int[][] es, int k) {
        int n = es.length;
        Arrays.sort(es, (a, b)->a[1]-b[1]);
        // f[i][j] 代表考虑前 i 个事件，选择不超过 j 的最大价值
        int[][] f = new int[n + 1][k + 1];
        for (int i = 1; i <= n; i++) {
            int[] ev = es[i - 1];
            int s = ev[0], e = ev[1], v = ev[2];
            
            // 找到第 i 件事件之前，与第 i 件事件不冲突的事件
            // 对于当前事件而言，冲突与否，与 j 无关
            int last = 0;
            for (int p = i - 1; p >= 1; p--) {
                int[] prev = es[p - 1];
                if (prev[1] < s) {
                    last = p;
                    break;
                }
            }
            
            for (int j = 1; j <= k; j++) {
                f[i][j] = Math.max(f[i - 1][j], f[last][j - 1] + v);    
            }
        }
        return f[n][k];
    }
}

时间复杂度：排序复杂度为 $O(n\log{n})$，循环 n 个事件，每次循环需要往回找一个事件，复杂度为 $O(n)$，并更新 k 个状态，复杂度为 $O(k)$，因此转移的复杂度为 $O(n * (n + k))$；总的复杂度为 $O(n * (n + k + \log{n}))$
空间复杂度：$O(n * k)$

二分 + 动态规划

通过「二分」来找 last 的 DP 解法。

代码：

###Java

class Solution {
    public int maxValue(int[][] es, int k) {
        int n = es.length;
        Arrays.sort(es, (a, b)->a[1]-b[1]);
        // f[i][j] 代表考虑前 i 个事件，选择不超过 j 的最大价值
        int[][] f = new int[n + 1][k + 1];
        for (int i = 1; i <= n; i++) {
            int[] ev = es[i - 1];
            int s = ev[0], e = ev[1], v = ev[2];
            
            // 通过「二分」，找到第 i 件事件之前，与第 i 件事件不冲突的事件
            // 对于当前事件而言，冲突与否，与 j 无关
            int l = 1, r = i - 1;
            while (l < r) {
                int mid = l + r + 1 >> 1;
                int[] prev = es[mid - 1];
                if (prev[1] < s) l = mid;    
                else r = mid - 1;
            }
            int last = (r > 0 && es[r - 1][1] < s) ? r : 0;
            
            for (int j = 1; j <= k; j++) {
                f[i][j] = Math.max(f[i - 1][j], f[last][j - 1] + v);    
            }
        }
        return f[n][k];
    }
}

时间复杂度：排序复杂度为 $O(n\log{n})$，循环 n 个事件，每次循环需要往回找一个事件，复杂度为 $O(\log{n})$，并更新 k 个状态，复杂度为 $O(k)$，因此转移的复杂度为 $O(n * (\log{n} + k))$；总的复杂度为 $O(n * (k + \log{n}))$
空间复杂度：$O(n * k)$

最后

如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ ("▔□▔)/

也欢迎你关注我和加入我们的「组队打卡」小群，提供写「证明」&「思路」的高质量题解。

所有题解已经加入刷题指南，欢迎 star 哦 ~

【动态规划 + 二分搜索】最多可以参加的会议数目

LeetCode 每日一题题解

Arsenal-591

2021年2月7日 00:09

首先将每个会议按照结束时间排序。

设 $\textit{dp}[i][k]$ 为：参加前 $i$ 个会议中的恰好 $k$ 个时，所能获得的最大会议价值。

对于 $\textit{dp}[i][k]$ 而言，若要参加前 $i$ 个会议中的 $k$ 个：

要么不参加第 $i$ 个会议。此时需要在前 $i-1$ 个会议中参加 $k$ 个，能够获得的最大价值为 $\textit{dp}[i-1][k]$；
要么参加第 $i$ 个会议。此时任何 $\textit{endDay}$ 不小于 第 $i$ 个会议的开始时间那些会议，都会因为时间重合而无法参加。

对于第二种情况而言，由于会议已经事先按照结束时间排序，故不妨设 $l$ 为满足「结束时间小于第 $i$ 个会议的开始时间」的最后一个会议。此时，我们需要在前 $l$ 个会议中选择 $k-1$ 个，对应的价值为 $\textit{dp}[l][k-1] + \textit{value}[i]$。在排序好的数组中，通过二分搜索，就能够快速地找到 $l$ 的值。

另外，还要额外考虑不存在 $l$ 的情形，即「若参加第 $i$ 个会议，则此前所有的会议都无法参加」。

class Solution {
public:
    static bool cmp(const vector<int>& x, const vector<int>& y) {
        return x[1] < y[1];
    }
    int maxValue(vector<vector<int>>& events, int k) {
        int n = events.size();
        sort(events.begin(), events.end(), cmp);
        
        vector<vector<int>> dp(n, vector<int>(k + 1, INT_MIN));
        dp[0][0] = 0;
        dp[0][1] = events[0][2];
        
        for (int i = 1; i < n; i++) {
            // 参加会议 i，此时需要二分查找
            int l = 0, r = i;
            while (r - l > 1) {
                int mid = (l + r) / 2;
                if (events[mid][1] >= events[i][0]) {
                    r = mid;
                } else {
                    l = mid;
                }
            }
            if (events[l][1] < events[i][0]) {
                for (int j = 1; j <= k; j++) {
                    dp[i][j] = max(dp[i][j], dp[l][j-1] + events[i][2]);
                }
            } else {
                dp[i][1] = max(dp[i][1], events[i][2]);
            }
            
            // 不参加会议 i
            for (int j = 0; j <= k; j++) {
                dp[i][j] = max(dp[i][j], dp[i-1][j]);
            }
        }
        
        int ret = 0;
        for (int i = 0; i <= k; i++) {
            ret = max(ret, dp[n-1][i]);
        }
        return ret;
    }
};

复杂度分析

时间复杂度：$O(n\log n + nk)$。排序部分需要 $O(n\log n)$ 的复杂度。对于单个 $i$ 而言，二分查找的时间为 $O(\log n)$，更新 $\textit{dp}$ 数组的时间为 $O(k)$。因此，总的复杂度为 $O(n\log n) + O(n \cdot (\log n + k)) = O(n\log n + nk)$。
空间复杂度：$O(nk)$。